Question Number 111024 by mathmax by abdo last updated on 01/Sep/20
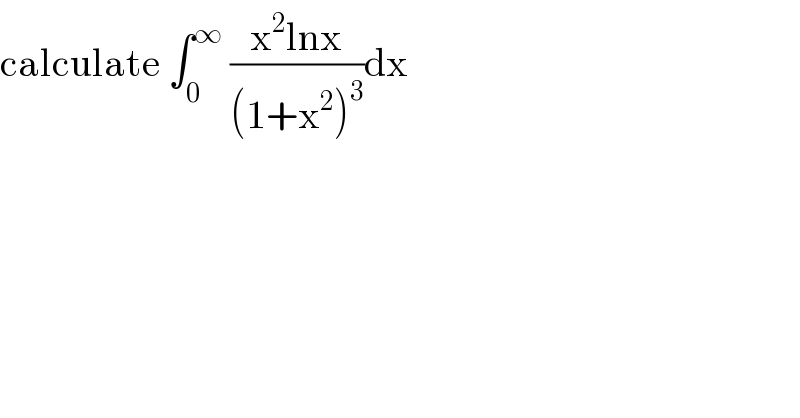
$$\mathrm{calculate}\:\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{x}^{\mathrm{2}} \mathrm{lnx}}{\left(\mathrm{1}+\mathrm{x}^{\mathrm{2}} \right)^{\mathrm{3}} }\mathrm{dx} \\ $$
Answered by mathdave last updated on 01/Sep/20
![solution let I=∫_0 ^∞ ((x^2 lnx)/((1+x^2 )^3 ))dx then (∂/∂a)∣_(a=0) I(a)=(1/4)(∂/∂a)∫_0 ^∞ (x^((1/2)+a) /((1+x)^3 ))dx I^1 (a)=(1/4)(∂/∂a)β((3/2)+a,(3/2)−a)=(1/4)(∂/∂a)[((Γ((3/2)+a)Γ((3/2)−a))/(Γ(3)))] I^′ (0)=(1/4)•((Γ((3/2))Γ((3/2)))/(Γ(3)))[ψ((3/2))−ψ((3/2))]=0 ∫_0 ^∞ ((x^2 lnx)/((1+x^2 )^3 ))dx=0 mathdave(01/09/2020)](https://www.tinkutara.com/question/Q111037.png)
$${solution} \\ $$$${let}\:{I}=\int_{\mathrm{0}} ^{\infty} \frac{{x}^{\mathrm{2}} \mathrm{ln}{x}}{\left(\mathrm{1}+{x}^{\mathrm{2}} \right)^{\mathrm{3}} }{dx}\:\:{then} \\ $$$$\frac{\partial}{\partial{a}}\mid_{{a}=\mathrm{0}} {I}\left({a}\right)=\frac{\mathrm{1}}{\mathrm{4}}\frac{\partial}{\partial{a}}\int_{\mathrm{0}} ^{\infty} \frac{{x}^{\frac{\mathrm{1}}{\mathrm{2}}+{a}} }{\left(\mathrm{1}+{x}\right)^{\mathrm{3}} }{dx} \\ $$$${I}^{\mathrm{1}} \left({a}\right)=\frac{\mathrm{1}}{\mathrm{4}}\frac{\partial}{\partial{a}}\beta\left(\frac{\mathrm{3}}{\mathrm{2}}+{a},\frac{\mathrm{3}}{\mathrm{2}}−{a}\right)=\frac{\mathrm{1}}{\mathrm{4}}\frac{\partial}{\partial{a}}\left[\frac{\Gamma\left(\frac{\mathrm{3}}{\mathrm{2}}+{a}\right)\Gamma\left(\frac{\mathrm{3}}{\mathrm{2}}−{a}\right)}{\Gamma\left(\mathrm{3}\right)}\right] \\ $$$${I}^{'} \left(\mathrm{0}\right)=\frac{\mathrm{1}}{\mathrm{4}}\bullet\frac{\Gamma\left(\frac{\mathrm{3}}{\mathrm{2}}\right)\Gamma\left(\frac{\mathrm{3}}{\mathrm{2}}\right)}{\Gamma\left(\mathrm{3}\right)}\left[\psi\left(\frac{\mathrm{3}}{\mathrm{2}}\right)−\psi\left(\frac{\mathrm{3}}{\mathrm{2}}\right)\right]=\mathrm{0} \\ $$$$\int_{\mathrm{0}} ^{\infty} \frac{{x}^{\mathrm{2}} \mathrm{ln}{x}}{\left(\mathrm{1}+{x}^{\mathrm{2}} \right)^{\mathrm{3}} }{dx}=\mathrm{0} \\ $$$${mathdave}\left(\mathrm{01}/\mathrm{09}/\mathrm{2020}\right) \\ $$$$ \\ $$
Commented by abdomsup last updated on 01/Sep/20

$${thank}\:{you} \\ $$
