Question Number 166956 by mnjuly1970 last updated on 03/Mar/22
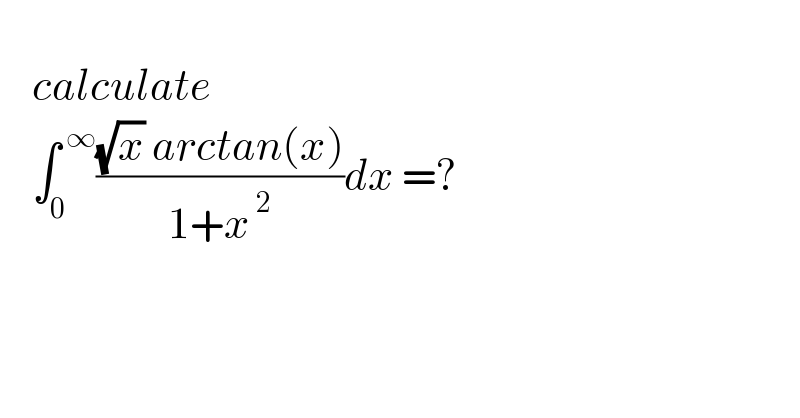
$$ \\ $$$$\:\:\:\:{calculate} \\ $$$$\:\:\:\:\int_{\mathrm{0}} ^{\:\infty} \frac{\sqrt{{x}}\:{arctan}\left({x}\right)}{\mathrm{1}+{x}^{\:\mathrm{2}} }{dx}\:=? \\ $$
Answered by ArielVyny last updated on 03/Mar/22
![dt=((arctan(x))/(1+x^2 ))dx→t=(1/2)(arctanx)^2 (√(2t))=arctanx→x=arctan((√2)t) ∫_0 ^(π^2 /( 8)) arctan((√2)t)dt= (1/( (√2)))∫_0 ^(π^2 /8) arctan(u)du we cant stop here =Σ_(n≥0) (((−1)^n ((√2))^(2n+1) )/(2n+1))∫_0 ^(π^2 /8) t^(2n+1) dt =Σ_(n≥0) (((−1)^n ((√2))^(2n+1) )/(2n+1))[(1/(2n+2))(π^2 /8)] =(π^2 /8)Σ_(n≥0) (((−1)^n ((√2))^(2n+1) )/((2n+1)(2n+2))) =(π^2 /8)[Σ(((−1)^n ((√2))^(2n+1) )/(2n+1))]−(π^2 /8)Σ_(n≥0) (((−1)^n ((√2))^(2n+1) )/(2n+2)) =(π^2 /8)arctan((√2))(π^2 /(16))Σ_(n≥1) (((−1)^(n+1) (2)^n )/n) =(π^2 /8)arctan((√2))+(π^2 /(16))ln(3)](https://www.tinkutara.com/question/Q166969.png)
$${dt}=\frac{{arctan}\left({x}\right)}{\mathrm{1}+{x}^{\mathrm{2}} }{dx}\rightarrow{t}=\frac{\mathrm{1}}{\mathrm{2}}\left({arctanx}\right)^{\mathrm{2}} \\ $$$$\sqrt{\mathrm{2}{t}}={arctanx}\rightarrow{x}={arctan}\left(\sqrt{\mathrm{2}}{t}\right) \\ $$$$\int_{\mathrm{0}} ^{\frac{\pi^{\mathrm{2}} }{\:\mathrm{8}}} {arctan}\left(\sqrt{\mathrm{2}}{t}\right){dt}= \\ $$$$\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\int_{\mathrm{0}} ^{\frac{\pi^{\mathrm{2}} }{\mathrm{8}}} {arctan}\left({u}\right){du}\: \\ $$$${we}\:{cant}\:{stop}\:{here}\: \\ $$$$=\underset{{n}\geqslant\mathrm{0}} {\sum}\frac{\left(−\mathrm{1}\right)^{{n}} \left(\sqrt{\mathrm{2}}\right)^{\mathrm{2}{n}+\mathrm{1}} }{\mathrm{2}{n}+\mathrm{1}}\int_{\mathrm{0}} ^{\frac{\pi^{\mathrm{2}} }{\mathrm{8}}} {t}^{\mathrm{2}{n}+\mathrm{1}} {dt} \\ $$$$=\underset{{n}\geqslant\mathrm{0}} {\sum}\frac{\left(−\mathrm{1}\right)^{{n}} \left(\sqrt{\mathrm{2}}\right)^{\mathrm{2}{n}+\mathrm{1}} }{\mathrm{2}{n}+\mathrm{1}}\left[\frac{\mathrm{1}}{\mathrm{2}{n}+\mathrm{2}}\frac{\pi^{\mathrm{2}} }{\mathrm{8}}\right] \\ $$$$=\frac{\pi^{\mathrm{2}} }{\mathrm{8}}\underset{{n}\geqslant\mathrm{0}} {\sum}\frac{\left(−\mathrm{1}\right)^{{n}} \left(\sqrt{\mathrm{2}}\right)^{\mathrm{2}{n}+\mathrm{1}} }{\left(\mathrm{2}{n}+\mathrm{1}\right)\left(\mathrm{2}{n}+\mathrm{2}\right)} \\ $$$$=\frac{\pi^{\mathrm{2}} }{\mathrm{8}}\left[\Sigma\frac{\left(−\mathrm{1}\right)^{{n}} \left(\sqrt{\mathrm{2}}\right)^{\mathrm{2}{n}+\mathrm{1}} }{\mathrm{2}{n}+\mathrm{1}}\right]−\frac{\pi^{\mathrm{2}} }{\mathrm{8}}\underset{{n}\geqslant\mathrm{0}} {\sum}\frac{\left(−\mathrm{1}\right)^{{n}} \left(\sqrt{\mathrm{2}}\right)^{\mathrm{2}{n}+\mathrm{1}} }{\mathrm{2}{n}+\mathrm{2}} \\ $$$$=\frac{\pi^{\mathrm{2}} }{\mathrm{8}}{arctan}\left(\sqrt{\mathrm{2}}\right)\frac{\pi^{\mathrm{2}} }{\mathrm{16}}\underset{{n}\geqslant\mathrm{1}} {\sum}\frac{\left(−\mathrm{1}\right)^{{n}+\mathrm{1}} \left(\mathrm{2}\right)^{{n}} }{{n}} \\ $$$$=\frac{\pi^{\mathrm{2}} }{\mathrm{8}}{arctan}\left(\sqrt{\mathrm{2}}\right)+\frac{\pi^{\mathrm{2}} }{\mathrm{16}}{ln}\left(\mathrm{3}\right) \\ $$$$ \\ $$
