Question Number 64904 by mathmax by abdo last updated on 23/Jul/19
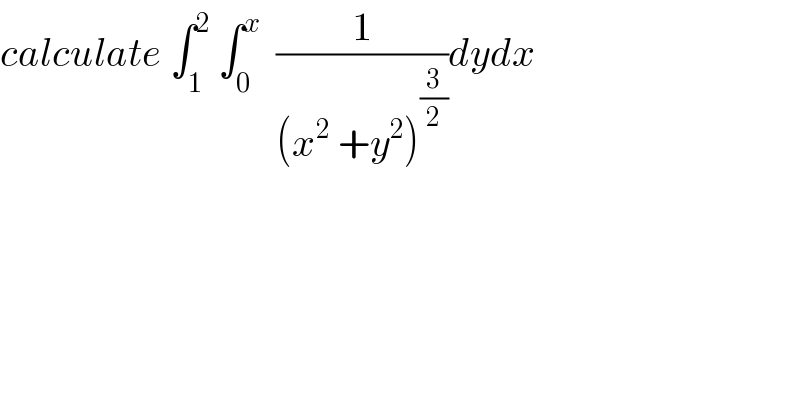
$${calculate}\:\int_{\mathrm{1}} ^{\mathrm{2}} \:\int_{\mathrm{0}} ^{{x}} \:\:\frac{\mathrm{1}}{\left({x}^{\mathrm{2}} \:+{y}^{\mathrm{2}} \right)^{\frac{\mathrm{3}}{\mathrm{2}}} }{dydx}\: \\ $$
Commented by ~ À ® @ 237 ~ last updated on 23/Jul/19
![le domaine d integration D ={(x . y) / 1<x<2 0<y<x} en posant x=u et y=utanv on a J(x y)=utanv(1+tan^2 v) D={(u. utanv)/ 1<u<2 et 0<tanv<1} ={(u. utanv)/ 1<u<2 et 0<v<(π/4) } on obtient alors I= ∫_1 ^2 ∫_0 ^(π/4) ((utanv(1+tan^2 v)dudv)/(((√((u^2 +u^2 tan^2 v))))^3 )) =∫_1 ^2 (1/u^2 )du ∫_0 ^(π/4) ((tanv(1+tan^2 v)dv)/((1+tan^2 v)^(3/2) )) =[−(1/u)]_1 ^2 [(1/2) ((−1)/(((3/2)−1)(1+tan^2 v)^(((3/2)−1)) ))]_0 ^(π/4) = = (((2−(√2)))/4)](https://www.tinkutara.com/question/Q64976.png)
$${le}\:{domaine}\:{d}\:{integration}\:{D}\:=\left\{\left({x}\:.\:\:{y}\right)\:\:/\:\mathrm{1}<{x}<\mathrm{2}\:\:\:\:\mathrm{0}<{y}<{x}\right\} \\ $$$${en}\:{posant}\:{x}={u}\:{et}\:{y}={utanv}\:\:\:\:\:{on}\:{a}\:{J}\left({x}\:\:{y}\right)={utanv}\left(\mathrm{1}+{tan}^{\mathrm{2}} {v}\right) \\ $$$${D}=\left\{\left({u}.\:{utanv}\right)/\:\mathrm{1}<{u}<\mathrm{2}\:\:{et}\:\mathrm{0}<{tanv}<\mathrm{1}\right\} \\ $$$$\:\:\:=\left\{\left({u}.\:{utanv}\right)/\:\:\mathrm{1}<{u}<\mathrm{2}\:{et}\:\mathrm{0}<{v}<\frac{\pi}{\mathrm{4}}\:\right\} \\ $$$${on}\:{obtient}\:{alors}\: \\ $$$${I}=\:\int_{\mathrm{1}} ^{\mathrm{2}} \int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \:\frac{{utanv}\left(\mathrm{1}+{tan}^{\mathrm{2}} {v}\right){dudv}}{\left(\sqrt{\left({u}^{\mathrm{2}} +{u}^{\mathrm{2}} {tan}^{\mathrm{2}} {v}\right)}\right)^{\mathrm{3}} } \\ $$$$\:\:=\int_{\mathrm{1}} ^{\mathrm{2}} \frac{\mathrm{1}}{{u}^{\mathrm{2}} }{du}\:\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \frac{{tanv}\left(\mathrm{1}+{tan}^{\mathrm{2}} {v}\right){dv}}{\left(\mathrm{1}+{tan}^{\mathrm{2}} {v}\right)^{\frac{\mathrm{3}}{\mathrm{2}}} } \\ $$$$\:\:=\left[−\frac{\mathrm{1}}{{u}}\right]_{\mathrm{1}} ^{\mathrm{2}} \:\left[\frac{\mathrm{1}}{\mathrm{2}}\:\frac{−\mathrm{1}}{\left(\frac{\mathrm{3}}{\mathrm{2}}−\mathrm{1}\right)\left(\mathrm{1}+{tan}^{\mathrm{2}} {v}\right)^{\left(\frac{\mathrm{3}}{\mathrm{2}}−\mathrm{1}\right)} }\overset{\frac{\pi}{\mathrm{4}}} {\right]}_{\mathrm{0}} \\ $$$$= \\ $$$$=\:\frac{\left(\mathrm{2}−\sqrt{\mathrm{2}}\right)}{\mathrm{4}} \\ $$
Commented by mathmax by abdo last updated on 23/Jul/19

$${thank}\:{you}\:{sir}. \\ $$
