Question Number 51990 by maxmathsup by imad last updated on 01/Jan/19
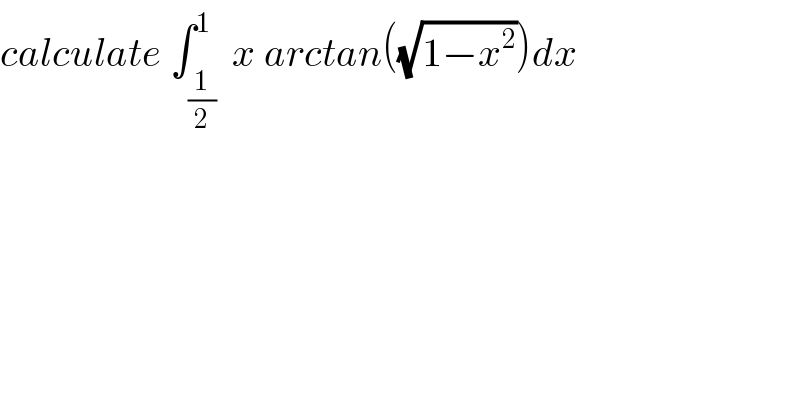
$${calculate}\:\int_{\frac{\mathrm{1}}{\mathrm{2}}} ^{\mathrm{1}} \:{x}\:{arctan}\left(\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }\right){dx} \\ $$
Answered by peter frank last updated on 01/Jan/19
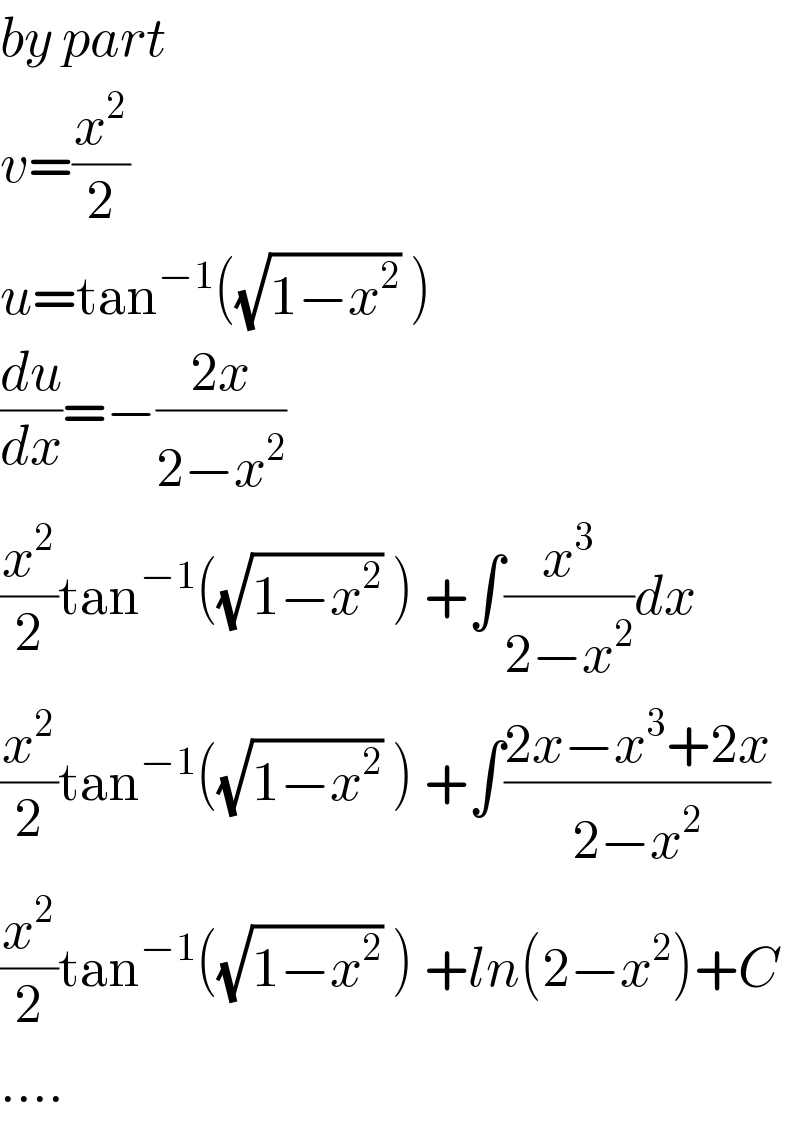
$${by}\:{part} \\ $$$${v}=\frac{{x}^{\mathrm{2}} }{\mathrm{2}} \\ $$$${u}=\mathrm{tan}^{−\mathrm{1}} \left(\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }\:\right) \\ $$$$\frac{{du}}{{dx}}=−\frac{\mathrm{2}{x}}{\mathrm{2}−{x}^{\mathrm{2}} } \\ $$$$\frac{{x}^{\mathrm{2}} }{\mathrm{2}}\mathrm{tan}^{−\mathrm{1}} \left(\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }\:\right)\:+\int\frac{{x}^{\mathrm{3}} }{\mathrm{2}−{x}^{\mathrm{2}} }{dx} \\ $$$$\frac{{x}^{\mathrm{2}} }{\mathrm{2}}\mathrm{tan}^{−\mathrm{1}} \left(\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }\:\right)\:+\int\frac{\mathrm{2}{x}−{x}^{\mathrm{3}} +\mathrm{2}{x}}{\mathrm{2}−{x}^{\mathrm{2}} } \\ $$$$\frac{{x}^{\mathrm{2}} }{\mathrm{2}}\mathrm{tan}^{−\mathrm{1}} \left(\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }\:\right)\:+{ln}\left(\mathrm{2}−{x}^{\mathrm{2}} \right)+{C} \\ $$$$…. \\ $$
