Question Number 43675 by maxmathsup by imad last updated on 13/Sep/18
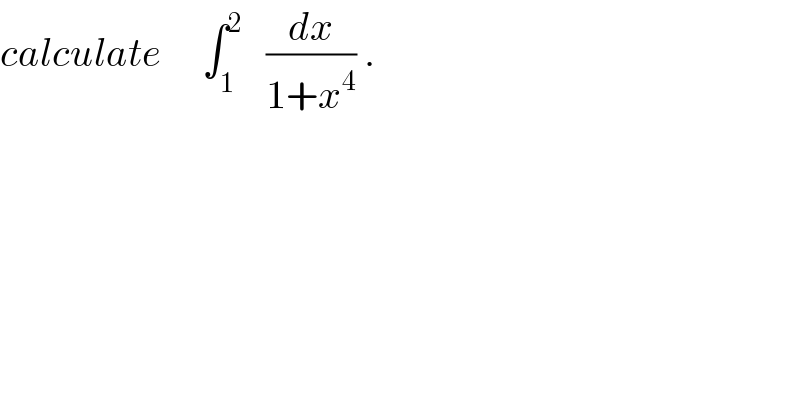
$${calculate}\:\:\:\:\:\int_{\mathrm{1}} ^{\mathrm{2}} \:\:\:\frac{{dx}}{\mathrm{1}+{x}^{\mathrm{4}} }\:. \\ $$
Commented by maxmathsup by imad last updated on 15/Sep/18
![we have proved that ∫ (dx/(1+x^4 )) =(1/(4(√2)))ln∣((x^2 −(√2)x+1)/(x^2 +(√2)x+1))∣ +(1/(2(√2))){ arctan(x(√2)−1)+arctan(x(√2)+1)} ⇒ ∫_1 ^2 (dx/(1+x^4 )) =(1/(4(√2)))[ln∣((x^2 −(√2)x +1)/(x^2 +(√2)x+1))∣_1 ^2 +(1/(2(√2)))[arctan(x(√2)−1)+arctan(x(√2)+1)]_1 ^2 =(1/(4(√2))){ln(((5−2(√2))/(5+2(√2))))−ln(((2−(√2))/(2+(√2))))}+(1/(2(√2))){arctan(2(√2)−1)+arctan(2(√2)+1) −arctan((√2)−1)−arctan((√2) +1)} .](https://www.tinkutara.com/question/Q43813.png)
$${we}\:{have}\:{proved}\:{that}\: \\ $$$$\int\:\frac{{dx}}{\mathrm{1}+{x}^{\mathrm{4}} }\:=\frac{\mathrm{1}}{\mathrm{4}\sqrt{\mathrm{2}}}{ln}\mid\frac{{x}^{\mathrm{2}} −\sqrt{\mathrm{2}}{x}+\mathrm{1}}{{x}^{\mathrm{2}} \:+\sqrt{\mathrm{2}}{x}+\mathrm{1}}\mid\:+\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{2}}}\left\{\:{arctan}\left({x}\sqrt{\mathrm{2}}−\mathrm{1}\right)+{arctan}\left({x}\sqrt{\mathrm{2}}+\mathrm{1}\right)\right\}\:\Rightarrow \\ $$$$\int_{\mathrm{1}} ^{\mathrm{2}} \:\:\frac{{dx}}{\mathrm{1}+{x}^{\mathrm{4}} }\:=\frac{\mathrm{1}}{\mathrm{4}\sqrt{\mathrm{2}}}\left[{ln}\mid\frac{{x}^{\mathrm{2}} −\sqrt{\mathrm{2}}{x}\:+\mathrm{1}}{{x}^{\mathrm{2}} \:+\sqrt{\mathrm{2}}{x}+\mathrm{1}}\mid_{\mathrm{1}} ^{\mathrm{2}} \:+\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{2}}}\left[{arctan}\left({x}\sqrt{\mathrm{2}}−\mathrm{1}\right)+{arctan}\left({x}\sqrt{\mathrm{2}}+\mathrm{1}\right)\right]_{\mathrm{1}} ^{\mathrm{2}} \right. \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}\sqrt{\mathrm{2}}}\left\{{ln}\left(\frac{\mathrm{5}−\mathrm{2}\sqrt{\mathrm{2}}}{\mathrm{5}+\mathrm{2}\sqrt{\mathrm{2}}}\right)−{ln}\left(\frac{\mathrm{2}−\sqrt{\mathrm{2}}}{\mathrm{2}+\sqrt{\mathrm{2}}}\right)\right\}+\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{2}}}\left\{{arctan}\left(\mathrm{2}\sqrt{\mathrm{2}}−\mathrm{1}\right)+{arctan}\left(\mathrm{2}\sqrt{\mathrm{2}}+\mathrm{1}\right)\right. \\ $$$$\left.−{arctan}\left(\sqrt{\mathrm{2}}−\mathrm{1}\right)−{arctan}\left(\sqrt{\mathrm{2}}\:+\mathrm{1}\right)\right\}\:. \\ $$
