Question Number 115366 by Bird last updated on 25/Sep/20

$${calculate}\:\int_{−\mathrm{1}} ^{\mathrm{2}} \:\frac{{dx}}{{ch}^{\mathrm{2}} {x}\:+{sh}^{\mathrm{2}} {x}} \\ $$
Answered by MJS_new last updated on 25/Sep/20
![∫(dx/(cosh^2 x +sinh^2 x))= [t=e^(2x) → dx=(dt/(2e^(2x) ))] =∫(dt/(t^2 +1))=arctan t = =arctan e^(2x) +C ∫_(−1) ^2 (dx/(cosh^2 x +sinh^2 x))=arctan e^4 −arctan e^(−2)](https://www.tinkutara.com/question/Q115379.png)
$$\int\frac{{dx}}{\mathrm{cosh}^{\mathrm{2}} \:{x}\:+\mathrm{sinh}^{\mathrm{2}} \:{x}}= \\ $$$$\:\:\:\:\:\left[{t}=\mathrm{e}^{\mathrm{2}{x}} \:\rightarrow\:{dx}=\frac{{dt}}{\mathrm{2e}^{\mathrm{2}{x}} }\right] \\ $$$$=\int\frac{{dt}}{{t}^{\mathrm{2}} +\mathrm{1}}=\mathrm{arctan}\:{t}\:= \\ $$$$=\mathrm{arctan}\:\mathrm{e}^{\mathrm{2}{x}} \:+{C} \\ $$$$\underset{−\mathrm{1}} {\overset{\mathrm{2}} {\int}}\frac{{dx}}{\mathrm{cosh}^{\mathrm{2}} \:{x}\:+\mathrm{sinh}^{\mathrm{2}} \:{x}}=\mathrm{arctan}\:\mathrm{e}^{\mathrm{4}} \:−\mathrm{arctan}\:\mathrm{e}^{−\mathrm{2}} \\ $$
Commented by mathmax by abdo last updated on 25/Sep/20

$$\mathrm{thank}\:\mathrm{you}\:\mathrm{sir}\:\mathrm{mjs} \\ $$
Answered by mathmax by abdo last updated on 25/Sep/20
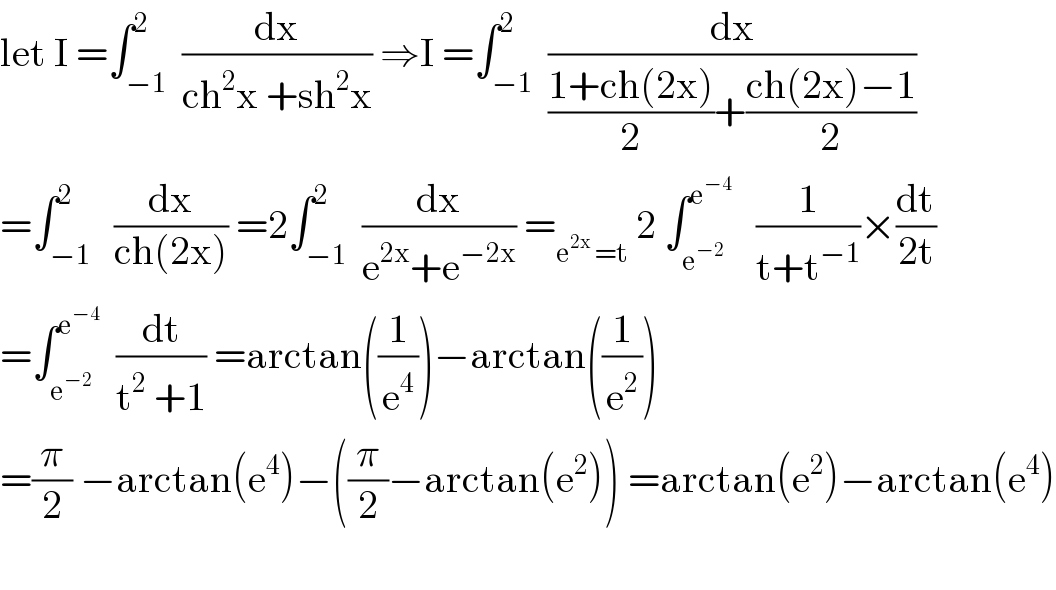
$$\mathrm{let}\:\mathrm{I}\:=\int_{−\mathrm{1}} ^{\mathrm{2}} \:\frac{\mathrm{dx}}{\mathrm{ch}^{\mathrm{2}} \mathrm{x}\:+\mathrm{sh}^{\mathrm{2}} \mathrm{x}}\:\Rightarrow\mathrm{I}\:=\int_{−\mathrm{1}} ^{\mathrm{2}} \:\frac{\mathrm{dx}}{\frac{\mathrm{1}+\mathrm{ch}\left(\mathrm{2x}\right)}{\mathrm{2}}+\frac{\mathrm{ch}\left(\mathrm{2x}\right)−\mathrm{1}}{\mathrm{2}}} \\ $$$$=\int_{−\mathrm{1}} ^{\mathrm{2}} \:\:\frac{\mathrm{dx}}{\mathrm{ch}\left(\mathrm{2x}\right)}\:=\mathrm{2}\int_{−\mathrm{1}} ^{\mathrm{2}} \:\frac{\mathrm{dx}}{\mathrm{e}^{\mathrm{2x}} +\mathrm{e}^{−\mathrm{2x}} }\:=_{\mathrm{e}^{\mathrm{2x}} \:=\mathrm{t}} \:\mathrm{2}\:\int_{\mathrm{e}^{−\mathrm{2}} } ^{\mathrm{e}^{−\mathrm{4}} } \:\:\:\frac{\mathrm{1}}{\mathrm{t}+\mathrm{t}^{−\mathrm{1}} }×\frac{\mathrm{dt}}{\mathrm{2t}} \\ $$$$=\int_{\mathrm{e}^{−\mathrm{2}} } ^{\mathrm{e}^{−\mathrm{4}} } \:\:\frac{\mathrm{dt}}{\mathrm{t}^{\mathrm{2}} \:+\mathrm{1}}\:=\mathrm{arctan}\left(\frac{\mathrm{1}}{\mathrm{e}^{\mathrm{4}} }\right)−\mathrm{arctan}\left(\frac{\mathrm{1}}{\mathrm{e}^{\mathrm{2}} }\right) \\ $$$$=\frac{\pi}{\mathrm{2}}\:−\mathrm{arctan}\left(\mathrm{e}^{\mathrm{4}} \right)−\left(\frac{\pi}{\mathrm{2}}−\mathrm{arctan}\left(\mathrm{e}^{\mathrm{2}} \right)\right)\:=\mathrm{arctan}\left(\mathrm{e}^{\mathrm{2}} \right)−\mathrm{arctan}\left(\mathrm{e}^{\mathrm{4}} \right) \\ $$$$ \\ $$
