Question Number 36754 by prof Abdo imad last updated on 05/Jun/18

$${calculate}\:\:\:\int_{\mathrm{1}} ^{+\infty} \:\:\:\:\frac{{dx}}{{x}^{\mathrm{2}} \sqrt{\mathrm{4}+{x}^{\mathrm{2}} }}\:. \\ $$
Commented by abdo mathsup 649 cc last updated on 05/Jun/18
![changement x=2 sh(t) give I = ∫_(argsh((1/2))) ^(+∞) (1/(4 sh^2 t.2cht)) ((2ch(t)dt)/) =(1/4) ∫_(argsh((1/2))) ^(+∞) (dt/((ch(2t)−1)/2)) = (1/2) ∫_(argsh((1/2))) ^(+∞) (dt/( ((e^(2t) +e^(−2t) )/2)−1)) = ∫_(argsh((1/2))) ^(+∞) (dt/(e^(2t) +e^(−2t) −2))=∫_(ln((1/2) +((√5)/2))) ^(+∞) (dt/(e^(2t) +e^(−2t) −2)) =_(e^(2t) =u) ∫_(((1/2)+((√5)/2))^2 ) ^(+∞) (1/(u +(1/u) −2))(du/(2u)) = (1/2)∫_((6+2(√5))/4) ^(+∞) (du/(u^2 +1)) =(1/2)[ arctanu]_((6+2(√5))/4) ^(+∞) =(π/4) −(1/2) arctan( ((6+2(√5))/4)) .](https://www.tinkutara.com/question/Q36785.png)
$${changement}\:\:{x}=\mathrm{2}\:{sh}\left({t}\right)\:{give} \\ $$$${I}\:=\:\int_{{argsh}\left(\frac{\mathrm{1}}{\mathrm{2}}\right)} ^{+\infty} \:\:\:\:\frac{\mathrm{1}}{\mathrm{4}\:{sh}^{\mathrm{2}} {t}.\mathrm{2}{cht}}\:\frac{\mathrm{2}{ch}\left({t}\right){dt}}{} \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}}\:\int_{{argsh}\left(\frac{\mathrm{1}}{\mathrm{2}}\right)} ^{+\infty} \:\:\:\frac{{dt}}{\frac{{ch}\left(\mathrm{2}{t}\right)−\mathrm{1}}{\mathrm{2}}} \\ $$$$=\:\frac{\mathrm{1}}{\mathrm{2}}\:\int_{{argsh}\left(\frac{\mathrm{1}}{\mathrm{2}}\right)} ^{+\infty} \:\:\:\frac{{dt}}{\:\frac{{e}^{\mathrm{2}{t}} \:+{e}^{−\mathrm{2}{t}} }{\mathrm{2}}−\mathrm{1}} \\ $$$$=\:\int_{{argsh}\left(\frac{\mathrm{1}}{\mathrm{2}}\right)} ^{+\infty} \:\:\:\:\frac{{dt}}{{e}^{\mathrm{2}{t}} \:+{e}^{−\mathrm{2}{t}} \:−\mathrm{2}}=\int_{{ln}\left(\frac{\mathrm{1}}{\mathrm{2}}\:+\frac{\sqrt{\mathrm{5}}}{\mathrm{2}}\right)} ^{+\infty} \:\:\:\frac{{dt}}{{e}^{\mathrm{2}{t}} \:+{e}^{−\mathrm{2}{t}} \:−\mathrm{2}} \\ $$$$=_{{e}^{\mathrm{2}{t}} \:={u}} \:\:\:\:\int_{\left(\frac{\mathrm{1}}{\mathrm{2}}+\frac{\sqrt{\mathrm{5}}}{\mathrm{2}}\right)^{\mathrm{2}} } ^{+\infty} \:\:\:\:\:\:\:\:\:\frac{\mathrm{1}}{{u}\:+\frac{\mathrm{1}}{{u}}\:−\mathrm{2}}\frac{{du}}{\mathrm{2}{u}} \\ $$$$=\:\frac{\mathrm{1}}{\mathrm{2}}\int_{\frac{\mathrm{6}+\mathrm{2}\sqrt{\mathrm{5}}}{\mathrm{4}}} ^{+\infty} \:\:\:\:\:\frac{{du}}{{u}^{\mathrm{2}} \:+\mathrm{1}}\:=\frac{\mathrm{1}}{\mathrm{2}}\left[\:{arctanu}\right]_{\frac{\mathrm{6}+\mathrm{2}\sqrt{\mathrm{5}}}{\mathrm{4}}} ^{+\infty} \\ $$$$=\frac{\pi}{\mathrm{4}}\:−\frac{\mathrm{1}}{\mathrm{2}}\:{arctan}\left(\:\frac{\mathrm{6}+\mathrm{2}\sqrt{\mathrm{5}}}{\mathrm{4}}\right)\:. \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 05/Jun/18
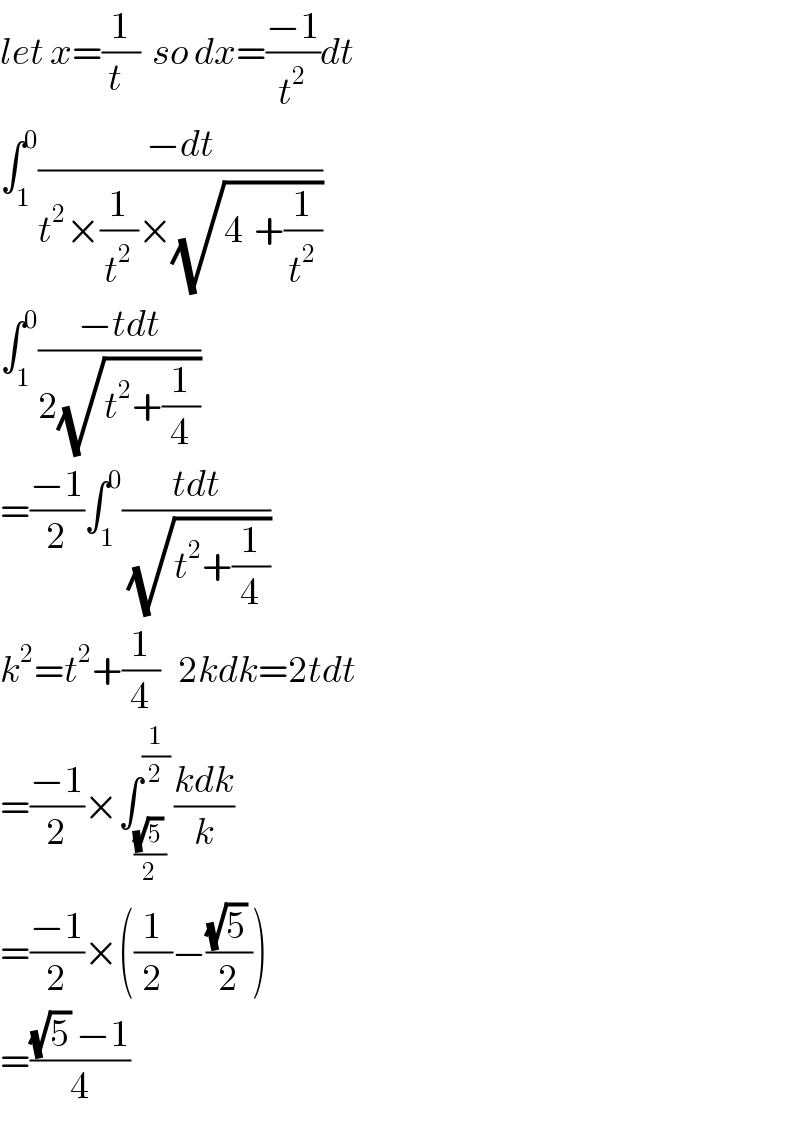
$${let}\:{x}=\frac{\mathrm{1}}{{t}\:\:}\:\:{so}\:{dx}=\frac{−\mathrm{1}}{{t}^{\mathrm{2}} }{dt} \\ $$$$\int_{\mathrm{1}} ^{\mathrm{0}} \frac{−{dt}}{{t}^{\mathrm{2}} ×\frac{\mathrm{1}}{{t}^{\mathrm{2}} }×\sqrt{\mathrm{4}_{} +\frac{\mathrm{1}}{{t}^{\mathrm{2}} }}} \\ $$$$\int_{\mathrm{1}} ^{\mathrm{0}} \frac{−{tdt}}{\mathrm{2}\sqrt{{t}^{\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{4}}}} \\ $$$$=\frac{−\mathrm{1}}{\mathrm{2}}\int_{\mathrm{1}} ^{\mathrm{0}} \frac{{tdt}}{\:\sqrt{{t}^{\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{4}}}} \\ $$$${k}^{\mathrm{2}} ={t}^{\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{4}}\:\:\:\mathrm{2}{kdk}=\mathrm{2}{tdt} \\ $$$$=\frac{−\mathrm{1}}{\mathrm{2}}×\int_{\frac{\sqrt{\mathrm{5}}\:}{\mathrm{2}}} ^{\frac{\mathrm{1}}{\mathrm{2}}} \frac{{kdk}}{{k}} \\ $$$$=\frac{−\mathrm{1}}{\mathrm{2}}×\left(\frac{\mathrm{1}}{\mathrm{2}}−\frac{\sqrt{\mathrm{5}}\:}{\mathrm{2}}\right) \\ $$$$=\frac{\sqrt{\mathrm{5}}\:−\mathrm{1}}{\mathrm{4}} \\ $$
