Menu Close

calculate-1-dx-x-3-2-x-2-

Tinku Tara 0 Comments
Pin




Question Number 43905 by abdo.msup.com last updated on 17/Sep/18
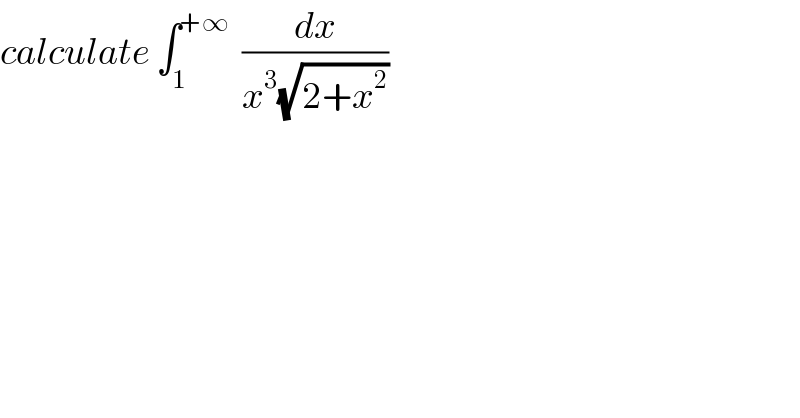
calculate ∫_1 ^(+∞) (dx/(x^3 (√(2+x^2 ))))
$${calculate}\:\int_{\mathrm{1}} ^{+\infty} \:\:\frac{{dx}}{{x}^{\mathrm{3}} \sqrt{\mathrm{2}+{x}^{\mathrm{2}} }} \\ $$
Commented by maxmathsup by imad last updated on 18/Sep/18
let A = ∫_1 ^(+∞) (dx/(x^3 (√(2+x^2 ))))dx changement x =(√2)sh(t) give A = ∫_(argsh((1/( (√2))))) ^(+∞) (((√2)ch(t)dt)/(2(√2)sh^3 (t)(√2)ch(t))) =(1/(2(√2))) ∫_(ln((1/( (√2) ))+(√(3/2)))) ^(+∞) (dt/((((e^t −e^(−t) )/2))^3 )) =(4/( (√2))) ∫_(ln((1/( (√2)))+((√3)/( (√2))))) ^(+∞) (dt/(e^(3t) +3 e^(2t) e^(−t) +3 e^t e^(−2t) +e^(−3t) )) =_(e^t =u) 2(√2)∫_((1+(√3))/( (√2))) ^(+∞) (1/(u^3 +3u +3u^(−1) +u^(−3) )) (du/u) =2(√2) ∫_((1+(√3))/( (√2))) ^(+∞) (du/(u^4 +3u^2 +3 +u^(−2) )) =2(√2) ∫_((1+(√3))/( (√2))) ^(+∞) (u^2 /(u^6 +3u^4 +3u^2 +1))du let decompose F(u) =(u^2 /(u^6 +3u^4 +3 u^2 +1)) we have F(u)=(u^2 /((u^2 +1)^3 )) F(u) =((au +b)/(u^2 +1)) +((cu +d)/((u^2 +1)^2 )) +((eu +f)/((u^2 +1)^3 )) F(−u)=F(u) ⇒a =c=e =0 ⇒F(u) =(b/(u^2 +1)) +(d/((u^2 +1)^2 )) +(f/((u^2 +1)^3 )) lim_(u→+∞) u^2 F(u)=0 =b ⇒F(u) =(d/((u^2 +1)^2 )) +(f/((u^2 +1)^3 )) lim_(u→+∞) u^4 F(u) =1 = d ⇒F(u) =(1/((u^2 +1)^2 )) +(f/((u^2 +1)^3 )) F(0) =0 =1+f ⇒f=−1 ⇒F(u) =(1/((u^2 +1)^2 )) −(1/((u^2 +1)^3 )) ⇒ ∫ F(u)du = ∫ (du/((u^2 +1)^2 )) −∫ (du/((u^2 +1)^3 )) changement u=tanθ give ∫ (du/((1+u^2 )^2 )) =∫ ((1+tan^2 θ)/((1+tan^2 θ)^2 )) dθ = ∫cos^2 θ dθ =∫ ((1+cos(2θ))/2)dθ =(θ/2) +(1/4) sin(2θ) =(θ/2) +(1/4) ((2tanθ)/(1+tan^2 θ)) =((arctan(u))/2) +(u/(1+u^2 )) =((arctan(e^t ))/2) + (e^t /(1+e^(2t) )) =....be continued...
$${let}\:{A}\:=\:\int_{\mathrm{1}} ^{+\infty} \:\frac{{dx}}{{x}^{\mathrm{3}} \sqrt{\mathrm{2}+{x}^{\mathrm{2}} }}{dx}\:{changement}\:{x}\:=\sqrt{\mathrm{2}}{sh}\left({t}\right)\:{give} \\ $$$${A}\:=\:\int_{{argsh}\left(\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\right)} ^{+\infty} \:\:\:\:\:\:\frac{\sqrt{\mathrm{2}}{ch}\left({t}\right){dt}}{\mathrm{2}\sqrt{\mathrm{2}}{sh}^{\mathrm{3}} \left({t}\right)\sqrt{\mathrm{2}}{ch}\left({t}\right)}\:=\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{2}}}\:\int_{{ln}\left(\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}\:}+\sqrt{\frac{\mathrm{3}}{\mathrm{2}}}\right)} ^{+\infty} \:\:\frac{{dt}}{\left(\frac{{e}^{{t}} \:−{e}^{−{t}} }{\mathrm{2}}\right)^{\mathrm{3}} } \\ $$$$=\frac{\mathrm{4}}{\:\sqrt{\mathrm{2}}}\:\:\int_{{ln}\left(\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}+\frac{\sqrt{\mathrm{3}}}{\:\sqrt{\mathrm{2}}}\right)} ^{+\infty} \:\:\:\:\:\:\:\:\:\frac{{dt}}{{e}^{\mathrm{3}{t}} \:+\mathrm{3}\:{e}^{\mathrm{2}{t}} \:{e}^{−{t}} \:+\mathrm{3}\:{e}^{{t}} \:{e}^{−\mathrm{2}{t}} \:+{e}^{−\mathrm{3}{t}} } \\ $$$$=_{{e}^{{t}} ={u}} \:\:\:\:\mathrm{2}\sqrt{\mathrm{2}}\int_{\frac{\mathrm{1}+\sqrt{\mathrm{3}}}{\:\sqrt{\mathrm{2}}}} ^{+\infty} \:\:\:\:\:\:\:\:\:\frac{\mathrm{1}}{{u}^{\mathrm{3}} \:+\mathrm{3}{u}\:\:+\mathrm{3}{u}^{−\mathrm{1}} \:+{u}^{−\mathrm{3}} }\:\frac{{du}}{{u}} \\ $$$$=\mathrm{2}\sqrt{\mathrm{2}}\:\int_{\frac{\mathrm{1}+\sqrt{\mathrm{3}}}{\:\sqrt{\mathrm{2}}}} ^{+\infty} \:\:\:\:\:\:\:\frac{{du}}{{u}^{\mathrm{4}} \:+\mathrm{3}{u}^{\mathrm{2}} \:+\mathrm{3}\:+{u}^{−\mathrm{2}} }\:=\mathrm{2}\sqrt{\mathrm{2}}\:\int_{\frac{\mathrm{1}+\sqrt{\mathrm{3}}}{\:\sqrt{\mathrm{2}}}} ^{+\infty} \:\:\:\:\:\frac{{u}^{\mathrm{2}} }{{u}^{\mathrm{6}} \:+\mathrm{3}{u}^{\mathrm{4}} \:+\mathrm{3}{u}^{\mathrm{2}} \:+\mathrm{1}}{du} \\ $$$${let}\:{decompose}\:{F}\left({u}\right)\:=\frac{{u}^{\mathrm{2}} }{{u}^{\mathrm{6}} \:+\mathrm{3}{u}^{\mathrm{4}} \:+\mathrm{3}\:{u}^{\mathrm{2}} \:+\mathrm{1}}\:\:{we}\:{have}\:{F}\left({u}\right)=\frac{{u}^{\mathrm{2}} }{\left({u}^{\mathrm{2}} \:+\mathrm{1}\right)^{\mathrm{3}} } \\ $$$${F}\left({u}\right)\:=\frac{{au}\:+{b}}{{u}^{\mathrm{2}} \:+\mathrm{1}}\:+\frac{{cu}\:+{d}}{\left({u}^{\mathrm{2}} \:+\mathrm{1}\right)^{\mathrm{2}} }\:+\frac{{eu}\:+{f}}{\left({u}^{\mathrm{2}} \:+\mathrm{1}\right)^{\mathrm{3}} } \\ $$$${F}\left(−{u}\right)={F}\left({u}\right)\:\Rightarrow{a}\:={c}={e}\:=\mathrm{0}\:\Rightarrow{F}\left({u}\right)\:=\frac{{b}}{{u}^{\mathrm{2}} \:+\mathrm{1}}\:+\frac{{d}}{\left({u}^{\mathrm{2}} \:+\mathrm{1}\right)^{\mathrm{2}} }\:+\frac{{f}}{\left({u}^{\mathrm{2}} \:+\mathrm{1}\right)^{\mathrm{3}} } \\ $$$${lim}_{{u}\rightarrow+\infty} {u}^{\mathrm{2}} {F}\left({u}\right)=\mathrm{0}\:={b}\:\Rightarrow{F}\left({u}\right)\:=\frac{{d}}{\left({u}^{\mathrm{2}} \:+\mathrm{1}\right)^{\mathrm{2}} }\:+\frac{{f}}{\left({u}^{\mathrm{2}} \:+\mathrm{1}\right)^{\mathrm{3}} } \\ $$$${lim}_{{u}\rightarrow+\infty} {u}^{\mathrm{4}} \:{F}\left({u}\right)\:=\mathrm{1}\:=\:{d}\:\Rightarrow{F}\left({u}\right)\:=\frac{\mathrm{1}}{\left({u}^{\mathrm{2}} \:+\mathrm{1}\right)^{\mathrm{2}} }\:+\frac{{f}}{\left({u}^{\mathrm{2}} \:+\mathrm{1}\right)^{\mathrm{3}} } \\ $$$${F}\left(\mathrm{0}\right)\:=\mathrm{0}\:=\mathrm{1}+{f}\:\Rightarrow{f}=−\mathrm{1}\:\Rightarrow{F}\left({u}\right)\:=\frac{\mathrm{1}}{\left({u}^{\mathrm{2}} \:+\mathrm{1}\right)^{\mathrm{2}} }\:−\frac{\mathrm{1}}{\left({u}^{\mathrm{2}} \:+\mathrm{1}\right)^{\mathrm{3}} }\:\Rightarrow \\ $$$$\int\:{F}\left({u}\right){du}\:=\:\int\:\:\:\:\frac{{du}}{\left({u}^{\mathrm{2}} \:+\mathrm{1}\right)^{\mathrm{2}} }\:−\int\:\:\:\:\:\frac{{du}}{\left({u}^{\mathrm{2}} \:+\mathrm{1}\right)^{\mathrm{3}} }\:\:{changement}\:{u}={tan}\theta\:{give} \\ $$$$\int\:\:\:\:\:\frac{{du}}{\left(\mathrm{1}+{u}^{\mathrm{2}} \right)^{\mathrm{2}} }\:=\int\:\:\:\frac{\mathrm{1}+{tan}^{\mathrm{2}} \theta}{\left(\mathrm{1}+{tan}^{\mathrm{2}} \theta\right)^{\mathrm{2}} }\:{d}\theta\:=\:\int{cos}^{\mathrm{2}} \theta\:{d}\theta\:\:=\int\:\frac{\mathrm{1}+{cos}\left(\mathrm{2}\theta\right)}{\mathrm{2}}{d}\theta \\ $$$$=\frac{\theta}{\mathrm{2}}\:+\frac{\mathrm{1}}{\mathrm{4}}\:{sin}\left(\mathrm{2}\theta\right)\:=\frac{\theta}{\mathrm{2}}\:+\frac{\mathrm{1}}{\mathrm{4}}\:\frac{\mathrm{2}{tan}\theta}{\mathrm{1}+{tan}^{\mathrm{2}} \theta}\:=\frac{{arctan}\left({u}\right)}{\mathrm{2}}\:+\frac{{u}}{\mathrm{1}+{u}^{\mathrm{2}} } \\ $$$$=\frac{{arctan}\left({e}^{{t}} \right)}{\mathrm{2}}\:+\:\frac{{e}^{{t}} }{\mathrm{1}+{e}^{\mathrm{2}{t}} }\:\:=….{be}\:{continued}… \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 18/Sep/18
x=(√2) tanα dx=(√2) sec^2 α dα ∫_(tan^(−1) ((1/( (√2) )))) ^(Π/2) (((√2) sec^2 αdα)/(2^(3/2) tan^3 α ×(√(2+2tan^2 α)) )) ∫_(tan^(−1) ((1/( (√2))))) ^(Π/2) (((√2) sec^2 α)/(2^2 ×tan^3 α×secα))dα (1/(2(√2) ))∫_(tan^(−1) ((1/( (√2))))) ^(Π/2) ((secα)/(tan^3 α))dα (1/(2(√2) ))∫_(tan^(−1) ((1/( (√2_ ))))) ^(Π/2) ((cos^2 α)/(sin^3 α))dα or approach ∫_1 ^∞ (dx/(x^3 (√(2+x^2 )))) ∫_1 ^∞ ((xdx)/(x^4 (√(2+x^2 )) )) t^2 =2+x^2 2tdt=2xdx ∫ ((tdt)/((t^2 −2)^2 ×t)) ∫ (dt/((t+(√2) )^2 ×(t−(√2) )^2 )) (1/((t^2 −2)^2 ))=(a/(t+(√2)))+(b/((t+(√2))^2 ))+(c/(t−(√2)))+(d/((t−(√2) )^2 )) 1=a(t+(√2) )(t−(√2) )^2 +b(t−(√2) )^2 +c(t−(√2) )(t+(√2) )^2 +d(t+(√2) )^2 t+(√2) =0 1=b(−2(√2) )^2 b=(1/8) t−(√2) =0 1=d(2(√2) )^2 d=(1/8) t=0 1=a×2(√2) +(1/8)×2+c(−2(√2) )+(1/8)×2 1−(1/2)=2(√2) (a−c) a−c=(1/(4(√2) )) t=2(√2) 1=a(3(√2) )(2)+(1/8)(2)+c((√2) )(18)+(1/8)×18 1−(1/4)−(9/4)=6(√2) a+18(√2) c ((4−1−9)/4)=6(√2) (a+3c) a+3c=((−6)/(4×6(√2) ))=((−1)/(4(√2) )) a−c=(1/(4(√2) )) a+3c=((−1)/(4(√2))) −4c=(2/(4(√2) )) c=((−1)/(8(√2) )) a=(1/(4(√2)))−(1/(8(√2) ))=(1/(8(√2) )) ∫(a/(t+(√2) ))dt+∫(b/((t+(√2) )^2 ))dt+∫(c/(t−(√2) ))dt+∫(d/((t−(√2) )^2 )) (1/(8(√2) ))ln(t+(√2) )+(1/8)×((−1)/((t+(√2) )))+((−1)/(8(√2) ))ln(t−(√2) )+(1/8)×((−1)/((t−(√2) ))) (1/(8(√2)))ln(((t+(√2))/(t−(√2) )))−(1/8)((1/(t+(√2) ))+(1/(t−(√2)))) (1/(8(√2) ))ln((((√(2+x^2 )) +(√2))/( (√(2+x^2 )) −(√2))))−(1/8)(((2(√(2+x^2 )) )/(2+x^2 −2))) ans is ∣(1/(8(√2)))ln((((√(2+x^2 )) +(√2))/( (√(2+x^2 )) −(√2))))−(1/4)(((√(2+x^2 ))/x^2 ))∣_1 ^∞ =(1/(8(√2)))∣ln(((1+(((√2) )/( (√(2+x^2 )) )))/(1−((√2)/( (√(2+x^2 )))))))−(1/4)((x/x^2 )(√(1+(2/x^2 ))) )∣_1 ^∞ =(1/(8(√2)))[{ln(((1+0)/(1−0)))−(1/4)(0×(√(1+0)) }−{ln((((√3) +(√2))/( (√3) −(√2))))−(1/4)((√3) ) (1/(8(√2)))[((√3)/4)−ln((((√3) +(√2))/( (√3) −(√2))))]
$${x}=\sqrt{\mathrm{2}}\:{tan}\alpha\:\:{dx}=\sqrt{\mathrm{2}}\:{sec}^{\mathrm{2}} \alpha\:{d}\alpha \\ $$$$\int_{{tan}^{−\mathrm{1}} \left(\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}\:}\right)} ^{\frac{\Pi}{\mathrm{2}}} \:\frac{\sqrt{\mathrm{2}}\:{sec}^{\mathrm{2}} \alpha{d}\alpha}{\mathrm{2}^{\frac{\mathrm{3}}{\mathrm{2}}} {tan}^{\mathrm{3}} \alpha\:×\sqrt{\mathrm{2}+\mathrm{2}{tan}^{\mathrm{2}} \alpha}\:} \\ $$$$\int_{{tan}^{−\mathrm{1}} \left(\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\right)} ^{\frac{\Pi}{\mathrm{2}}} \:\:\frac{\sqrt{\mathrm{2}}\:{sec}^{\mathrm{2}} \alpha}{\mathrm{2}^{\mathrm{2}} ×{tan}^{\mathrm{3}} \alpha×{sec}\alpha}{d}\alpha \\ $$$$\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{2}}\:}\int_{{tan}^{−\mathrm{1}} \left(\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\right)} ^{\frac{\Pi}{\mathrm{2}}} \:\:\frac{{sec}\alpha}{{tan}^{\mathrm{3}} \alpha}{d}\alpha \\ $$$$\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{2}}\:}\int_{{tan}^{−\mathrm{1}} \left(\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}_{} }}\right)} ^{\frac{\Pi}{\mathrm{2}}} \:\frac{{cos}^{\mathrm{2}} \alpha}{{sin}^{\mathrm{3}} \alpha}{d}\alpha \\ $$$$ \\ $$$$ \\ $$$${or}\:{approach} \\ $$$$\int_{\mathrm{1}} ^{\infty} \frac{{dx}}{{x}^{\mathrm{3}} \sqrt{\mathrm{2}+{x}^{\mathrm{2}} }} \\ $$$$\int_{\mathrm{1}} ^{\infty} \frac{{xdx}}{{x}^{\mathrm{4}} \sqrt{\mathrm{2}+{x}^{\mathrm{2}} }\:} \\ $$$$ \\ $$$${t}^{\mathrm{2}} =\mathrm{2}+{x}^{\mathrm{2}} \:\:\:\:\mathrm{2}{tdt}=\mathrm{2}{xdx} \\ $$$$\int\:\frac{{tdt}}{\left({t}^{\mathrm{2}} −\mathrm{2}\right)^{\mathrm{2}} ×{t}} \\ $$$$\int\:\frac{{dt}}{\left({t}+\sqrt{\mathrm{2}}\:\right)^{\mathrm{2}} ×\left({t}−\sqrt{\mathrm{2}}\:\right)^{\mathrm{2}} } \\ $$$$\frac{\mathrm{1}}{\left({t}^{\mathrm{2}} −\mathrm{2}\right)^{\mathrm{2}} }=\frac{{a}}{{t}+\sqrt{\mathrm{2}}}+\frac{{b}}{\left({t}+\sqrt{\mathrm{2}}\right)^{\mathrm{2}} }+\frac{{c}}{{t}−\sqrt{\mathrm{2}}}+\frac{{d}}{\left({t}−\sqrt{\mathrm{2}}\:\right)^{\mathrm{2}} } \\ $$$$\mathrm{1}={a}\left({t}+\sqrt{\mathrm{2}}\:\right)\left({t}−\sqrt{\mathrm{2}}\:\right)^{\mathrm{2}} +{b}\left({t}−\sqrt{\mathrm{2}}\:\right)^{\mathrm{2}} +{c}\left({t}−\sqrt{\mathrm{2}}\:\right)\left({t}+\sqrt{\mathrm{2}}\:\right)^{\mathrm{2}} +{d}\left({t}+\sqrt{\mathrm{2}}\:\right)^{\mathrm{2}} \\ $$$${t}+\sqrt{\mathrm{2}}\:=\mathrm{0}\:\:\mathrm{1}={b}\left(−\mathrm{2}\sqrt{\mathrm{2}}\:\right)^{\mathrm{2}} \:\:{b}=\frac{\mathrm{1}}{\mathrm{8}} \\ $$$${t}−\sqrt{\mathrm{2}}\:=\mathrm{0}\:\:\:\mathrm{1}={d}\left(\mathrm{2}\sqrt{\mathrm{2}}\:\right)^{\mathrm{2}} \:\:{d}=\frac{\mathrm{1}}{\mathrm{8}} \\ $$$${t}=\mathrm{0}\:\:\mathrm{1}={a}×\mathrm{2}\sqrt{\mathrm{2}}\:+\frac{\mathrm{1}}{\mathrm{8}}×\mathrm{2}+{c}\left(−\mathrm{2}\sqrt{\mathrm{2}}\:\right)+\frac{\mathrm{1}}{\mathrm{8}}×\mathrm{2} \\ $$$$\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}}=\mathrm{2}\sqrt{\mathrm{2}}\:\:\left({a}−{c}\right) \\ $$$${a}−{c}=\frac{\mathrm{1}}{\mathrm{4}\sqrt{\mathrm{2}}\:} \\ $$$${t}=\mathrm{2}\sqrt{\mathrm{2}}\: \\ $$$$\mathrm{1}={a}\left(\mathrm{3}\sqrt{\mathrm{2}}\:\right)\left(\mathrm{2}\right)+\frac{\mathrm{1}}{\mathrm{8}}\left(\mathrm{2}\right)+{c}\left(\sqrt{\mathrm{2}}\:\right)\left(\mathrm{18}\right)+\frac{\mathrm{1}}{\mathrm{8}}×\mathrm{18} \\ $$$$\mathrm{1}−\frac{\mathrm{1}}{\mathrm{4}}−\frac{\mathrm{9}}{\mathrm{4}}=\mathrm{6}\sqrt{\mathrm{2}}\:{a}+\mathrm{18}\sqrt{\mathrm{2}}\:{c} \\ $$$$\frac{\mathrm{4}−\mathrm{1}−\mathrm{9}}{\mathrm{4}}=\mathrm{6}\sqrt{\mathrm{2}}\:\left({a}+\mathrm{3}{c}\right) \\ $$$${a}+\mathrm{3}{c}=\frac{−\mathrm{6}}{\mathrm{4}×\mathrm{6}\sqrt{\mathrm{2}}\:}=\frac{−\mathrm{1}}{\mathrm{4}\sqrt{\mathrm{2}}\:} \\ $$$${a}−{c}=\frac{\mathrm{1}}{\mathrm{4}\sqrt{\mathrm{2}}\:} \\ $$$${a}+\mathrm{3}{c}=\frac{−\mathrm{1}}{\mathrm{4}\sqrt{\mathrm{2}}} \\ $$$$−\mathrm{4}{c}=\frac{\mathrm{2}}{\mathrm{4}\sqrt{\mathrm{2}}\:} \\ $$$${c}=\frac{−\mathrm{1}}{\mathrm{8}\sqrt{\mathrm{2}}\:} \\ $$$${a}=\frac{\mathrm{1}}{\mathrm{4}\sqrt{\mathrm{2}}}−\frac{\mathrm{1}}{\mathrm{8}\sqrt{\mathrm{2}}\:}=\frac{\mathrm{1}}{\mathrm{8}\sqrt{\mathrm{2}}\:} \\ $$$$\int\frac{{a}}{{t}+\sqrt{\mathrm{2}}\:}{dt}+\int\frac{{b}}{\left({t}+\sqrt{\mathrm{2}}\:\right)^{\mathrm{2}} }{dt}+\int\frac{{c}}{{t}−\sqrt{\mathrm{2}}\:}{dt}+\int\frac{{d}}{\left({t}−\sqrt{\mathrm{2}}\:\right)^{\mathrm{2}} } \\ $$$$\frac{\mathrm{1}}{\mathrm{8}\sqrt{\mathrm{2}}\:}{ln}\left({t}+\sqrt{\mathrm{2}}\:\right)+\frac{\mathrm{1}}{\mathrm{8}}×\frac{−\mathrm{1}}{\left({t}+\sqrt{\mathrm{2}}\:\right)}+\frac{−\mathrm{1}}{\mathrm{8}\sqrt{\mathrm{2}}\:}{ln}\left({t}−\sqrt{\mathrm{2}}\:\:\right)+\frac{\mathrm{1}}{\mathrm{8}}×\frac{−\mathrm{1}}{\left({t}−\sqrt{\mathrm{2}}\:\right)} \\ $$$$\frac{\mathrm{1}}{\mathrm{8}\sqrt{\mathrm{2}}}{ln}\left(\frac{{t}+\sqrt{\mathrm{2}}}{{t}−\sqrt{\mathrm{2}}\:}\right)−\frac{\mathrm{1}}{\mathrm{8}}\left(\frac{\mathrm{1}}{{t}+\sqrt{\mathrm{2}}\:}+\frac{\mathrm{1}}{{t}−\sqrt{\mathrm{2}}}\right) \\ $$$$\frac{\mathrm{1}}{\mathrm{8}\sqrt{\mathrm{2}}\:}{ln}\left(\frac{\sqrt{\mathrm{2}+{x}^{\mathrm{2}} }\:+\sqrt{\mathrm{2}}}{\:\sqrt{\mathrm{2}+{x}^{\mathrm{2}} }\:\:−\sqrt{\mathrm{2}}}\right)−\frac{\mathrm{1}}{\mathrm{8}}\left(\frac{\mathrm{2}\sqrt{\mathrm{2}+{x}^{\mathrm{2}} }\:}{\mathrm{2}+{x}^{\mathrm{2}} −\mathrm{2}}\right) \\ $$$${ans}\:{is} \\ $$$$\mid\frac{\mathrm{1}}{\mathrm{8}\sqrt{\mathrm{2}}}{ln}\left(\frac{\sqrt{\mathrm{2}+{x}^{\mathrm{2}} }\:+\sqrt{\mathrm{2}}}{\:\sqrt{\mathrm{2}+{x}^{\mathrm{2}} }\:−\sqrt{\mathrm{2}}}\right)−\frac{\mathrm{1}}{\mathrm{4}}\left(\frac{\sqrt{\mathrm{2}+{x}^{\mathrm{2}} }}{{x}^{\mathrm{2}} }\right)\mid_{\mathrm{1}} ^{\infty} \\ $$$$=\frac{\mathrm{1}}{\mathrm{8}\sqrt{\mathrm{2}}}\mid{ln}\left(\frac{\mathrm{1}+\frac{\sqrt{\mathrm{2}}\:}{\:\sqrt{\mathrm{2}+{x}^{\mathrm{2}} }\:}}{\mathrm{1}−\frac{\sqrt{\mathrm{2}}}{\:\sqrt{\mathrm{2}+{x}^{\mathrm{2}} \:}}}\right)−\frac{\mathrm{1}}{\mathrm{4}}\left(\frac{{x}}{{x}^{\mathrm{2}} }\sqrt{\mathrm{1}+\frac{\mathrm{2}}{{x}^{\mathrm{2}} }}\:\right)\mid_{\mathrm{1}} ^{\infty} \\ $$$$=\frac{\mathrm{1}}{\mathrm{8}\sqrt{\mathrm{2}}}\left[\left\{{ln}\left(\frac{\mathrm{1}+\mathrm{0}}{\mathrm{1}−\mathrm{0}}\right)−\frac{\mathrm{1}}{\mathrm{4}}\left(\mathrm{0}×\sqrt{\mathrm{1}+\mathrm{0}}\:\right\}−\left\{{ln}\left(\frac{\sqrt{\mathrm{3}}\:+\sqrt{\mathrm{2}}}{\:\sqrt{\mathrm{3}}\:−\sqrt{\mathrm{2}}}\right)−\frac{\mathrm{1}}{\mathrm{4}}\left(\sqrt{\mathrm{3}}\:\right)\right.\right.\right. \\ $$$$\frac{\mathrm{1}}{\mathrm{8}\sqrt{\mathrm{2}}}\left[\frac{\sqrt{\mathrm{3}}}{\mathrm{4}}−{ln}\left(\frac{\sqrt{\mathrm{3}}\:+\sqrt{\mathrm{2}}}{\:\sqrt{\mathrm{3}}\:−\sqrt{\mathrm{2}}}\right)\right] \\ $$$$ \\ $$$$ \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *