Question Number 38119 by maxmathsup by imad last updated on 22/Jun/18
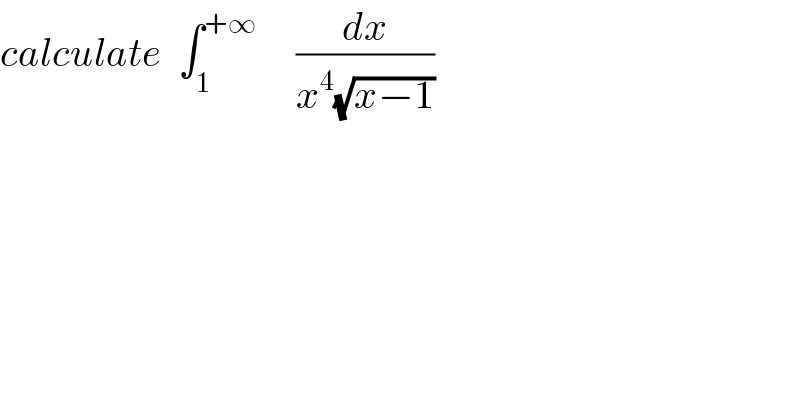
$${calculate}\:\:\int_{\mathrm{1}} ^{+\infty} \:\:\:\:\:\frac{{dx}}{{x}^{\mathrm{4}} \sqrt{{x}−\mathrm{1}}} \\ $$
Commented by math khazana by abdo last updated on 22/Jun/18
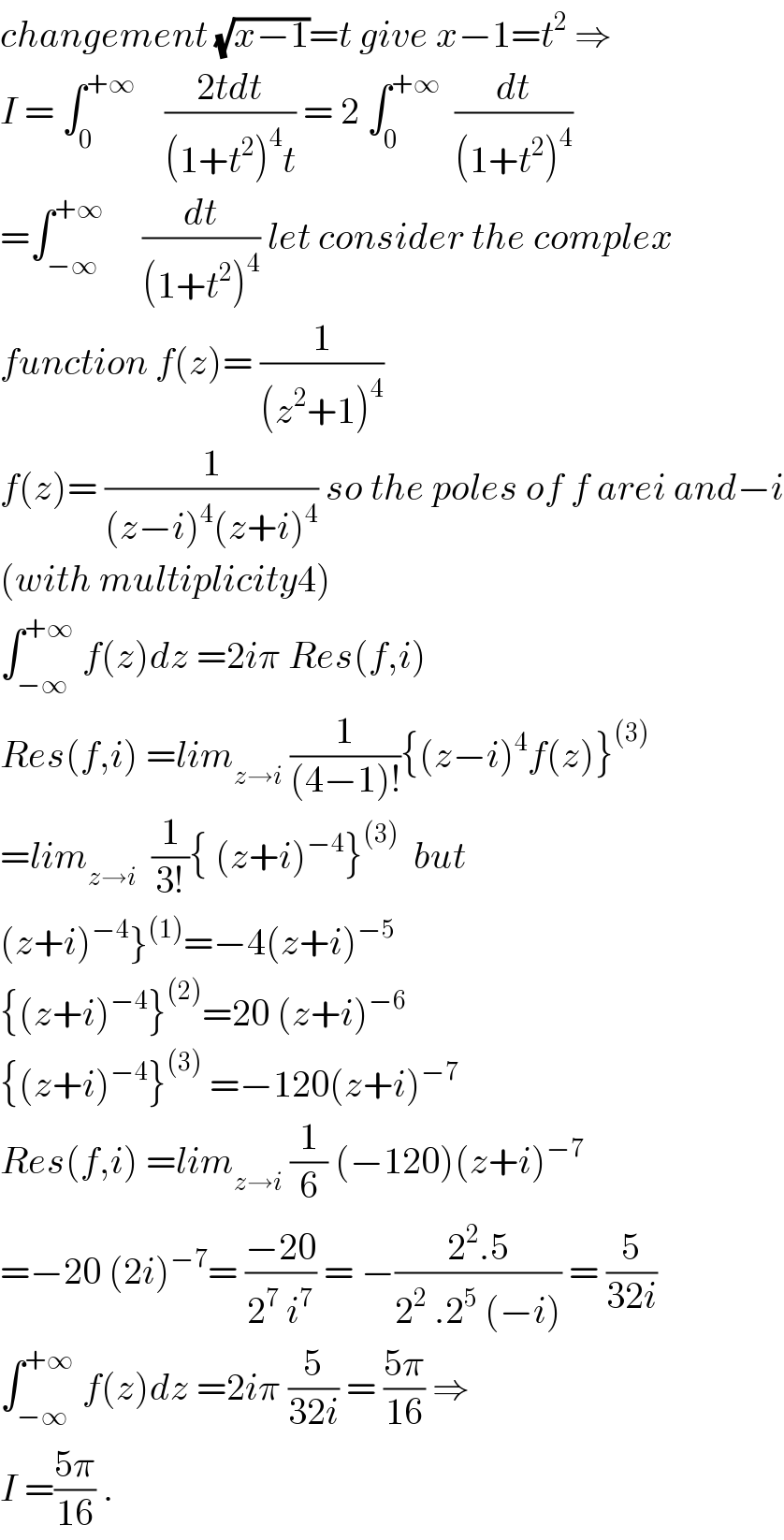
$${changement}\:\sqrt{{x}−\mathrm{1}}={t}\:{give}\:{x}−\mathrm{1}={t}^{\mathrm{2}} \:\Rightarrow \\ $$$${I}\:=\:\int_{\mathrm{0}} ^{+\infty} \:\:\:\:\frac{\mathrm{2}{tdt}}{\left(\mathrm{1}+{t}^{\mathrm{2}} \right)^{\mathrm{4}} {t}}\:=\:\mathrm{2}\:\int_{\mathrm{0}} ^{+\infty} \:\:\frac{{dt}}{\left(\mathrm{1}+{t}^{\mathrm{2}} \right)^{\mathrm{4}} } \\ $$$$=\int_{−\infty} ^{+\infty} \:\:\:\:\:\frac{{dt}}{\left(\mathrm{1}+{t}^{\mathrm{2}} \right)^{\mathrm{4}} }\:{let}\:{consider}\:{the}\:{complex}\: \\ $$$${function}\:{f}\left({z}\right)=\:\frac{\mathrm{1}}{\left({z}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{4}} } \\ $$$${f}\left({z}\right)=\:\frac{\mathrm{1}}{\left({z}−{i}\right)^{\mathrm{4}} \left({z}+{i}\right)^{\mathrm{4}} }\:{so}\:{the}\:{poles}\:{of}\:{f}\:{arei}\:{and}−{i} \\ $$$$\left({with}\:{multiplicity}\mathrm{4}\right) \\ $$$$\int_{−\infty} ^{+\infty} \:{f}\left({z}\right){dz}\:=\mathrm{2}{i}\pi\:{Res}\left({f},{i}\right) \\ $$$${Res}\left({f},{i}\right)\:={lim}_{{z}\rightarrow{i}} \:\frac{\mathrm{1}}{\left(\mathrm{4}−\mathrm{1}\right)!}\left\{\left({z}−{i}\right)^{\mathrm{4}} {f}\left({z}\right)\right\}^{\left(\mathrm{3}\right)} \\ $$$$={lim}_{{z}\rightarrow{i}} \:\:\frac{\mathrm{1}}{\mathrm{3}!}\left\{\:\left({z}+{i}\right)^{−\mathrm{4}} \right\}^{\left(\mathrm{3}\right)} \:\:{but} \\ $$$$\left.\left({z}+{i}\right)^{−\mathrm{4}} \right\}^{\left(\mathrm{1}\right)} =−\mathrm{4}\left({z}+{i}\right)^{−\mathrm{5}} \\ $$$$\left\{\left({z}+{i}\right)^{−\mathrm{4}} \right\}^{\left(\mathrm{2}\right)} =\mathrm{20}\:\left({z}+{i}\right)^{−\mathrm{6}} \\ $$$$\left\{\left({z}+{i}\right)^{−\mathrm{4}} \right\}^{\left(\mathrm{3}\right)} \:=−\mathrm{120}\left({z}+{i}\right)^{−\mathrm{7}} \\ $$$${Res}\left({f},{i}\right)\:={lim}_{{z}\rightarrow{i}} \:\frac{\mathrm{1}}{\mathrm{6}}\:\left(−\mathrm{120}\right)\left({z}+{i}\right)^{−\mathrm{7}} \\ $$$$=−\mathrm{20}\:\left(\mathrm{2}{i}\right)^{−\mathrm{7}} =\:\frac{−\mathrm{20}}{\mathrm{2}^{\mathrm{7}} \:{i}^{\mathrm{7}} }\:=\:−\frac{\mathrm{2}^{\mathrm{2}} .\mathrm{5}}{\mathrm{2}^{\mathrm{2}} \:.\mathrm{2}^{\mathrm{5}} \:\left(−{i}\right)}\:=\:\frac{\mathrm{5}}{\mathrm{32}{i}} \\ $$$$\int_{−\infty} ^{+\infty} \:{f}\left({z}\right){dz}\:=\mathrm{2}{i}\pi\:\frac{\mathrm{5}}{\mathrm{32}{i}}\:=\:\frac{\mathrm{5}\pi}{\mathrm{16}}\:\Rightarrow \\ $$$${I}\:=\frac{\mathrm{5}\pi}{\mathrm{16}}\:. \\ $$
