Question Number 64390 by mathmax by abdo last updated on 17/Jul/19
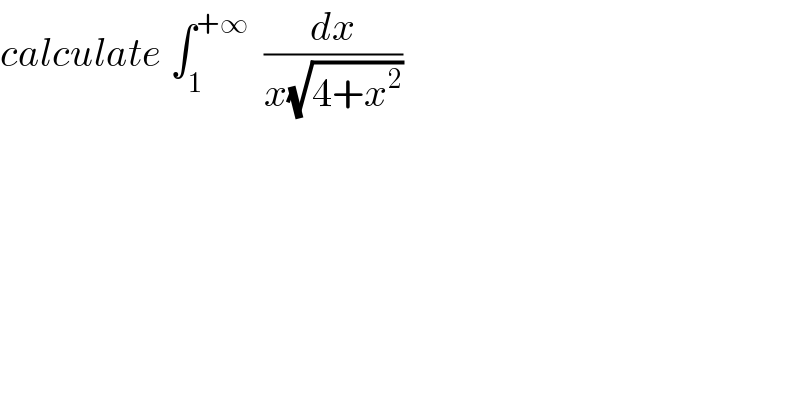
$${calculate}\:\int_{\mathrm{1}} ^{+\infty} \:\:\frac{{dx}}{{x}\sqrt{\mathrm{4}+{x}^{\mathrm{2}} }} \\ $$
Commented by mathmax by abdo last updated on 18/Jul/19
![let I =∫_1 ^(+∞) (dx/(x(√(4+x^2 )))) changement x= 2tanθ give I =∫_(arctan((1/2))) ^(π/2) ((2(1+tan^2 θ)dθ)/(2tanθ×2(√(1+tan^2 θ)))) =(1/2) ∫_(arctan((1/2))) ^(π/2) ((√(1+tan^2 θ))/(tanθ))dθ =(1/2) ∫_(arctan((1/2))) ^(π/2) (1/(cosθ ((sinθ)/(cosθ))))dθ =(1/2) ∫_(arctan((1/2))) ^(π/2) (dθ/(sinθ)) =_(tan((θ/2))=u) (1/2) ∫_(tan((1/2)arctan((1/2)))) ^1 ((2du)/((1+u^2 )((2u)/(1+u^2 )))) = ∫_λ ^1 (du/(2u)) =(1/2)ln∣u∣]_λ ^1 =−(1/2)lnλ =−(1/2)ln(tan((1/2)arctan((1/2)))](https://www.tinkutara.com/question/Q64441.png)
$${let}\:{I}\:=\int_{\mathrm{1}} ^{+\infty} \:\:\frac{{dx}}{{x}\sqrt{\mathrm{4}+{x}^{\mathrm{2}} }}\:\:{changement}\:\:{x}=\:\mathrm{2}{tan}\theta\:\:{give} \\ $$$${I}\:=\int_{{arctan}\left(\frac{\mathrm{1}}{\mathrm{2}}\right)} ^{\frac{\pi}{\mathrm{2}}} \:\:\frac{\mathrm{2}\left(\mathrm{1}+{tan}^{\mathrm{2}} \theta\right){d}\theta}{\mathrm{2}{tan}\theta×\mathrm{2}\sqrt{\mathrm{1}+{tan}^{\mathrm{2}} \theta}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\:\int_{{arctan}\left(\frac{\mathrm{1}}{\mathrm{2}}\right)} ^{\frac{\pi}{\mathrm{2}}} \:\:\frac{\sqrt{\mathrm{1}+{tan}^{\mathrm{2}} \theta}}{{tan}\theta}{d}\theta\:=\frac{\mathrm{1}}{\mathrm{2}}\:\int_{{arctan}\left(\frac{\mathrm{1}}{\mathrm{2}}\right)} ^{\frac{\pi}{\mathrm{2}}} \:\frac{\mathrm{1}}{{cos}\theta\:\frac{{sin}\theta}{{cos}\theta}}{d}\theta \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\:\int_{{arctan}\left(\frac{\mathrm{1}}{\mathrm{2}}\right)} ^{\frac{\pi}{\mathrm{2}}} \:\frac{{d}\theta}{{sin}\theta}\:=_{{tan}\left(\frac{\theta}{\mathrm{2}}\right)={u}} \:\:\:\frac{\mathrm{1}}{\mathrm{2}}\:\int_{{tan}\left(\frac{\mathrm{1}}{\mathrm{2}}{arctan}\left(\frac{\mathrm{1}}{\mathrm{2}}\right)\right)} ^{\mathrm{1}} \:\:\frac{\mathrm{2}{du}}{\left(\mathrm{1}+{u}^{\mathrm{2}} \right)\frac{\mathrm{2}{u}}{\mathrm{1}+{u}^{\mathrm{2}} }} \\ $$$$\left.=\:\int_{\lambda} ^{\mathrm{1}} \:\:\frac{{du}}{\mathrm{2}{u}}\:=\frac{\mathrm{1}}{\mathrm{2}}{ln}\mid{u}\mid\right]_{\lambda} ^{\mathrm{1}} \:=−\frac{\mathrm{1}}{\mathrm{2}}{ln}\lambda\:=−\frac{\mathrm{1}}{\mathrm{2}}{ln}\left({tan}\left(\frac{\mathrm{1}}{\mathrm{2}}{arctan}\left(\frac{\mathrm{1}}{\mathrm{2}}\right)\right)\right. \\ $$
Commented by mathmax by abdo last updated on 18/Jul/19
![another way we use the changement x =2sh(t) ⇒ A =∫_(argsh((1/2))) ^(+∞) ((2ch(t)dt)/(2sh(t)2 ch(t))) =(1/2) ∫_(ln((1/2)+(√(1+(1/4))))) ^(+∞) (dt/((e^t −e^(−t) )/2)) =∫_(ln((1/2)+((√5)/2))) ^(+∞) (dt/(e^t −e^(−t) )) =_(e^t =u) ∫_((1+(√5))/2) ^(+∞) (du/(u(u−(1/u)))) =∫_((1+(√5))/2) ^(+∞) (du/(u^2 −1)) =(1/2) ∫_((1+(√5))/2) ^(+∞) {(1/(u−1)) −(1/(u+1))}du =(1/2)[ln∣((u−1)/(u+1))∣]_((1+(√5))/2) ^(+∞) =(1/2){ −ln∣((((1+(√5))/2)−1)/(((1+(√5))/2)+1))∣} =−(1/2)ln∣(((√5)−1)/( (√5)+3))∣ =(1/2)ln((((√5)+3)/( (√5)−1))) .](https://www.tinkutara.com/question/Q64442.png)
$${another}\:{way}\:\:{we}\:{use}\:{the}\:{changement}\:{x}\:=\mathrm{2}{sh}\left({t}\right)\:\Rightarrow \\ $$$${A}\:=\int_{{argsh}\left(\frac{\mathrm{1}}{\mathrm{2}}\right)} ^{+\infty} \:\:\frac{\mathrm{2}{ch}\left({t}\right){dt}}{\mathrm{2}{sh}\left({t}\right)\mathrm{2}\:{ch}\left({t}\right)}\:=\frac{\mathrm{1}}{\mathrm{2}}\:\int_{{ln}\left(\frac{\mathrm{1}}{\mathrm{2}}+\sqrt{\left.\mathrm{1}+\frac{\mathrm{1}}{\mathrm{4}}\right)}\right.} ^{+\infty} \:\frac{{dt}}{\frac{{e}^{{t}} −{e}^{−{t}} }{\mathrm{2}}} \\ $$$$=\int_{{ln}\left(\frac{\mathrm{1}}{\mathrm{2}}+\frac{\sqrt{\mathrm{5}}}{\mathrm{2}}\right)} ^{+\infty} \:\:\:\frac{{dt}}{{e}^{{t}} −{e}^{−{t}} }\:=_{{e}^{{t}} ={u}} \:\:\:\int_{\frac{\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{2}}} ^{+\infty} \:\:\:\:\frac{{du}}{{u}\left({u}−\frac{\mathrm{1}}{{u}}\right)} \\ $$$$=\int_{\frac{\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{2}}} ^{+\infty} \:\:\:\frac{{du}}{{u}^{\mathrm{2}} −\mathrm{1}}\:=\frac{\mathrm{1}}{\mathrm{2}}\:\int_{\frac{\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{2}}} ^{+\infty} \left\{\frac{\mathrm{1}}{{u}−\mathrm{1}}\:−\frac{\mathrm{1}}{{u}+\mathrm{1}}\right\}{du} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\left[{ln}\mid\frac{{u}−\mathrm{1}}{{u}+\mathrm{1}}\mid\right]_{\frac{\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{2}}} ^{+\infty} \:=\frac{\mathrm{1}}{\mathrm{2}}\left\{\:−{ln}\mid\frac{\frac{\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{2}}−\mathrm{1}}{\frac{\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{2}}+\mathrm{1}}\mid\right\} \\ $$$$=−\frac{\mathrm{1}}{\mathrm{2}}{ln}\mid\frac{\sqrt{\mathrm{5}}−\mathrm{1}}{\:\sqrt{\mathrm{5}}+\mathrm{3}}\mid\:=\frac{\mathrm{1}}{\mathrm{2}}{ln}\left(\frac{\sqrt{\mathrm{5}}+\mathrm{3}}{\:\sqrt{\mathrm{5}}−\mathrm{1}}\right)\:. \\ $$
Answered by Tanmay chaudhury last updated on 17/Jul/19
![∫((xdx)/(x^2 (√(4+x^2 )) )) t^2 =4+x^2 2tdt=2xdx ∫((tdt)/((t^2 −4)t)) (1/4)∫(((t+2)−(t−2))/((t+2)(t−2)))dt (1/4)[∫(dt/(t−2))−∫(dt/(t+2))] (1/4)ln(((t−2)/(t+2)))+c (1/4)ln((((√(4+x^2 )) −2)/( (√(4+x^2 )) +2)))+c (1/4)∣ln((((√(4+x^2 )) −2)/( (√(4+x^2 )) +2)))∣_1 ^(+∞) (1/4)∣ln(((1−(2/( (√(4+x^2 ))[)))/(1+(2/( (√(4+x^2 )) )))))∣_1 ^(+∞) =(1/4)(ln(((1−0)/(1+0)))−ln((((√5) −2)/( (√5) +2)))) =−(1/4)×ln((((√5) −2)/( (√5) +2)))](https://www.tinkutara.com/question/Q64403.png)
$$\int\frac{{xdx}}{{x}^{\mathrm{2}} \sqrt{\mathrm{4}+{x}^{\mathrm{2}} }\:} \\ $$$${t}^{\mathrm{2}} =\mathrm{4}+{x}^{\mathrm{2}} \:\:\:\mathrm{2}{tdt}=\mathrm{2}{xdx} \\ $$$$\int\frac{{tdt}}{\left({t}^{\mathrm{2}} −\mathrm{4}\right){t}} \\ $$$$\frac{\mathrm{1}}{\mathrm{4}}\int\frac{\left({t}+\mathrm{2}\right)−\left({t}−\mathrm{2}\right)}{\left({t}+\mathrm{2}\right)\left({t}−\mathrm{2}\right)}{dt} \\ $$$$\frac{\mathrm{1}}{\mathrm{4}}\left[\int\frac{{dt}}{{t}−\mathrm{2}}−\int\frac{{dt}}{{t}+\mathrm{2}}\right] \\ $$$$\frac{\mathrm{1}}{\mathrm{4}}{ln}\left(\frac{{t}−\mathrm{2}}{{t}+\mathrm{2}}\right)+{c} \\ $$$$\frac{\mathrm{1}}{\mathrm{4}}{ln}\left(\frac{\sqrt{\mathrm{4}+{x}^{\mathrm{2}} }\:−\mathrm{2}}{\:\sqrt{\mathrm{4}+{x}^{\mathrm{2}} }\:+\mathrm{2}}\right)+{c} \\ $$$$\frac{\mathrm{1}}{\mathrm{4}}\mid{ln}\left(\frac{\sqrt{\mathrm{4}+{x}^{\mathrm{2}} }\:−\mathrm{2}}{\:\sqrt{\mathrm{4}+{x}^{\mathrm{2}} }\:+\mathrm{2}}\right)\mid_{\mathrm{1}} ^{+\infty} \\ $$$$\frac{\mathrm{1}}{\mathrm{4}}\mid{ln}\left(\frac{\mathrm{1}−\frac{\mathrm{2}}{\:\sqrt{\mathrm{4}+{x}^{\mathrm{2}} }\left[\right.}}{\mathrm{1}+\frac{\mathrm{2}}{\:\sqrt{\mathrm{4}+{x}^{\mathrm{2}} }\:}}\right)\mid_{\mathrm{1}} ^{+\infty} \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}}\left({ln}\left(\frac{\mathrm{1}−\mathrm{0}}{\mathrm{1}+\mathrm{0}}\right)−{ln}\left(\frac{\sqrt{\mathrm{5}}\:−\mathrm{2}}{\:\sqrt{\mathrm{5}}\:+\mathrm{2}}\right)\right) \\ $$$$=−\frac{\mathrm{1}}{\mathrm{4}}×{ln}\left(\frac{\sqrt{\mathrm{5}}\:−\mathrm{2}}{\:\sqrt{\mathrm{5}}\:+\mathrm{2}}\right) \\ $$
