calculate-1-e-1-ln-x-ln-1-x-dx-

Question Number 89891 by mathmax by abdo last updated on 19/Apr/20

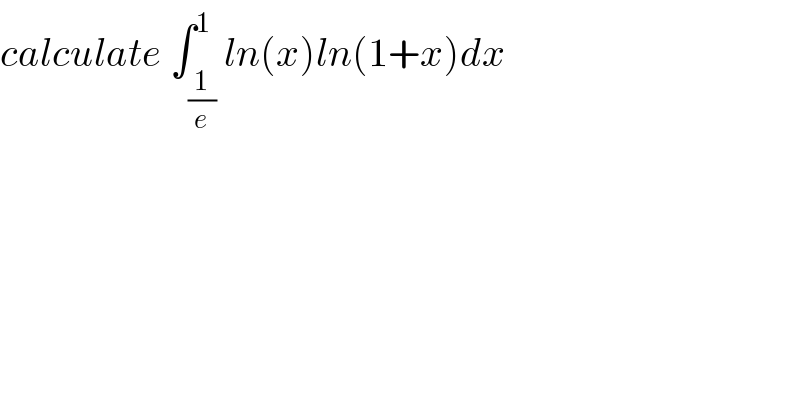
c a l c u l a t e \int_{\frac{1}{e}}^{1} l n (x) l n (1 + x) d x

Commented by mathmax by abdo last updated on 20/Apr/20

l e t t a k e a t r y I = \int_{e^{- 1}}^{e} l n (x) l n (1 + x) d x

w e h a v e {l n}^{^{'}} (1 + x) = \sum_{n = 0}^{\infty} {(- 1)}^{n} x^{n} \Rightarrow l n (1 + x) = \sum_{n = 0}^{\infty} {(- 1)}^{n} \frac{x^{n + 1}}{n + 1}

= \sum_{n = 1}^{\infty} {(- 1)}^{n - 1} \frac{x^{n}}{n} \Rightarrow I = \int_{e^{-}}^{e} l n (x) (\sum_{n = 1}^{\infty} {(- 1)}^{n - 1} \frac{x^{n}}{n}) d x

= \sum_{n = 1}^{\infty} \frac{{(- 1)}^{n - 1}}{n} \int_{e^{- 1}}^{e} x^{n} l n (x) d x

A_{n} = \int_{e^{- 1}}^{e} x^{n} l n (x) d x =_{b y p s r t s} {[\frac{x^{n + 1}}{n + 1} l n (x)]}_{e^{- 1}}^{e} - \int_{e^{- 1}}^{e} \frac{x^{n}}{n + 1} d x

= \frac{1}{(n + 1)} {e^{n + 1} + {(e^{- 1})}^{n + 1}} - \frac{1}{(n + 1)} {[\frac{1}{n + 1} x^{n + 1}]}_{e^{- 1}}^{e}

= \frac{e^{n + 1}}{(n + 1)} + \frac{e^{- n - 1}}{n + 1} - \frac{1}{{(n + 1)}^{2}} (e^{n + 1} - e^{- n - 1}) \Rightarrow

I = \sum_{n = 1}^{\infty} \frac{{(- 1)}^{n - 1} e^{n + 1}}{n (n + 1)} + \sum_{n = 1}^{\infty} \frac{{(- 1)}^{n - 1} e^{- n - 1}}{n (n + 1)}

- \sum_{n = 1}^{\infty} \frac{{(- 1)}^{n - 1}}{n {(n + 1)}^{2}} e^{n + 1} - \sum_{n = 1}^{\infty} \frac{{(- 1)}^{n - 1}}{n {(n + 1)}^{2}} e^{- n - 1} w e h a v e

\sum_{n = 1}^{\infty} \frac{{(- 1)}^{n - 1}}{n (n + 1)} e^{n + 1} = \sum_{n = 1}^{\infty} (\frac{1}{n} - \frac{1}{n + 1}) {(- 1)}^{n - 1} e^{n + 1}

= e \sum_{n = 1}^{\infty} \frac{{(- 1)}^{n - 1}}{n} e^{n} - \sum_{n = 1}^{\infty} \frac{{(- 1)}^{n - 1}}{n + 1} e^{n + 1}

= e l n (1 + e) + \sum_{n = 2}^{\infty} \frac{{(- 1)}^{n - 1}}{n} e^{n}

= e l n (1 + e) + l n (1 + e) = (1 + e) l n (1 + e)

l e t d e c o m p o s e F (x) = \frac{1}{x {(x + 1)}^{2}} = \frac{a}{x} + \frac{b}{x + 1} + \frac{c}{{(x + 1)}^{2}}

c = - 1

{l i m}_{x \to + \infty} x F (x) = 0 = a + b \Rightarrow b = - a \Rightarrow

F (x) = \frac{a}{x} - \frac{a}{x + 1} - \frac{1}{{(x + 1)}^{2}}

F (1) = \frac{1}{4} = a - \frac{a}{2} - \frac{1}{4} = \frac{a}{2} - \frac{1}{4} \Rightarrow \frac{1}{2} = \frac{a}{2} \Rightarrow a = 1 \Rightarrow

F (x) = \frac{1}{x} - \frac{1}{x + 1} - \frac{1}{{(x + 1)}^{2}} \Rightarrow

\sum_{n = 1}^{\infty} \frac{{(- 1)}^{n - 1}}{n {(n + 1)}^{2}} e^{n + 1} = \sum_{n = 1}^{\infty} {(- 1)}^{n - 1} (\frac{1}{n} - \frac{1}{n + 1} - \frac{1}{{(n + 1)}^{2}}) e^{n + 1}

= \sum_{n = 1}^{\infty} \frac{{(- 1)}^{n - 1}}{n} e^{n + 1} - \sum_{n = 1}^{\infty} \frac{{(- 1)}^{n - 1}}{n + 1} e^{n + 1} - \sum_{n = 1}^{\infty} \frac{{(- 1)}^{n - 1}}{{(n + 1)}^{2}} e^{n + 1}

\dots b e c o n t i n u e d \dots