Menu Close

calculate-1-x-cosx-i-1-n-1-tan-2-x-2-i-dx-

Tinku Tara 0 Comments
Pin




Question Number 65092 by mathmax by abdo last updated on 25/Jul/19
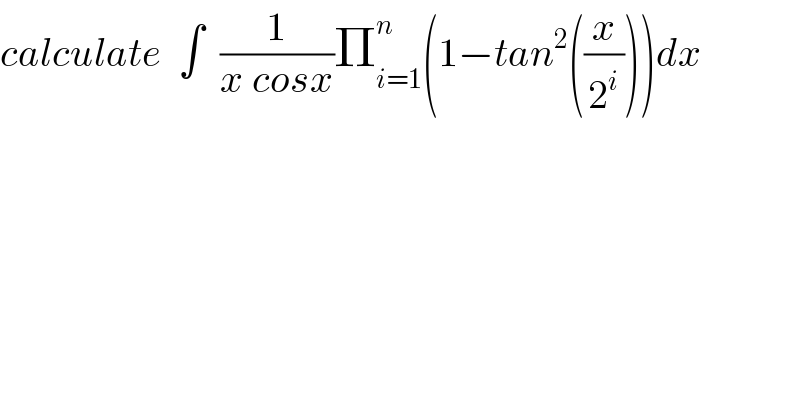
calculate ∫ (1/(x cosx))Π_(i=1) ^n (1−tan^2 ((x/2^i )))dx
$${calculate}\:\:\int\:\:\frac{\mathrm{1}}{{x}\:{cosx}}\prod_{{i}=\mathrm{1}} ^{{n}} \left(\mathrm{1}−{tan}^{\mathrm{2}} \left(\frac{{x}}{\mathrm{2}^{{i}} }\right)\right){dx} \\ $$
Commented by ~ À ® @ 237 ~ last updated on 25/Jul/19
let call it F_n (x).And P_n (x)=Π_(i=1) ^n (1−tan^2 ((x/2^i ))) we know that ∀ i=1.....n 1−tan^2 ((x/2^i ))=((2tan((x/2^i )))/(tan(2.(x/2^i )))) so P_n (x)=2_ ^n Π_(i=1) ^n (((tan((x/2^i )))/(tan((x/2^(i−1) )))))=((2^n tan((x/2^n )))/(tanx)) then F_n (x)=∫ (((2^(n ) tan((x/2^n )))/(xsinx)))dx =? ( i am trying..... But F_∞ (x)=∫(1/(xcosx))P_∞ (x)dx is solvable with P_∞ (x)=lim_∞ P_n (x)=(x/(tanx)) then F_∞ (x)=∫ (1/(xcosx)).(x/(tanx))dx=∫ (1/(sinx))dx=∫ ((cos^2 ((x/2))+sin^2 ((x/2)))/(2sin((x/2))cos((x/2)))) dx =∫ (((1/2)cos((x/2)))/(sin((x/2)))) + (((1/2)sin((x/2)))/(cos((x/2)))) dx=ln∣tan((x/2))∣ +c c∈R
$${let}\:{call}\:{it}\:{F}_{{n}} \left({x}\right).{And}\:\:{P}_{{n}} \left({x}\right)=\underset{{i}=\mathrm{1}} {\overset{{n}} {\prod}}\left(\mathrm{1}−{tan}^{\mathrm{2}} \left(\frac{{x}}{\mathrm{2}^{{i}} }\right)\right) \\ $$$${we}\:{know}\:{that}\:\forall\:{i}=\mathrm{1}…..{n}\:\:\:\mathrm{1}−{tan}^{\mathrm{2}} \left(\frac{{x}}{\mathrm{2}^{{i}} }\right)=\frac{\mathrm{2}{tan}\left(\frac{{x}}{\mathrm{2}^{{i}} }\right)}{{tan}\left(\mathrm{2}.\frac{{x}}{\mathrm{2}^{{i}} }\right)} \\ $$$${so}\:\:{P}_{{n}} \left({x}\right)=\mathrm{2}_{} ^{{n}} \:\underset{{i}=\mathrm{1}} {\overset{{n}} {\prod}}\:\left(\frac{{tan}\left(\frac{{x}}{\mathrm{2}^{{i}} }\right)}{{tan}\left(\frac{{x}}{\mathrm{2}^{{i}−\mathrm{1}} }\right)}\right)=\frac{\mathrm{2}^{{n}} {tan}\left(\frac{{x}}{\mathrm{2}^{{n}} }\right)}{{tanx}} \\ $$$${then}\:\:\:{F}_{{n}} \left({x}\right)=\int\:\left(\frac{\mathrm{2}^{{n}\:} {tan}\left(\frac{{x}}{\mathrm{2}^{{n}} }\right)}{{xsinx}}\right){dx}\:\:=?\:\left(\:{i}\:{am}\:{trying}…..\right. \\ $$$${But}\:\:{F}_{\infty} \left({x}\right)=\int\frac{\mathrm{1}}{{xcosx}}{P}_{\infty} \left({x}\right){dx}\:\:\:{is}\:{solvable}\:{with}\:{P}_{\infty} \left({x}\right)={li}\underset{\infty} {{m}}\:{P}_{{n}} \left({x}\right)=\frac{{x}}{{tanx}} \\ $$$${then} \\ $$$${F}_{\infty} \left({x}\right)=\int\:\:\frac{\mathrm{1}}{{xcosx}}.\frac{{x}}{{tanx}}{dx}=\int\:\frac{\mathrm{1}}{{sinx}}{dx}=\int\:\frac{{cos}^{\mathrm{2}} \left(\frac{{x}}{\mathrm{2}}\right)+{sin}^{\mathrm{2}} \left(\frac{{x}}{\mathrm{2}}\right)}{\mathrm{2}{sin}\left(\frac{{x}}{\mathrm{2}}\right){cos}\left(\frac{{x}}{\mathrm{2}}\right)}\:{dx} \\ $$$$\:\:\:\:\:\:\:\:\:=\int\:\:\frac{\frac{\mathrm{1}}{\mathrm{2}}{cos}\left(\frac{{x}}{\mathrm{2}}\right)}{{sin}\left(\frac{{x}}{\mathrm{2}}\right)}\:+\:\frac{\frac{\mathrm{1}}{\mathrm{2}}{sin}\left(\frac{{x}}{\mathrm{2}}\right)}{{cos}\left(\frac{{x}}{\mathrm{2}}\right)}\:{dx}={ln}\mid{tan}\left(\frac{{x}}{\mathrm{2}}\right)\mid\:+{c}\:\:\:\:\:\:\:{c}\in\mathbb{R} \\ $$
Commented by Prithwish sen last updated on 25/Jul/19
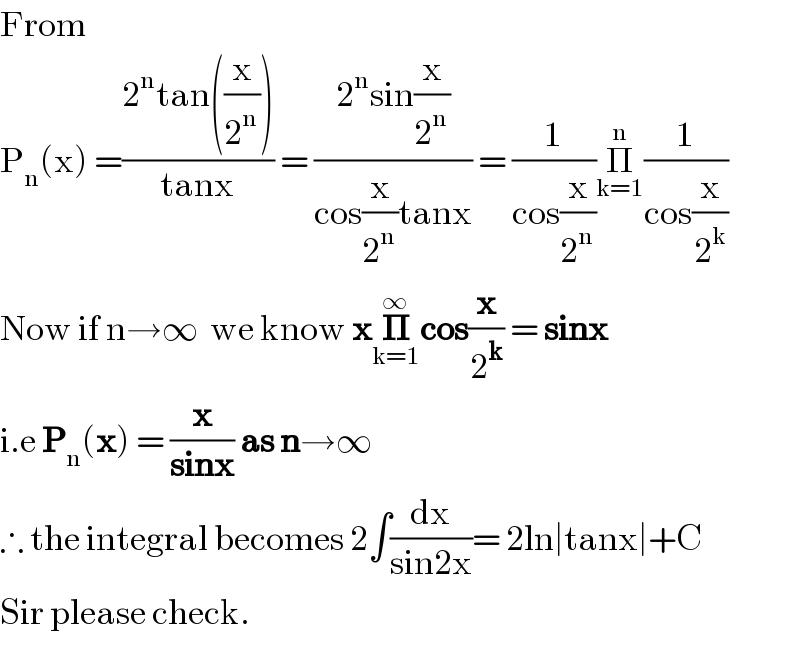
From P_n (x) =((2^n tan((x/2^n )))/(tanx)) = ((2^n sin(x/2^n ))/(cos(x/2^n )tanx)) = (1/(cos(x/2^n )))Π_(k=1) ^n (1/(cos(x/2^k ))) Now if n→∞ we know x𝚷_(k=1) ^∞ cos(x/2^k ) = sinx i.e P_n (x) = (x/(sinx)) as n→∞ ∴ the integral becomes 2∫(dx/(sin2x))= 2ln∣tanx∣+C Sir please check.
$$\mathrm{From} \\ $$$$\mathrm{P}_{\mathrm{n}} \left(\mathrm{x}\right)\:=\frac{\mathrm{2}^{\mathrm{n}} \mathrm{tan}\left(\frac{\mathrm{x}}{\mathrm{2}^{\mathrm{n}} }\right)}{\mathrm{tanx}}\:=\:\frac{\mathrm{2}^{\mathrm{n}} \mathrm{sin}\frac{\mathrm{x}}{\mathrm{2}^{\mathrm{n}} }}{\mathrm{cos}\frac{\mathrm{x}}{\mathrm{2}^{\mathrm{n}} }\mathrm{tanx}}\:=\:\frac{\mathrm{1}}{\mathrm{cos}\frac{\mathrm{x}}{\mathrm{2}^{\mathrm{n}} }}\underset{\mathrm{k}=\mathrm{1}} {\overset{\mathrm{n}} {\prod}}\frac{\mathrm{1}}{\mathrm{cos}\frac{\mathrm{x}}{\mathrm{2}^{\mathrm{k}} }} \\ $$$$\mathrm{Now}\:\mathrm{if}\:\mathrm{n}\rightarrow\infty\:\:\mathrm{we}\:\mathrm{know}\:\boldsymbol{\mathrm{x}}\underset{\mathrm{k}=\mathrm{1}} {\overset{\infty} {\boldsymbol{\prod}}\mathrm{cos}}\frac{\boldsymbol{\mathrm{x}}}{\mathrm{2}^{\boldsymbol{\mathrm{k}}} }\:=\:\boldsymbol{\mathrm{sinx}} \\ $$$$\mathrm{i}.\mathrm{e}\:\boldsymbol{\mathrm{P}}_{\mathrm{n}} \left(\boldsymbol{\mathrm{x}}\right)\:=\:\frac{\boldsymbol{\mathrm{x}}}{\boldsymbol{\mathrm{sinx}}}\:\boldsymbol{\mathrm{as}}\:\boldsymbol{\mathrm{n}}\rightarrow\infty \\ $$$$\therefore\:\mathrm{the}\:\mathrm{integral}\:\mathrm{becomes}\:\mathrm{2}\int\frac{\mathrm{dx}}{\mathrm{sin2x}}=\:\mathrm{2ln}\mid\mathrm{tanx}\mid+\mathrm{C} \\ $$$$\mathrm{Sir}\:\mathrm{please}\:\mathrm{check}. \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *