Question Number 81433 by abdomathmax last updated on 13/Feb/20
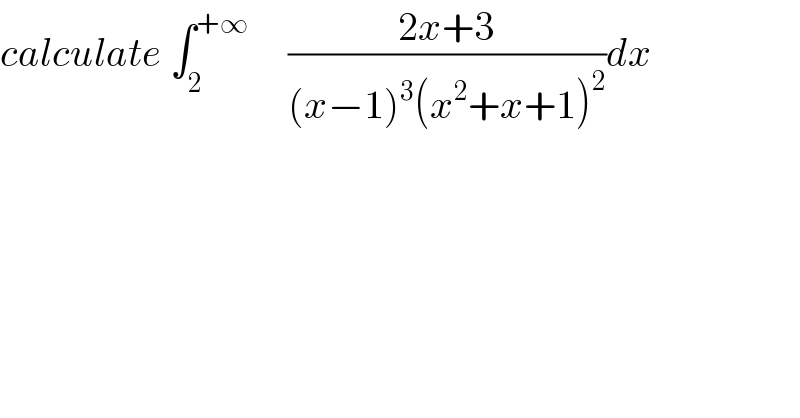
$${calculate}\:\int_{\mathrm{2}} ^{+\infty} \:\:\:\:\:\frac{\mathrm{2}{x}+\mathrm{3}}{\left({x}−\mathrm{1}\right)^{\mathrm{3}} \left({x}^{\mathrm{2}} +{x}+\mathrm{1}\right)^{\mathrm{2}} }{dx} \\ $$
Answered by MJS last updated on 13/Feb/20

$$\int\frac{\mathrm{2}{x}+\mathrm{3}}{\left({x}−\mathrm{1}\right)^{\mathrm{2}} \left({x}^{\mathrm{2}} +{x}+\mathrm{1}\right)^{\mathrm{2}} }= \\ $$$$\:\:\:\:\:{Q}_{\mathrm{1}} \left({x}\right)={Q}_{\mathrm{2}} \left({x}\right)=\left({x}−\mathrm{1}\right)\left({x}^{\mathrm{2}} +{x}+\mathrm{1}\right) \\ $$$$\:\:\:\:\:{P}_{\mathrm{1}} \left({x}\right)=−\frac{\mathrm{2}}{\mathrm{3}}{x}^{\mathrm{2}} −{x} \\ $$$$\:\:\:\:\:{P}_{\mathrm{2}} \left({x}\right)=−\frac{\mathrm{2}}{\mathrm{3}}{x}−\mathrm{2} \\ $$$$=−\frac{{x}\left(\mathrm{2}{x}+\mathrm{3}\right)}{\mathrm{3}\left({x}−\mathrm{1}\right)\left({x}^{\mathrm{2}} +{x}+\mathrm{1}\right)}−\frac{\mathrm{2}}{\mathrm{3}}\int\frac{{x}+\mathrm{3}}{\left({x}−\mathrm{1}\right)\left({x}^{\mathrm{2}} +{x}+\mathrm{1}\right)}{dx}= \\ $$$$\:\:\:\:\:\int\frac{{x}+\mathrm{3}}{\left({x}−\mathrm{1}\right)\left({x}^{\mathrm{2}} +{x}+\mathrm{1}\right)}{dx}=\frac{\mathrm{4}}{\mathrm{3}}\int\frac{{dx}}{{x}−\mathrm{1}}−\frac{\mathrm{1}}{\mathrm{3}}\int\frac{\mathrm{4}{x}+\mathrm{5}}{{x}^{\mathrm{2}} +{x}+\mathrm{1}}{dx}= \\ $$$$\:\:\:\:\:=\frac{\mathrm{4}}{\mathrm{3}}\mathrm{ln}\:\mid{x}−\mathrm{1}\mid\:−\frac{\mathrm{2}}{\mathrm{3}}\mathrm{ln}\:\left({x}^{\mathrm{2}} +{x}+\mathrm{1}\right)\:−\frac{\mathrm{2}\sqrt{\mathrm{3}}}{\mathrm{3}}\mathrm{arctan}\:\frac{\sqrt{\mathrm{3}}\left(\mathrm{2}{x}+\mathrm{1}\right)}{\mathrm{3}}\:= \\ $$$$\:\:\:\:\:=\frac{\mathrm{2}}{\mathrm{3}}\mathrm{ln}\:\frac{\left({x}−\mathrm{1}\right)^{\mathrm{2}} }{{x}^{\mathrm{2}} +{x}+\mathrm{1}}\:−\frac{\mathrm{2}\sqrt{\mathrm{3}}}{\mathrm{3}}\mathrm{arctan}\:\frac{\sqrt{\mathrm{3}}\left(\mathrm{2}{x}+\mathrm{1}\right)}{\mathrm{3}} \\ $$$$=−\frac{{x}\left(\mathrm{2}{x}+\mathrm{3}\right)}{\mathrm{3}\left({x}−\mathrm{1}\right)\left({x}^{\mathrm{2}} +{x}+\mathrm{1}\right)}−\frac{\mathrm{4}}{\mathrm{9}}\mathrm{ln}\:\frac{\left({x}−\mathrm{1}\right)^{\mathrm{2}} }{{x}^{\mathrm{2}} +{x}+\mathrm{1}}\:+\frac{\mathrm{4}\sqrt{\mathrm{3}}}{\mathrm{9}}\mathrm{arctan}\:\frac{\sqrt{\mathrm{3}}\left(\mathrm{2}{x}+\mathrm{1}\right)}{\mathrm{3}}\:+{C} \\ $$$$\Rightarrow \\ $$$$\mathrm{answer}\:\mathrm{is}\:\frac{\mathrm{2}\pi\sqrt{\mathrm{3}}}{\mathrm{9}}+\frac{\mathrm{2}}{\mathrm{3}}−\frac{\mathrm{4}}{\mathrm{9}}\mathrm{ln}\:\mathrm{7}\:−\frac{\mathrm{4}\sqrt{\mathrm{3}}}{\mathrm{9}}\mathrm{arctan}\:\frac{\mathrm{5}\sqrt{\mathrm{3}}}{\mathrm{3}} \\ $$
Commented by john santu last updated on 13/Feb/20

$$\mathrm{Ostrogradski}\:\mathrm{method}.\:\mathrm{i}\:\mathrm{will}\:\mathrm{learn} \\ $$$$\mathrm{this}\:\mathrm{method} \\ $$$$ \\ $$
Commented by abdomathmax last updated on 13/Feb/20
$${thank}\:{you}\:{sir}\:{mjs} \\ $$
