Question Number 45512 by Tawa1 last updated on 13/Oct/18
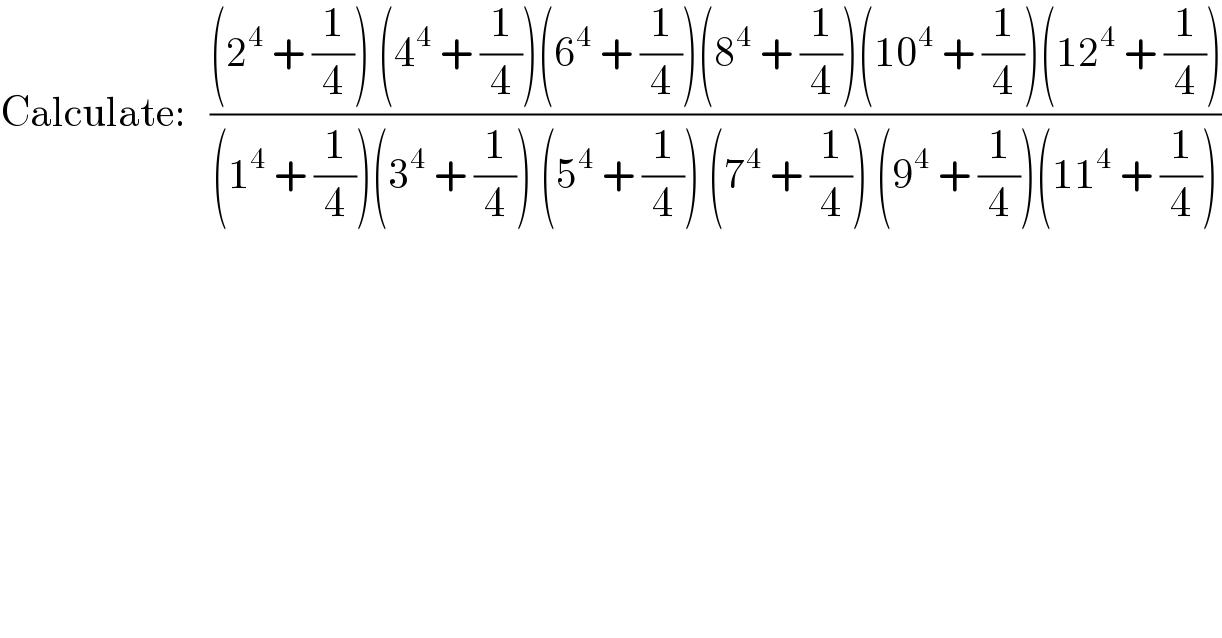
$$\mathrm{Calculate}:\:\:\:\frac{\left(\mathrm{2}^{\mathrm{4}} \:+\:\frac{\mathrm{1}}{\mathrm{4}}\right)\:\left(\mathrm{4}^{\mathrm{4}} \:+\:\frac{\mathrm{1}}{\mathrm{4}}\right)\left(\mathrm{6}^{\mathrm{4}} \:+\:\frac{\mathrm{1}}{\mathrm{4}}\right)\left(\mathrm{8}^{\mathrm{4}} \:+\:\frac{\mathrm{1}}{\mathrm{4}}\right)\left(\mathrm{10}^{\mathrm{4}} \:+\:\frac{\mathrm{1}}{\mathrm{4}}\right)\left(\mathrm{12}^{\mathrm{4}} \:+\:\frac{\mathrm{1}}{\mathrm{4}}\right)}{\left(\mathrm{1}^{\mathrm{4}} \:+\:\frac{\mathrm{1}}{\mathrm{4}}\right)\left(\mathrm{3}^{\mathrm{4}} \:+\:\frac{\mathrm{1}}{\mathrm{4}}\right)\:\left(\mathrm{5}^{\mathrm{4}} \:+\:\frac{\mathrm{1}}{\mathrm{4}}\right)\:\left(\mathrm{7}^{\mathrm{4}} \:+\:\frac{\mathrm{1}}{\mathrm{4}}\right)\:\left(\mathrm{9}^{\mathrm{4}} \:+\:\frac{\mathrm{1}}{\mathrm{4}}\right)\left(\mathrm{11}^{\mathrm{4}} \:+\:\frac{\mathrm{1}}{\mathrm{4}}\right)} \\ $$
Commented by tanmay.chaudhury50@gmail.com last updated on 14/Oct/18

$${excellent}…{sir}… \\ $$
Commented by Meritguide1234 last updated on 14/Oct/18

Commented by Tawa1 last updated on 14/Oct/18

$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir} \\ $$
Commented by Tawa1 last updated on 14/Oct/18
$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir} \\ $$
Commented by Tawa1 last updated on 14/Oct/18
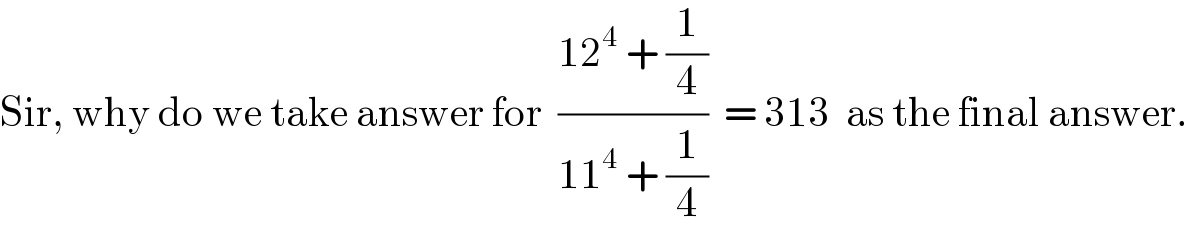
$$\mathrm{Sir},\:\mathrm{why}\:\mathrm{do}\:\mathrm{we}\:\mathrm{take}\:\mathrm{answer}\:\mathrm{for}\:\:\frac{\mathrm{12}^{\mathrm{4}} \:+\:\frac{\mathrm{1}}{\mathrm{4}}}{\mathrm{11}^{\mathrm{4}} \:+\:\frac{\mathrm{1}}{\mathrm{4}}}\:\:=\:\mathrm{313}\:\:\mathrm{as}\:\mathrm{the}\:\mathrm{final}\:\mathrm{answer}. \\ $$
Commented by Meritguide1234 last updated on 14/Oct/18
$${thank}\:{you}\:…{sir} \\ $$
Commented by Meritguide1234 last updated on 14/Oct/18
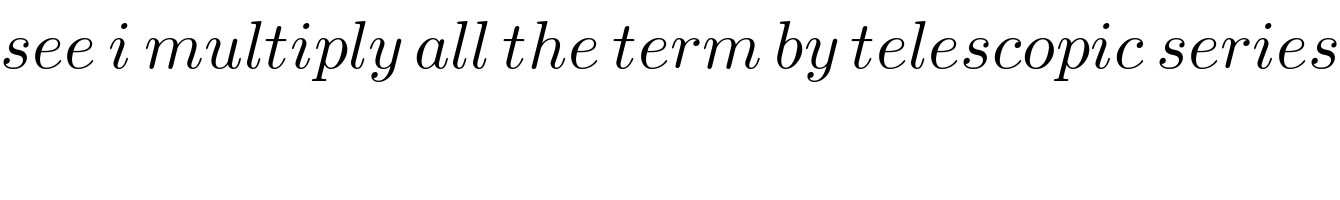
$${see}\:{i}\:{multiply}\:{all}\:{the}\:{term}\:{by}\:{telescopic}\:{series} \\ $$
Commented by Tawa1 last updated on 14/Oct/18

$$\mathrm{Please}\:\mathrm{sir},\:\mathrm{show}\:\mathrm{example}\:\mathrm{of}\:\mathrm{how}\:\mathrm{you}\:\mathrm{multiply}.\:\mathrm{Sorry}\:\mathrm{to}\:\mathrm{be}\:\mathrm{bothering} \\ $$$$\mathrm{you}\:\mathrm{sir},\:\:\mathrm{i}\:\mathrm{just}\:\mathrm{want}\:\mathrm{to}\:\mathrm{understand}\:\mathrm{how}\:\mathrm{you}\:\mathrm{multiply}\:\mathrm{sir} \\ $$
Commented by tanmay.chaudhury50@gmail.com last updated on 14/Oct/18

$$\frac{\mathrm{2}^{\mathrm{4}} +\frac{\mathrm{1}}{\mathrm{4}}}{\mathrm{1}^{\mathrm{4}} +\frac{\mathrm{1}}{\mathrm{4}}}=\frac{\left(\mathrm{2}^{\mathrm{2}} +\mathrm{2}+\frac{\mathrm{1}}{\mathrm{2}}\right)\left(\mathrm{2}^{\mathrm{2}} −\mathrm{2}+\frac{\mathrm{1}}{\mathrm{2}}\right)}{\left(\mathrm{1}^{\mathrm{2}} +\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}}\right)\left(\mathrm{1}^{\mathrm{2}} −\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}}\right)} \\ $$$${now}\:{see}\:{the}\:{red}\:{marked}\:{expression}\:\:{bothare} \\ $$$${same}\:{value}\:\left(\frac{\mathrm{5}}{\mathrm{2}}\right)\:\:{so}\:{they}\:{cancelled}.. \\ $$$$\frac{\mathrm{4}^{\mathrm{4}} +\frac{\mathrm{1}}{\mathrm{4}}}{\mathrm{3}^{\mathrm{4}} +\frac{\mathrm{1}}{\mathrm{4}}}=\frac{\left(\mathrm{4}^{\mathrm{2}} +\mathrm{4}+\frac{\mathrm{1}}{\mathrm{2}}\right)\left(\mathrm{4}^{\mathrm{2}} −\mathrm{4}+\frac{\mathrm{1}}{\mathrm{2}}\right)}{\left(\mathrm{3}^{\mathrm{2}} +\mathrm{3}+\frac{\mathrm{1}}{\mathrm{2}}\right)\left(\mathrm{3}^{\mathrm{2}} −\mathrm{3}+\frac{\mathrm{1}}{\mathrm{2}}\right)} \\ $$$${again}\:{see}\:{red}\:{marked}\:{expfession}\:{cancelled} \\ $$$$\left(\frac{\mathrm{25}}{\mathrm{2}}\right) \\ $$$${thus}\:{resul}\:{obtained}… \\ $$
Commented by Tawa1 last updated on 14/Oct/18
$$\mathrm{Wow},\:\mathrm{i}\:\mathrm{understand}\:\mathrm{now}\:\mathrm{sir}. \\ $$
Commented by Tawa1 last updated on 14/Oct/18

$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir} \\ $$
