Menu Close

Calculate-2-4sin-x-cos-x-1-sin-2x-sin-4-2x-64-cos-4-2x-dx-

Tinku Tara 0 Comments
Pin




Question Number 163008 by tounghoungko last updated on 03/Jan/22
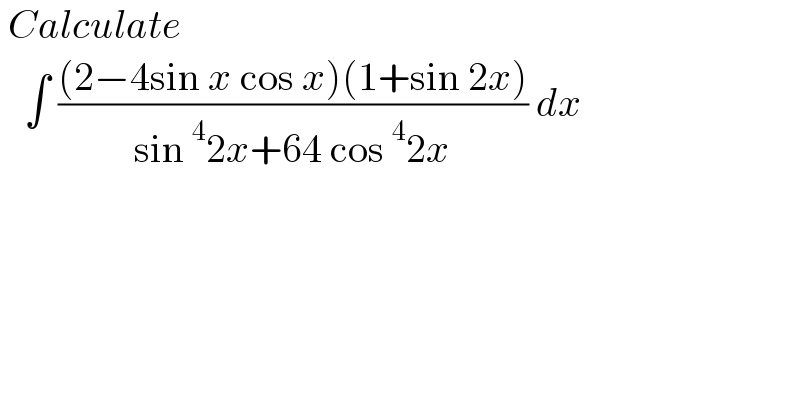
Calculate ∫ (((2−4sin x cos x)(1+sin 2x))/(sin^4 2x+64 cos^4 2x)) dx
$$\:{Calculate}\: \\ $$$$\:\:\:\int\:\frac{\left(\mathrm{2}−\mathrm{4sin}\:{x}\:\mathrm{cos}\:{x}\right)\left(\mathrm{1}+\mathrm{sin}\:\mathrm{2}{x}\right)}{\mathrm{sin}\:^{\mathrm{4}} \mathrm{2}{x}+\mathrm{64}\:\mathrm{cos}\:^{\mathrm{4}} \mathrm{2}{x}}\:{dx}\: \\ $$$$ \\ $$
Answered by som(math1967) last updated on 03/Jan/22
∫((2(1−2sinxcosx)(1+sin2x))/(sin^4 x+64cos^4 x))dx ∫((2(1−sin^2 2x)dx)/(sin^4 x+64cos^4 x)) ∫((2cos^2 2xsec^4 2xdx)/(sec^4 2x(sin^4 2x+64cos^4 2x))) ∫((2sec^2 2xdx)/(tan^4 2x+64)) let tan2x=z ∴2sec^2 2xdx=dz ∫(dz/(z^4 +8^2 )) (1/(16))∫(((8+z^2 )+(8−z^2 )dz)/(z^4 +8^2 )) (1/(16))∫(((8+z^2 )/z^2 )/((z^4 +8^2 )/z^2 ))dz−(1/8)∫(((z^2 −1)/z^2 )/((z^4 +8^2 )/z^2 ))dz (1/(16))∫((d(z−(8/z)))/((z−(8/z))^2 +(4)^2 )) −(1/(16))∫((d(z+(8/z)))/((z+(8/z))^2 −(4)^2 )) (1/(64))tan^(−1) (((z−(1/z))/( 4))) −(1/(128))ln((z+(1/z)−4)/(z+(1/z)+4)) +C z=tan2x
$$\int\frac{\mathrm{2}\left(\mathrm{1}−\mathrm{2}{sinxcosx}\right)\left(\mathrm{1}+{sin}\mathrm{2}{x}\right)}{{sin}^{\mathrm{4}} {x}+\mathrm{64}{cos}^{\mathrm{4}} {x}}{dx} \\ $$$$\int\frac{\mathrm{2}\left(\mathrm{1}−{sin}^{\mathrm{2}} \mathrm{2}{x}\right){dx}}{{sin}^{\mathrm{4}} {x}+\mathrm{64}{cos}^{\mathrm{4}} {x}} \\ $$$$\int\frac{\mathrm{2}{cos}^{\mathrm{2}} \mathrm{2}{xsec}^{\mathrm{4}} \mathrm{2}{xdx}}{{sec}^{\mathrm{4}} \mathrm{2}{x}\left({sin}^{\mathrm{4}} \mathrm{2}{x}+\mathrm{64}{cos}^{\mathrm{4}} \mathrm{2}{x}\right)} \\ $$$$\int\frac{\mathrm{2}{sec}^{\mathrm{2}} \mathrm{2}{xdx}}{{tan}^{\mathrm{4}} \mathrm{2}{x}+\mathrm{64}} \\ $$$${let}\:{tan}\mathrm{2}{x}={z} \\ $$$$\therefore\mathrm{2}{sec}^{\mathrm{2}} \mathrm{2}{xdx}={dz} \\ $$$$\int\frac{{dz}}{{z}^{\mathrm{4}} +\mathrm{8}^{\mathrm{2}} } \\ $$$$\frac{\mathrm{1}}{\mathrm{16}}\int\frac{\left(\mathrm{8}+{z}^{\mathrm{2}} \right)+\left(\mathrm{8}−{z}^{\mathrm{2}} \right){dz}}{{z}^{\mathrm{4}} +\mathrm{8}^{\mathrm{2}} } \\ $$$$\frac{\mathrm{1}}{\mathrm{16}}\int\frac{\frac{\mathrm{8}+{z}^{\mathrm{2}} }{{z}^{\mathrm{2}} }}{\frac{{z}^{\mathrm{4}} +\mathrm{8}^{\mathrm{2}} }{{z}^{\mathrm{2}} }}{dz}−\frac{\mathrm{1}}{\mathrm{8}}\int\frac{\frac{{z}^{\mathrm{2}} −\mathrm{1}}{{z}^{\mathrm{2}} }}{\frac{{z}^{\mathrm{4}} +\mathrm{8}^{\mathrm{2}} }{{z}^{\mathrm{2}} }}{dz} \\ $$$$\frac{\mathrm{1}}{\mathrm{16}}\int\frac{{d}\left({z}−\frac{\mathrm{8}}{{z}}\right)}{\left({z}−\frac{\mathrm{8}}{{z}}\right)^{\mathrm{2}} +\left(\mathrm{4}\right)^{\mathrm{2}} }\:−\frac{\mathrm{1}}{\mathrm{16}}\int\frac{{d}\left({z}+\frac{\mathrm{8}}{{z}}\right)}{\left({z}+\frac{\mathrm{8}}{{z}}\right)^{\mathrm{2}} −\left(\mathrm{4}\right)^{\mathrm{2}} } \\ $$$$\:\frac{\mathrm{1}}{\mathrm{64}}\mathrm{tan}^{−\mathrm{1}} \left(\frac{{z}−\frac{\mathrm{1}}{{z}}}{\:\mathrm{4}}\right)\:−\frac{\mathrm{1}}{\mathrm{128}}{ln}\frac{{z}+\frac{\mathrm{1}}{{z}}−\mathrm{4}}{{z}+\frac{\mathrm{1}}{{z}}+\mathrm{4}}\:+{C} \\ $$$$\:{z}={tan}\mathrm{2}{x} \\ $$
Answered by Ar Brandon last updated on 03/Jan/22
I=∫(((2−4sinxcosx)(1+sin2x))/(sin^4 2x+64cos^4 2x))dx =∫((2(1−sin2x)(1+sin2x))/(sin^4 2x+64cos^4 2x))dx =2∫((1−sin^2 2x)/(sin^4 2x+64cos^4 2x))dx=2∫((sec^2 2x)/(tan^4 2x+64))dx t=tan2x, dt=2sec^2 2xdx =∫(dt/(t^4 +64))=(1/(16))∫(((t^2 +8)−(t^2 −8))/(t^4 +64))dt =(1/(16))∫((1+(8/t^2 ))/((t−(8/t))^2 +16))dt−(1/(16))∫((1−(8/t^2 ))/((t+(8/t))^2 −16))dt =(1/(16))∫(du/(u^2 +16))−(1/(16))∫(dv/(v^2 −16)) =(1/(64))tan^(−1) ((u/( 4)))+(1/(64))tanh^(−1) ((v/( 4)))+C =(1/(64))tan^(−1) (((tan^2 2x−8)/(4tan2x)))+(1/(128))ln(∣((tan^2 2x+4tan2x+8)/(tan^2 2x−4tan2x+8))∣)+C
$${I}=\int\frac{\left(\mathrm{2}−\mathrm{4sin}{x}\mathrm{cos}{x}\right)\left(\mathrm{1}+\mathrm{sin2}{x}\right)}{\mathrm{sin}^{\mathrm{4}} \mathrm{2}{x}+\mathrm{64cos}^{\mathrm{4}} \mathrm{2}{x}}{dx} \\ $$$$\:\:\:=\int\frac{\mathrm{2}\left(\mathrm{1}−\mathrm{sin2}{x}\right)\left(\mathrm{1}+\mathrm{sin2}{x}\right)}{\mathrm{sin}^{\mathrm{4}} \mathrm{2}{x}+\mathrm{64cos}^{\mathrm{4}} \mathrm{2}{x}}{dx} \\ $$$$\:\:\:=\mathrm{2}\int\frac{\mathrm{1}−\mathrm{sin}^{\mathrm{2}} \mathrm{2}{x}}{\mathrm{sin}^{\mathrm{4}} \mathrm{2}{x}+\mathrm{64cos}^{\mathrm{4}} \mathrm{2}{x}}{dx}=\mathrm{2}\int\frac{\mathrm{sec}^{\mathrm{2}} \mathrm{2}{x}}{\mathrm{tan}^{\mathrm{4}} \mathrm{2}{x}+\mathrm{64}}{dx} \\ $$$$\:\:\:\:\:\:\:\:\:{t}=\mathrm{tan2}{x},\:{dt}=\mathrm{2sec}^{\mathrm{2}} \mathrm{2}{xdx} \\ $$$$\:\:\:=\int\frac{{dt}}{{t}^{\mathrm{4}} +\mathrm{64}}=\frac{\mathrm{1}}{\mathrm{16}}\int\frac{\left({t}^{\mathrm{2}} +\mathrm{8}\right)−\left({t}^{\mathrm{2}} −\mathrm{8}\right)}{{t}^{\mathrm{4}} +\mathrm{64}}{dt} \\ $$$$\:\:\:=\frac{\mathrm{1}}{\mathrm{16}}\int\frac{\mathrm{1}+\frac{\mathrm{8}}{{t}^{\mathrm{2}} }}{\left({t}−\frac{\mathrm{8}}{{t}}\right)^{\mathrm{2}} +\mathrm{16}}{dt}−\frac{\mathrm{1}}{\mathrm{16}}\int\frac{\mathrm{1}−\frac{\mathrm{8}}{{t}^{\mathrm{2}} }}{\left({t}+\frac{\mathrm{8}}{{t}}\right)^{\mathrm{2}} −\mathrm{16}}{dt} \\ $$$$\:\:\:=\frac{\mathrm{1}}{\mathrm{16}}\int\frac{{du}}{{u}^{\mathrm{2}} +\mathrm{16}}−\frac{\mathrm{1}}{\mathrm{16}}\int\frac{{d}\mathrm{v}}{\mathrm{v}^{\mathrm{2}} −\mathrm{16}} \\ $$$$\:\:\:=\frac{\mathrm{1}}{\mathrm{64}}\mathrm{tan}^{−\mathrm{1}} \left(\frac{{u}}{\:\mathrm{4}}\right)+\frac{\mathrm{1}}{\mathrm{64}}\mathrm{tanh}^{−\mathrm{1}} \left(\frac{\mathrm{v}}{\:\mathrm{4}}\right)+{C} \\ $$$$\:\:\:=\frac{\mathrm{1}}{\mathrm{64}}\mathrm{tan}^{−\mathrm{1}} \left(\frac{\mathrm{tan}^{\mathrm{2}} \mathrm{2}{x}−\mathrm{8}}{\mathrm{4tan2}{x}}\right)+\frac{\mathrm{1}}{\mathrm{128}}\mathrm{ln}\left(\mid\frac{\mathrm{tan}^{\mathrm{2}} \mathrm{2}{x}+\mathrm{4tan2}{x}+\mathrm{8}}{\mathrm{tan}^{\mathrm{2}} \mathrm{2}{x}−\mathrm{4tan2}{x}+\mathrm{8}}\mid\right)+{C} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *