Question Number 126873 by mathmax by abdo last updated on 25/Dec/20
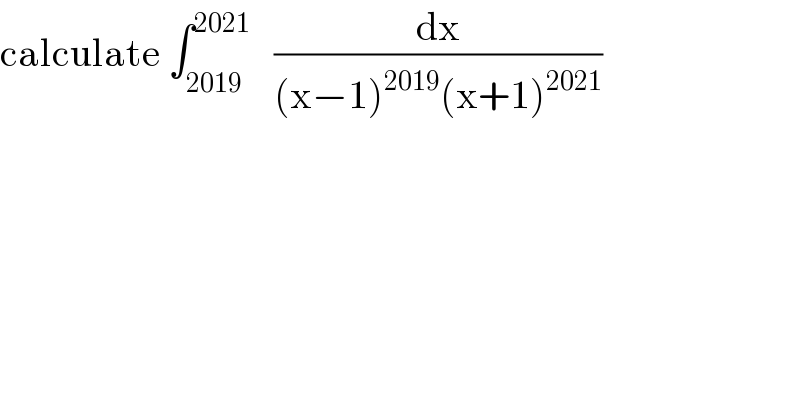
$$\mathrm{calculate}\:\int_{\mathrm{2019}} ^{\mathrm{2021}} \:\:\:\frac{\mathrm{dx}}{\left(\mathrm{x}−\mathrm{1}\right)^{\mathrm{2019}} \left(\mathrm{x}+\mathrm{1}\right)^{\mathrm{2021}} } \\ $$
Answered by Ar Brandon last updated on 25/Dec/20
![I=∫_(2019) ^(2021) (dx/((x−1)^(2019) (x+1)^(2021) )) =∫_(2019) ^(2021) (((x−1)^2 )/((x−1)^(2021) (x+1)^(2021) ))dx =∫_(2019) ^(2021) ((x^2 −2x+1)/((x^2 −1)^(2021) ))dx x^2 −2x+1=λ(x^2 −1)+μ{(d/dx)(x^2 −1)}+γ =λ(x^2 −1)+μ(2x)+γ λ=1, μ=−1, −λ+γ=1, γ=2 I=∫_(2019) ^(2021) {((x^2 −1)/((x^2 −1)^(2021) ))−((2x)/((x^2 −1)^(2021) ))+(2/((x^2 −1)^(2021) ))}dx =[(1/((x^2 −1)^(2020) ))]_(2019) ^(2021) +∫_(2019) ^(2021) {((x^2 −1)/((x^2 −1)^(2021) ))+(2/((x^2 −1)^(2021) ))}dx f(a)=∫(dx/(x^2 −a^2 ))=−(1/a)Arctanh((x/a))+C f ′(a)=∫((2a)/((x^2 −a^2 )^2 )) ...](https://www.tinkutara.com/question/Q126875.png)
$$\mathcal{I}=\int_{\mathrm{2019}} ^{\mathrm{2021}} \frac{\mathrm{dx}}{\left(\mathrm{x}−\mathrm{1}\right)^{\mathrm{2019}} \left(\mathrm{x}+\mathrm{1}\right)^{\mathrm{2021}} } \\ $$$$\:\:\:=\int_{\mathrm{2019}} ^{\mathrm{2021}} \frac{\left(\mathrm{x}−\mathrm{1}\right)^{\mathrm{2}} }{\left(\mathrm{x}−\mathrm{1}\right)^{\mathrm{2021}} \left(\mathrm{x}+\mathrm{1}\right)^{\mathrm{2021}} }\mathrm{dx} \\ $$$$\:\:\:=\int_{\mathrm{2019}} ^{\mathrm{2021}} \frac{\mathrm{x}^{\mathrm{2}} −\mathrm{2x}+\mathrm{1}}{\left(\mathrm{x}^{\mathrm{2}} −\mathrm{1}\right)^{\mathrm{2021}} }\mathrm{dx} \\ $$$$\mathrm{x}^{\mathrm{2}} −\mathrm{2x}+\mathrm{1}=\lambda\left(\mathrm{x}^{\mathrm{2}} −\mathrm{1}\right)+\mu\left\{\frac{\mathrm{d}}{\mathrm{dx}}\left(\mathrm{x}^{\mathrm{2}} −\mathrm{1}\right)\right\}+\gamma \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\lambda\left(\mathrm{x}^{\mathrm{2}} −\mathrm{1}\right)+\mu\left(\mathrm{2x}\right)+\gamma \\ $$$$\lambda=\mathrm{1},\:\mu=−\mathrm{1},\:−\lambda+\gamma=\mathrm{1},\:\gamma=\mathrm{2} \\ $$$$\mathcal{I}=\int_{\mathrm{2019}} ^{\mathrm{2021}} \left\{\frac{\mathrm{x}^{\mathrm{2}} −\mathrm{1}}{\left(\mathrm{x}^{\mathrm{2}} −\mathrm{1}\right)^{\mathrm{2021}} }−\frac{\mathrm{2x}}{\left(\mathrm{x}^{\mathrm{2}} −\mathrm{1}\right)^{\mathrm{2021}} }+\frac{\mathrm{2}}{\left(\mathrm{x}^{\mathrm{2}} −\mathrm{1}\right)^{\mathrm{2021}} }\right\}\mathrm{dx} \\ $$$$\:\:=\left[\frac{\mathrm{1}}{\left(\mathrm{x}^{\mathrm{2}} −\mathrm{1}\right)^{\mathrm{2020}} }\right]_{\mathrm{2019}} ^{\mathrm{2021}} +\int_{\mathrm{2019}} ^{\mathrm{2021}} \left\{\frac{\mathrm{x}^{\mathrm{2}} −\mathrm{1}}{\left(\mathrm{x}^{\mathrm{2}} −\mathrm{1}\right)^{\mathrm{2021}} }+\frac{\mathrm{2}}{\left(\mathrm{x}^{\mathrm{2}} −\mathrm{1}\right)^{\mathrm{2021}} }\right\}\mathrm{dx} \\ $$$$\mathrm{f}\left(\mathrm{a}\right)=\int\frac{\mathrm{dx}}{\mathrm{x}^{\mathrm{2}} −\mathrm{a}^{\mathrm{2}} }=−\frac{\mathrm{1}}{\mathrm{a}}\mathrm{Arctanh}\left(\frac{\mathrm{x}}{\mathrm{a}}\right)+\mathcal{C} \\ $$$$\mathrm{f}\:'\left(\mathrm{a}\right)=\int\frac{\mathrm{2a}}{\left(\mathrm{x}^{\mathrm{2}} −\mathrm{a}^{\mathrm{2}} \right)^{\mathrm{2}} } \\ $$$$… \\ $$
Answered by mindispower last updated on 25/Dec/20
![=∫_(2019) ^(2021) (dx/((x+1)^2 (((x−1)/(x+1)))^(2019) )) t=((x−1)/(x+1))⇒dt=(2/((x+1)^2 ))dx ⇔(1/2)∫_((2018)/(2020)) ^((2020)/(2022)) (dt/t^(2019) )=(1/(2(−2018)))[(((2020)/(2022)))^(−2018) −(((2018)/(2020)))^(−2018) ]](https://www.tinkutara.com/question/Q126897.png)
$$=\int_{\mathrm{2019}} ^{\mathrm{2021}} \frac{{dx}}{\left({x}+\mathrm{1}\right)^{\mathrm{2}} \left(\frac{{x}−\mathrm{1}}{{x}+\mathrm{1}}\right)^{\mathrm{2019}} } \\ $$$${t}=\frac{{x}−\mathrm{1}}{{x}+\mathrm{1}}\Rightarrow{dt}=\frac{\mathrm{2}}{\left({x}+\mathrm{1}\right)^{\mathrm{2}} }{dx} \\ $$$$\Leftrightarrow\frac{\mathrm{1}}{\mathrm{2}}\int_{\frac{\mathrm{2018}}{\mathrm{2020}}} ^{\frac{\mathrm{2020}}{\mathrm{2022}}} \frac{{dt}}{{t}^{\mathrm{2019}} }=\frac{\mathrm{1}}{\mathrm{2}\left(−\mathrm{2018}\right)}\left[\left(\frac{\mathrm{2020}}{\mathrm{2022}}\right)^{−\mathrm{2018}} −\left(\frac{\mathrm{2018}}{\mathrm{2020}}\right)^{−\mathrm{2018}} \right] \\ $$$$ \\ $$
Commented by mathmax by abdo last updated on 27/Dec/20

$$\mathrm{not}\:\mathrm{correct}\:\mathrm{sir}\:\mathrm{mind}! \\ $$
Answered by mathmax by abdo last updated on 27/Dec/20
![I =∫_(2019) ^(2021) (dx/((x−1)^(2019) (x+1)^(2021) )) ⇒I =∫_(2019) ^(2021) (dx/((((x−1)/(x+1)))^(2019) (x+1)^(2021+2019) )) we do the changement ((x−1)/(x+1))=t ⇒x−1=tx+t ⇒(1−t)x=t+1 ⇒ x=((1+t)/(1−t)) ⇒(dx/dt)=((1−t−(1+t)(−1))/((1−t)^2 ))=(2/((1−t)^2 )) and x+1=((1+t)/(1−t))+1=((1+t+1−t)/(1−t))=(2/(1−t)) I =∫_(−((1010)/(1009))) ^(−((1011)/(1010))) (2/((1−t)^2 ×t^(2019) ((2/(1−t)))^(2021+2019) ))dt =(2/2^(4040) ) ∫_(−((1010)/(1009))) ^(−((1011)/(1010))) (((1−t)^(4040) )/((1−t)^2 t^(2019) ))dt =(1/2^(4039) )∫_(−((1010)/(1009))) ^(−((1011)/(1010))) (((t−1)^(4038) )/t^(2019) )dt =(1/2^(4039) )∫_(−((1010)/(1009))) ^(−((1011)/(1010))) ((Σ_(k=0) ^(4038) C_(4038) ^k t^k (−1)^(4038−k) )/t^(2019) )dt =(1/2^(4039) )Σ_(k=0) ^(4038) (−1)^k C_(4038) ^k ∫_(−((1010)/(1009))) ^(−((1011)/(1010))) t^(k−2019) dt =(1/2^(4039) ) Σ_(k=0 and k≠2018) ^(4038) (((−1)^k C_(4038) ^k )/(k−2018))[ t^(k−2018) ]_(−((1010)/(1009))) ^(−((1011)/(1010))) +(1/2^(4039) )C_(4038) ^(2018) {ln(((1011)/(1010)))−ln(((1010)/(1009)))} ⇒ I =(1/2^(4039) ) Σ_(k=0 andk≠2018) ^(4038) (((−1)^k C_(4038) ^k )/(k−2018)){(−((1011)/(1010)))^(k−2018) −(−((1010)/(1009)))^(k−2018) } +(1/2^(4039) ) C_(4038) ^(2018) {ln(((1011)/(1010)))−ln(((1010)/(1009)))}](https://www.tinkutara.com/question/Q127208.png)
$$\mathrm{I}\:=\int_{\mathrm{2019}} ^{\mathrm{2021}} \:\frac{\mathrm{dx}}{\left(\mathrm{x}−\mathrm{1}\right)^{\mathrm{2019}} \left(\mathrm{x}+\mathrm{1}\right)^{\mathrm{2021}} }\:\Rightarrow\mathrm{I}\:=\int_{\mathrm{2019}} ^{\mathrm{2021}} \:\frac{\mathrm{dx}}{\left(\frac{\mathrm{x}−\mathrm{1}}{\mathrm{x}+\mathrm{1}}\right)^{\mathrm{2019}} \left(\mathrm{x}+\mathrm{1}\right)^{\mathrm{2021}+\mathrm{2019}} } \\ $$$$\mathrm{we}\:\mathrm{do}\:\mathrm{the}\:\mathrm{changement}\:\frac{\mathrm{x}−\mathrm{1}}{\mathrm{x}+\mathrm{1}}=\mathrm{t}\:\Rightarrow\mathrm{x}−\mathrm{1}=\mathrm{tx}+\mathrm{t}\:\Rightarrow\left(\mathrm{1}−\mathrm{t}\right)\mathrm{x}=\mathrm{t}+\mathrm{1}\:\Rightarrow \\ $$$$\mathrm{x}=\frac{\mathrm{1}+\mathrm{t}}{\mathrm{1}−\mathrm{t}}\:\Rightarrow\frac{\mathrm{dx}}{\mathrm{dt}}=\frac{\mathrm{1}−\mathrm{t}−\left(\mathrm{1}+\mathrm{t}\right)\left(−\mathrm{1}\right)}{\left(\mathrm{1}−\mathrm{t}\right)^{\mathrm{2}} }=\frac{\mathrm{2}}{\left(\mathrm{1}−\mathrm{t}\right)^{\mathrm{2}} }\:\mathrm{and}\:\mathrm{x}+\mathrm{1}=\frac{\mathrm{1}+\mathrm{t}}{\mathrm{1}−\mathrm{t}}+\mathrm{1}=\frac{\mathrm{1}+\mathrm{t}+\mathrm{1}−\mathrm{t}}{\mathrm{1}−\mathrm{t}}=\frac{\mathrm{2}}{\mathrm{1}−\mathrm{t}} \\ $$$$\mathrm{I}\:=\int_{−\frac{\mathrm{1010}}{\mathrm{1009}}} ^{−\frac{\mathrm{1011}}{\mathrm{1010}}} \:\:\:\:\frac{\mathrm{2}}{\left(\mathrm{1}−\mathrm{t}\right)^{\mathrm{2}} ×\mathrm{t}^{\mathrm{2019}} \left(\frac{\mathrm{2}}{\mathrm{1}−\mathrm{t}}\right)^{\mathrm{2021}+\mathrm{2019}} }\mathrm{dt} \\ $$$$=\frac{\mathrm{2}}{\mathrm{2}^{\mathrm{4040}} }\:\int_{−\frac{\mathrm{1010}}{\mathrm{1009}}} ^{−\frac{\mathrm{1011}}{\mathrm{1010}}} \:\:\:\:\frac{\left(\mathrm{1}−\mathrm{t}\right)^{\mathrm{4040}} }{\left(\mathrm{1}−\mathrm{t}\right)^{\mathrm{2}} \:\mathrm{t}^{\mathrm{2019}} }\mathrm{dt} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{4039}} }\int_{−\frac{\mathrm{1010}}{\mathrm{1009}}} ^{−\frac{\mathrm{1011}}{\mathrm{1010}}} \:\:\frac{\left(\mathrm{t}−\mathrm{1}\right)^{\mathrm{4038}} }{\mathrm{t}^{\mathrm{2019}} }\mathrm{dt}\:=\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{4039}} }\int_{−\frac{\mathrm{1010}}{\mathrm{1009}}} ^{−\frac{\mathrm{1011}}{\mathrm{1010}}} \frac{\sum_{\mathrm{k}=\mathrm{0}} ^{\mathrm{4038}} \mathrm{C}_{\mathrm{4038}} ^{\mathrm{k}} \:\mathrm{t}^{\mathrm{k}} \left(−\mathrm{1}\right)^{\mathrm{4038}−\mathrm{k}} }{\mathrm{t}^{\mathrm{2019}} }\mathrm{dt} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{4039}} }\sum_{\mathrm{k}=\mathrm{0}} ^{\mathrm{4038}} \:\left(−\mathrm{1}\right)^{\mathrm{k}} \:\mathrm{C}_{\mathrm{4038}} ^{\mathrm{k}} \:\int_{−\frac{\mathrm{1010}}{\mathrm{1009}}} ^{−\frac{\mathrm{1011}}{\mathrm{1010}}} \mathrm{t}^{\mathrm{k}−\mathrm{2019}} \:\mathrm{dt} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{4039}} }\:\sum_{\mathrm{k}=\mathrm{0}\:\mathrm{and}\:\mathrm{k}\neq\mathrm{2018}} ^{\mathrm{4038}} \:\frac{\left(−\mathrm{1}\right)^{\mathrm{k}} \mathrm{C}_{\mathrm{4038}} ^{\mathrm{k}} }{\mathrm{k}−\mathrm{2018}}\left[\:\mathrm{t}^{\mathrm{k}−\mathrm{2018}} \right]_{−\frac{\mathrm{1010}}{\mathrm{1009}}} ^{−\frac{\mathrm{1011}}{\mathrm{1010}}} \\ $$$$+\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{4039}} }\mathrm{C}_{\mathrm{4038}} ^{\mathrm{2018}} \:\left\{\mathrm{ln}\left(\frac{\mathrm{1011}}{\mathrm{1010}}\right)−\mathrm{ln}\left(\frac{\mathrm{1010}}{\mathrm{1009}}\right)\right\}\:\Rightarrow \\ $$$$\mathrm{I}\:=\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{4039}} }\:\sum_{\mathrm{k}=\mathrm{0}\:\mathrm{andk}\neq\mathrm{2018}} ^{\mathrm{4038}} \:\:\:\frac{\left(−\mathrm{1}\right)^{\mathrm{k}} \:\mathrm{C}_{\mathrm{4038}} ^{\mathrm{k}} }{\mathrm{k}−\mathrm{2018}}\left\{\left(−\frac{\mathrm{1011}}{\mathrm{1010}}\right)^{\mathrm{k}−\mathrm{2018}} −\left(−\frac{\mathrm{1010}}{\mathrm{1009}}\right)^{\mathrm{k}−\mathrm{2018}} \right\} \\ $$$$+\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{4039}} }\:\mathrm{C}_{\mathrm{4038}} ^{\mathrm{2018}} \left\{\mathrm{ln}\left(\frac{\mathrm{1011}}{\mathrm{1010}}\right)−\mathrm{ln}\left(\frac{\mathrm{1010}}{\mathrm{1009}}\right)\right\} \\ $$$$ \\ $$
