Question Number 35686 by prof Abdo imad last updated on 22/May/18
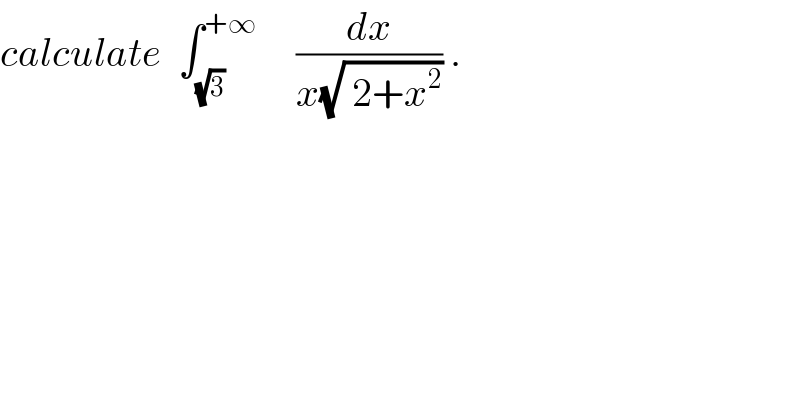
$${calculate}\:\:\int_{\sqrt{\mathrm{3}}} ^{+\infty} \:\:\:\:\:\frac{{dx}}{{x}\sqrt{\:\mathrm{2}+{x}^{\mathrm{2}} }}\:. \\ $$
Commented by prof Abdo imad last updated on 22/May/18
![let put I = ∫_(√3) ^(+∞) (dx/(x(√(2+x^2 )))) changement x=(√2)sh(t) give t =argsh((x/( (√2)))) and I = ∫_(argsh(((√3)/( (√2))))) ^(+∞) (((√2)ch(t)dt)/( (√2)sh(t)(√2)(√(1+sht^2 )))) = ∫_(ln(((√3)/( (√2))) +(√(1 +(3/2))))) ^(+∞) (dt/( (√2)sh(t))) =(1/( (√2))) ∫_(ln( (((√3) +(√5))/( (√2))))) ^(+∞) 2(dt/(e^t −e^(−t) )) =(√2) ∫_(ln((((√3) +(√5))/( (√2))))) ^(+∞) (dt/(e^t −e^(−t) )) =_(e^t =x) (√2) ∫_(((√3)+(√5))/( (√2))) ^(+∞) (1/(x−(1/x))) (dx/x) I = (√2) ∫_(((√3) +(√5))/( (√2))) ^(+∞) (dx/(x^2 −1)) =((√2)/2) ∫_(((√3)+(√5))/( (√2))) ^(+∞) { (1/(x−1)) −(1/(x+1))}dx =((√2)/2)[ln∣((x−1)/(x+1))∣]_(((√3) +(√5))/( (√2))) ^(+∞) =−((√2)/2)ln((((((√3)+(√5))/( (√2)))−1)/((((√3)+(√5))/( (√2)))+1))) =−((√2)/2) ln((((√3) +(√5) −(√2))/( (√3) +(√5) +(√2))))](https://www.tinkutara.com/question/Q35730.png)
$${let}\:{put}\:{I}\:\:=\:\int_{\sqrt{\mathrm{3}}} ^{+\infty} \:\:\:\:\:\frac{{dx}}{{x}\sqrt{\mathrm{2}+{x}^{\mathrm{2}} }}\:\:{changement} \\ $$$${x}=\sqrt{\mathrm{2}}{sh}\left({t}\right)\:{give}\:\:{t}\:={argsh}\left(\frac{{x}}{\:\sqrt{\mathrm{2}}}\right)\:{and} \\ $$$${I}\:=\:\int_{{argsh}\left(\frac{\sqrt{\mathrm{3}}}{\:\sqrt{\mathrm{2}}}\right)} ^{+\infty} \:\frac{\sqrt{\mathrm{2}}{ch}\left({t}\right){dt}}{\:\sqrt{\mathrm{2}}{sh}\left({t}\right)\sqrt{\mathrm{2}}\sqrt{\mathrm{1}+{sht}^{\mathrm{2}} }} \\ $$$$=\:\int_{{ln}\left(\frac{\sqrt{\mathrm{3}}}{\:\sqrt{\mathrm{2}}}\:\:+\sqrt{\mathrm{1}\:\:+\frac{\mathrm{3}}{\mathrm{2}}}\right)} ^{+\infty} \:\:\:\:\:\:\frac{{dt}}{\:\sqrt{\mathrm{2}}{sh}\left({t}\right)} \\ $$$$=\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\:\int_{{ln}\left(\:\frac{\sqrt{\mathrm{3}}\:+\sqrt{\mathrm{5}}}{\:\sqrt{\mathrm{2}}}\right)} ^{+\infty} \:\:\:\:\:\mathrm{2}\frac{{dt}}{{e}^{{t}} \:−{e}^{−{t}} } \\ $$$$=\sqrt{\mathrm{2}}\:\int_{{ln}\left(\frac{\sqrt{\mathrm{3}}\:+\sqrt{\mathrm{5}}}{\:\sqrt{\mathrm{2}}}\right)} ^{+\infty} \:\:\:\:\:\frac{{dt}}{{e}^{{t}} \:−{e}^{−{t}} } \\ $$$$=_{{e}^{{t}} ={x}} \:\:\:\:\sqrt{\mathrm{2}}\:\int_{\frac{\sqrt{\mathrm{3}}+\sqrt{\mathrm{5}}}{\:\sqrt{\mathrm{2}}}} ^{+\infty} \:\:\:\:\:\:\frac{\mathrm{1}}{{x}−\frac{\mathrm{1}}{{x}}}\:\frac{{dx}}{{x}} \\ $$$${I}\:=\:\sqrt{\mathrm{2}}\:\int_{\frac{\sqrt{\mathrm{3}}\:+\sqrt{\mathrm{5}}}{\:\sqrt{\mathrm{2}}}} ^{+\infty} \:\:\:\:\:\frac{{dx}}{{x}^{\mathrm{2}} \:−\mathrm{1}} \\ $$$$=\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\:\int_{\frac{\sqrt{\mathrm{3}}+\sqrt{\mathrm{5}}}{\:\sqrt{\mathrm{2}}}} ^{+\infty} \:\:\left\{\:\frac{\mathrm{1}}{{x}−\mathrm{1}}\:−\frac{\mathrm{1}}{{x}+\mathrm{1}}\right\}{dx} \\ $$$$=\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\left[{ln}\mid\frac{{x}−\mathrm{1}}{{x}+\mathrm{1}}\mid\right]_{\frac{\sqrt{\mathrm{3}}\:+\sqrt{\mathrm{5}}}{\:\sqrt{\mathrm{2}}}} ^{+\infty} \:=−\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}{ln}\left(\frac{\frac{\sqrt{\mathrm{3}}+\sqrt{\mathrm{5}}}{\:\sqrt{\mathrm{2}}}−\mathrm{1}}{\frac{\sqrt{\mathrm{3}}+\sqrt{\mathrm{5}}}{\:\sqrt{\mathrm{2}}}+\mathrm{1}}\right) \\ $$$$=−\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\:{ln}\left(\frac{\sqrt{\mathrm{3}}\:+\sqrt{\mathrm{5}}\:−\sqrt{\mathrm{2}}}{\:\sqrt{\mathrm{3}}\:+\sqrt{\mathrm{5}}\:+\sqrt{\mathrm{2}}}\right) \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 22/May/18
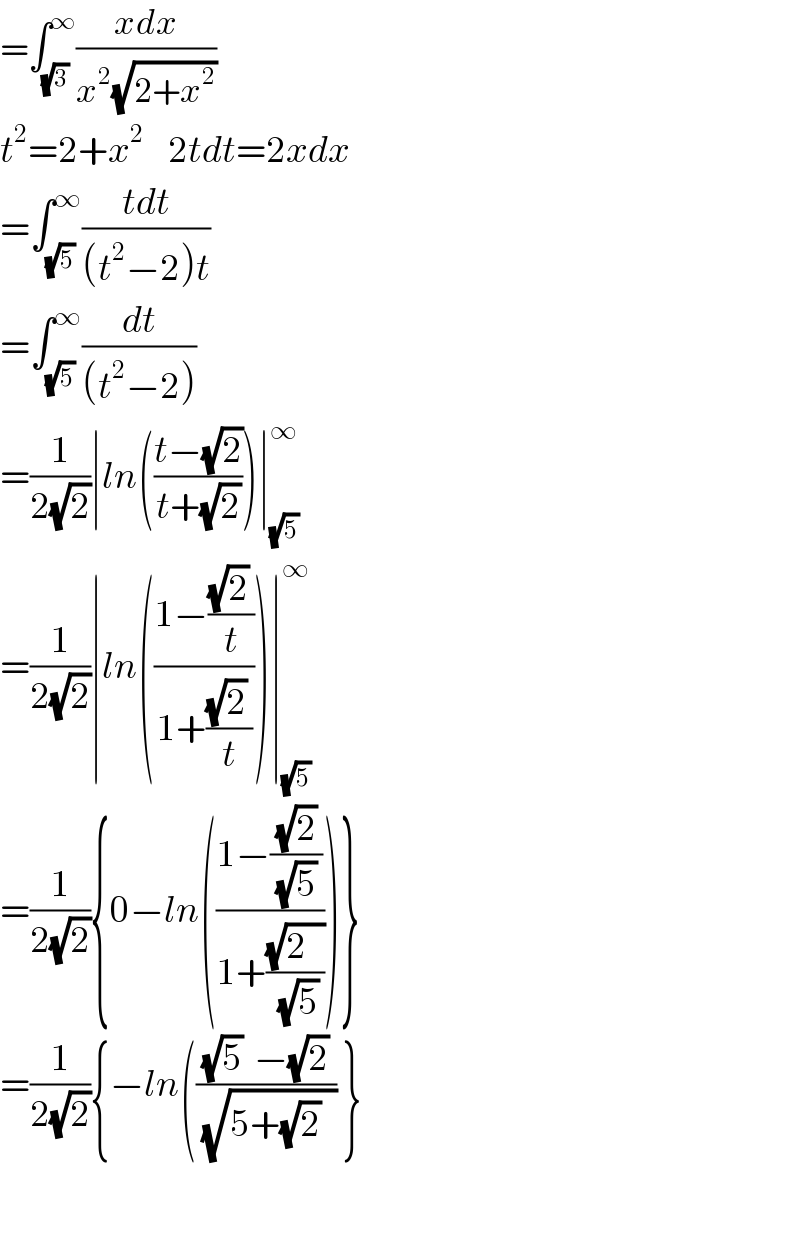
$$=\int_{\sqrt{\mathrm{3}}} ^{\infty} \frac{{xdx}}{{x}^{\mathrm{2}} \sqrt{\mathrm{2}+{x}^{\mathrm{2}} }} \\ $$$${t}^{\mathrm{2}} =\mathrm{2}+{x}^{\mathrm{2}} \:\:\:\:\mathrm{2}{tdt}=\mathrm{2}{xdx} \\ $$$$=\int_{\sqrt{\mathrm{5}}} ^{\infty} \frac{{tdt}}{\left({t}^{\mathrm{2}} −\mathrm{2}\right){t}} \\ $$$$=\int_{\sqrt{\mathrm{5}}} ^{\infty} \frac{{dt}}{\left({t}^{\mathrm{2}} −\mathrm{2}\right)} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{2}}}\mid{ln}\left(\frac{{t}−\sqrt{\mathrm{2}}}{{t}+\sqrt{\mathrm{2}}}\right)\mid_{\sqrt{\mathrm{5}}} ^{\infty} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{2}}}\mid{ln}\left(\frac{\mathrm{1}−\frac{\sqrt{\mathrm{2}}\:}{{t}}}{\mathrm{1}+\frac{\sqrt{\mathrm{2}}\:}{{t}}}\right)\mid_{\sqrt{\mathrm{5}}} ^{\infty} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{2}}}\left\{\mathrm{0}−{ln}\left(\frac{\mathrm{1}−\frac{\sqrt{\mathrm{2}}}{\:\sqrt{\mathrm{5}}\:}}{\mathrm{1}+\frac{\sqrt{\mathrm{2}\:\:\:}}{\:\sqrt{\mathrm{5}}}}\right)\right\} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{2}}}\left\{−{ln}\left(\frac{\sqrt{\mathrm{5}}\:\:−\sqrt{\mathrm{2}}}{\:\sqrt{\mathrm{5}+\sqrt{\mathrm{2}}\:_{} }}\:\right\}\right. \\ $$$$ \\ $$
