Question Number 94905 by mathmax by abdo last updated on 21/May/20
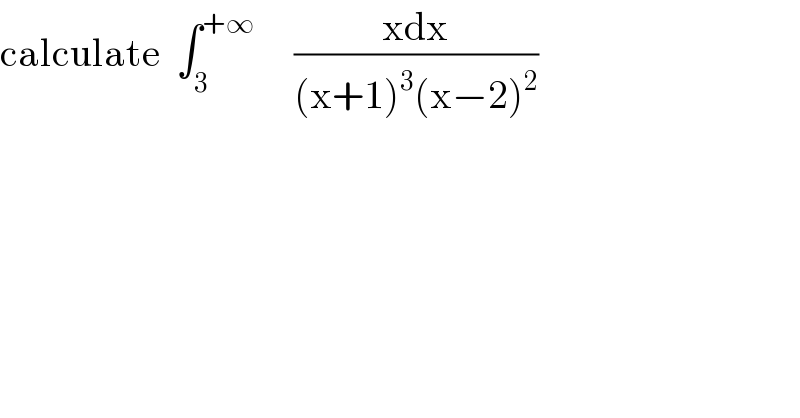
$$\mathrm{calculate}\:\:\int_{\mathrm{3}} ^{+\infty} \:\:\:\:\:\frac{\mathrm{xdx}}{\left(\mathrm{x}+\mathrm{1}\right)^{\mathrm{3}} \left(\mathrm{x}−\mathrm{2}\right)^{\mathrm{2}} } \\ $$
Answered by MJS last updated on 22/May/20
![∫(x/((x+1)^3 (x−2)^2 ))dx= [Ostrogradski] =−((2x^2 +x+2)/(18(x−2)(x+1)^2 ))−(1/9)∫(dx/((x−2)(x+1))) −(1/9)∫(dx/((x−2)(x+1)))= =(1/(27))∫(dx/(x+1))−(1/(27))∫(dx/(x−2))=(1/(27))ln ((x+1)/(x−2)) +C ∫_3 ^∞ (x/((x+1)^3 (x−2)^2 ))dx=((23)/(288))−(2/(27))ln 2](https://www.tinkutara.com/question/Q94990.png)
$$\int\frac{{x}}{\left({x}+\mathrm{1}\right)^{\mathrm{3}} \left({x}−\mathrm{2}\right)^{\mathrm{2}} }{dx}= \\ $$$$\:\:\:\:\:\left[\mathrm{Ostrogradski}\right] \\ $$$$=−\frac{\mathrm{2}{x}^{\mathrm{2}} +{x}+\mathrm{2}}{\mathrm{18}\left({x}−\mathrm{2}\right)\left({x}+\mathrm{1}\right)^{\mathrm{2}} }−\frac{\mathrm{1}}{\mathrm{9}}\int\frac{{dx}}{\left({x}−\mathrm{2}\right)\left({x}+\mathrm{1}\right)} \\ $$$$ \\ $$$$−\frac{\mathrm{1}}{\mathrm{9}}\int\frac{{dx}}{\left({x}−\mathrm{2}\right)\left({x}+\mathrm{1}\right)}= \\ $$$$=\frac{\mathrm{1}}{\mathrm{27}}\int\frac{{dx}}{{x}+\mathrm{1}}−\frac{\mathrm{1}}{\mathrm{27}}\int\frac{{dx}}{{x}−\mathrm{2}}=\frac{\mathrm{1}}{\mathrm{27}}\mathrm{ln}\:\frac{{x}+\mathrm{1}}{{x}−\mathrm{2}}\:+{C} \\ $$$$ \\ $$$$\underset{\mathrm{3}} {\overset{\infty} {\int}}\frac{{x}}{\left({x}+\mathrm{1}\right)^{\mathrm{3}} \left({x}−\mathrm{2}\right)^{\mathrm{2}} }{dx}=\frac{\mathrm{23}}{\mathrm{288}}−\frac{\mathrm{2}}{\mathrm{27}}\mathrm{ln}\:\mathrm{2} \\ $$
Commented by mathmax by abdo last updated on 22/May/20

$$\mathrm{thank}\:\mathrm{you}\:\mathrm{sir}\:\mathrm{mjs} \\ $$
Answered by mathmax by abdo last updated on 22/May/20
![A =∫_3 ^(+∞) ((xdx)/((x+1)^3 (x−2)^2 )) ⇒A =∫_3 ^(+∞) ((xdx)/((((x+1)/(x−2)))^3 (x−2)^5 )) changement ((x+1)/(x−2)) =t give x+1 =tx−2t ⇒(1−t)x =−2t−1 ⇒x =((−2t−1)/(1−t)) =((2t+1)/(t−1)) and x−2 =((2t+1)/(t−1))−2 =((2t+1−2t+2)/(t−1)) =(3/(t−1)) ,(dx/dt) =((2(t−1)−(2t+1))/((t−1)^2 )) =((−3)/((t−1)^2 )) ⇒ A =∫_4 ^1 ((2t+1)/(t−1)) ×((−3dt)/((t−1)^2 t^3 ((3/(t−1)))^5 )) =3 ∫_1 ^4 (((2t+1)(t−1)^5 )/((t−1)^3 t^3 3^5 )) dt =(1/3^4 ) ∫_1 ^4 (((2t+1)(t−1)^2 )/t^3 ) dt =(1/3^4 ) ∫_1 ^4 (((2t+1)(t^2 −2t +1))/t^3 ) dt =(1/3^4 ) ∫_1 ^4 ((2t^3 −4t^2 +2t +t^2 −2t +1)/t^3 )dt =(1/3^4 ) ∫_1 ^4 ((2t^3 −3t^2 +1)/t^3 )dt =(1/(81)) ∫_1 ^4 (2−(3/t) +(1/t^3 ))dt =(1/(81))[2t−3ln∣t∣ −(1/(2t^2 ))]_1 ^4 =(1/(81))(8−6ln2 −(1/(32)) −2 +(1/2)) =(1/(81))(((13)/2) −(1/(32))−6ln(2))](https://www.tinkutara.com/question/Q95045.png)
$$\mathrm{A}\:=\int_{\mathrm{3}} ^{+\infty} \:\frac{\mathrm{xdx}}{\left(\mathrm{x}+\mathrm{1}\right)^{\mathrm{3}} \left(\mathrm{x}−\mathrm{2}\right)^{\mathrm{2}} }\:\Rightarrow\mathrm{A}\:=\int_{\mathrm{3}} ^{+\infty} \:\frac{\mathrm{xdx}}{\left(\frac{\mathrm{x}+\mathrm{1}}{{x}−\mathrm{2}}\right)^{\mathrm{3}} \left({x}−\mathrm{2}\right)^{\mathrm{5}} } \\ $$$${changement}\:\frac{{x}+\mathrm{1}}{{x}−\mathrm{2}}\:={t}\:{give}\:{x}+\mathrm{1}\:={tx}−\mathrm{2}{t}\:\Rightarrow\left(\mathrm{1}−\mathrm{t}\right)\mathrm{x}\:=−\mathrm{2t}−\mathrm{1} \\ $$$$\Rightarrow\mathrm{x}\:=\frac{−\mathrm{2t}−\mathrm{1}}{\mathrm{1}−\mathrm{t}}\:=\frac{\mathrm{2t}+\mathrm{1}}{\mathrm{t}−\mathrm{1}}\:\mathrm{and}\:\mathrm{x}−\mathrm{2}\:=\frac{\mathrm{2t}+\mathrm{1}}{\mathrm{t}−\mathrm{1}}−\mathrm{2}\:=\frac{\mathrm{2t}+\mathrm{1}−\mathrm{2t}+\mathrm{2}}{\mathrm{t}−\mathrm{1}} \\ $$$$=\frac{\mathrm{3}}{\mathrm{t}−\mathrm{1}}\:\:\:,\frac{\mathrm{dx}}{\mathrm{dt}}\:=\frac{\mathrm{2}\left(\mathrm{t}−\mathrm{1}\right)−\left(\mathrm{2t}+\mathrm{1}\right)}{\left(\mathrm{t}−\mathrm{1}\right)^{\mathrm{2}} }\:=\frac{−\mathrm{3}}{\left(\mathrm{t}−\mathrm{1}\right)^{\mathrm{2}} }\:\Rightarrow \\ $$$$\mathrm{A}\:=\int_{\mathrm{4}} ^{\mathrm{1}} \:\frac{\mathrm{2t}+\mathrm{1}}{\mathrm{t}−\mathrm{1}}\:×\frac{−\mathrm{3dt}}{\left(\mathrm{t}−\mathrm{1}\right)^{\mathrm{2}} \mathrm{t}^{\mathrm{3}} \left(\frac{\mathrm{3}}{\mathrm{t}−\mathrm{1}}\right)^{\mathrm{5}} }\:=\mathrm{3}\:\int_{\mathrm{1}} ^{\mathrm{4}} \:\frac{\left(\mathrm{2t}+\mathrm{1}\right)\left(\mathrm{t}−\mathrm{1}\right)^{\mathrm{5}} }{\left(\mathrm{t}−\mathrm{1}\right)^{\mathrm{3}} \mathrm{t}^{\mathrm{3}} \:\mathrm{3}^{\mathrm{5}} }\:\mathrm{dt} \\ $$$$=\frac{\mathrm{1}}{\mathrm{3}^{\mathrm{4}} }\:\int_{\mathrm{1}} ^{\mathrm{4}} \:\frac{\left(\mathrm{2t}+\mathrm{1}\right)\left(\mathrm{t}−\mathrm{1}\right)^{\mathrm{2}} }{\mathrm{t}^{\mathrm{3}} }\:\mathrm{dt} \\ $$$$=\frac{\mathrm{1}}{\mathrm{3}^{\mathrm{4}} }\:\int_{\mathrm{1}} ^{\mathrm{4}} \:\:\frac{\left(\mathrm{2t}+\mathrm{1}\right)\left(\mathrm{t}^{\mathrm{2}} −\mathrm{2t}\:+\mathrm{1}\right)}{\mathrm{t}^{\mathrm{3}} }\:\mathrm{dt} \\ $$$$=\frac{\mathrm{1}}{\mathrm{3}^{\mathrm{4}} }\:\int_{\mathrm{1}} ^{\mathrm{4}} \:\frac{\mathrm{2t}^{\mathrm{3}} −\mathrm{4t}^{\mathrm{2}} +\mathrm{2t}\:+\mathrm{t}^{\mathrm{2}} −\mathrm{2t}\:+\mathrm{1}}{\mathrm{t}^{\mathrm{3}} }\mathrm{dt} \\ $$$$=\frac{\mathrm{1}}{\mathrm{3}^{\mathrm{4}} }\:\int_{\mathrm{1}} ^{\mathrm{4}} \:\frac{\mathrm{2t}^{\mathrm{3}} −\mathrm{3t}^{\mathrm{2}} +\mathrm{1}}{\mathrm{t}^{\mathrm{3}} }\mathrm{dt} \\ $$$$=\frac{\mathrm{1}}{\mathrm{81}}\:\int_{\mathrm{1}} ^{\mathrm{4}} \left(\mathrm{2}−\frac{\mathrm{3}}{\mathrm{t}}\:+\frac{\mathrm{1}}{\mathrm{t}^{\mathrm{3}} }\right)\mathrm{dt}\:\:=\frac{\mathrm{1}}{\mathrm{81}}\left[\mathrm{2t}−\mathrm{3ln}\mid\mathrm{t}\mid\:−\frac{\mathrm{1}}{\mathrm{2t}^{\mathrm{2}} }\right]_{\mathrm{1}} ^{\mathrm{4}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{81}}\left(\mathrm{8}−\mathrm{6ln2}\:−\frac{\mathrm{1}}{\mathrm{32}}\:−\mathrm{2}\:+\frac{\mathrm{1}}{\mathrm{2}}\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{81}}\left(\frac{\mathrm{13}}{\mathrm{2}}\:−\frac{\mathrm{1}}{\mathrm{32}}−\mathrm{6ln}\left(\mathrm{2}\right)\right) \\ $$
