Question Number 82435 by mathmax by abdo last updated on 21/Feb/20
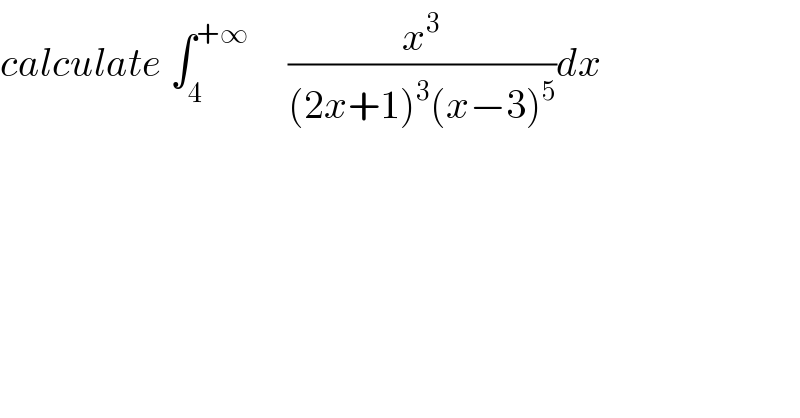
$${calculate}\:\int_{\mathrm{4}} ^{+\infty} \:\:\:\:\:\frac{{x}^{\mathrm{3}} }{\left(\mathrm{2}{x}+\mathrm{1}\right)^{\mathrm{3}} \left({x}−\mathrm{3}\right)^{\mathrm{5}} }{dx} \\ $$
Commented by abdomathmax last updated on 24/Feb/20
![A =∫_4 ^(+∞) (x^3 /((2x+1)^3 (x−3)^5 ))dx ⇒ A =∫_4 ^(+∞) (x^3 /((((2x+1)/(x−3)))^3 (x−3)^8 ))dx changement ((2x+1)/(x−3)) =t give 2x+1=tx−3t ⇒(2−t)x=−3t−1 ⇒ x=((3t+1)/(t−2)) ⇒dx =((3(t−2)−(3t+1))/((t−2)^2 ))=((3t−6−3t−1)/((t−2)^2 )) =((−7)/((t−2)^2 )) and x−3=((3t+1)/(t−2))−3=((3t+1−3t+6)/(t−2)) =(7/(t−2)) ⇒ A =∫_9 ^2 (((((3t+1)/(t−2)))^3 )/(t^3 ((7/(t−2)))^8 ))×(((−7))/((t−2)^2 ))dt =(1/7^7 ) ∫_2 ^9 (((3t+1)^3 )/((t−2)^3 t^3 (t−2)^(−8) (t−2)^2 ))dt =−(1/7^7 )∫_9 ^(+∞) (((3t+1)^3 )/t^3 )(t−2)^3 dt =(1/7^7 ) ∫_2 ^9 (({(3t+1)(t−2)}^3 )/t^3 )dt =(1/7^7 )∫_2 ^9 (((3t^2 −6t+t−2)^3 )/t^3 )dt 7^7 I =∫_2 ^9 (((3t^2 −5t−2)^3 )/t^3 )dt we have (3t^2 −5t−2)^3 =(3t^2 −5t )^3 −3(3t^2 −5t)×2 +3(3t^2 −5t)2^2 −2^3 =t^3 (3t−5)^3 −18t^2 +30t +36t^2 −60t −8 =t^3 ( (3t)^3 −3(3t)^2 ×5 +3(3t)5^2 −5^3 ) +18t^2 −30t −8 =t^3 {27t^3 −15.9t^2 +9.25t −125}+18t^2 −30t−8 =27t^6 −15.9 t^5 +9.25t^4 −125t^3 +18t^2 −30t −8 ⇒ 7^7 I =∫_2 ^9 (27t^3 −15.9 t^2 +9.25t −125+((18)/t)−((30)/t^2 )−(8/t^3 ))dt I=(1/7^7 )[((27)/4)t^4 −((15.9)/3)t^3 +((9.25)/2)t^2 −125t +18ln∣t∣+((30)/t)+(8/(2t^2 ))]_2 ^9](https://www.tinkutara.com/question/Q82801.png)
$${A}\:=\int_{\mathrm{4}} ^{+\infty} \:\frac{{x}^{\mathrm{3}} }{\left(\mathrm{2}{x}+\mathrm{1}\right)^{\mathrm{3}} \left({x}−\mathrm{3}\right)^{\mathrm{5}} }{dx}\:\Rightarrow \\ $$$${A}\:=\int_{\mathrm{4}} ^{+\infty} \:\frac{{x}^{\mathrm{3}} }{\left(\frac{\mathrm{2}{x}+\mathrm{1}}{{x}−\mathrm{3}}\right)^{\mathrm{3}} \left({x}−\mathrm{3}\right)^{\mathrm{8}} }{dx}\:{changement} \\ $$$$\frac{\mathrm{2}{x}+\mathrm{1}}{{x}−\mathrm{3}}\:={t}\:{give}\:\mathrm{2}{x}+\mathrm{1}={tx}−\mathrm{3}{t}\:\Rightarrow\left(\mathrm{2}−{t}\right){x}=−\mathrm{3}{t}−\mathrm{1}\:\Rightarrow \\ $$$${x}=\frac{\mathrm{3}{t}+\mathrm{1}}{{t}−\mathrm{2}}\:\Rightarrow{dx}\:=\frac{\mathrm{3}\left({t}−\mathrm{2}\right)−\left(\mathrm{3}{t}+\mathrm{1}\right)}{\left({t}−\mathrm{2}\right)^{\mathrm{2}} }=\frac{\mathrm{3}{t}−\mathrm{6}−\mathrm{3}{t}−\mathrm{1}}{\left({t}−\mathrm{2}\right)^{\mathrm{2}} } \\ $$$$=\frac{−\mathrm{7}}{\left({t}−\mathrm{2}\right)^{\mathrm{2}} }\:{and}\:{x}−\mathrm{3}=\frac{\mathrm{3}{t}+\mathrm{1}}{{t}−\mathrm{2}}−\mathrm{3}=\frac{\mathrm{3}{t}+\mathrm{1}−\mathrm{3}{t}+\mathrm{6}}{{t}−\mathrm{2}} \\ $$$$=\frac{\mathrm{7}}{{t}−\mathrm{2}}\:\Rightarrow \\ $$$${A}\:=\int_{\mathrm{9}} ^{\mathrm{2}} \:\:\:\frac{\left(\frac{\mathrm{3}{t}+\mathrm{1}}{{t}−\mathrm{2}}\right)^{\mathrm{3}} }{{t}^{\mathrm{3}} \left(\frac{\mathrm{7}}{{t}−\mathrm{2}}\right)^{\mathrm{8}} }×\frac{\left(−\mathrm{7}\right)}{\left({t}−\mathrm{2}\right)^{\mathrm{2}} }{dt} \\ $$$$=\frac{\mathrm{1}}{\mathrm{7}^{\mathrm{7}} }\:\int_{\mathrm{2}} ^{\mathrm{9}} \:\:\frac{\left(\mathrm{3}{t}+\mathrm{1}\right)^{\mathrm{3}} }{\left({t}−\mathrm{2}\right)^{\mathrm{3}} {t}^{\mathrm{3}} \left({t}−\mathrm{2}\right)^{−\mathrm{8}} \left({t}−\mathrm{2}\right)^{\mathrm{2}} }{dt} \\ $$$$=−\frac{\mathrm{1}}{\mathrm{7}^{\mathrm{7}} }\int_{\mathrm{9}} ^{+\infty} \:\:\frac{\left(\mathrm{3}{t}+\mathrm{1}\right)^{\mathrm{3}} }{{t}^{\mathrm{3}} }\left({t}−\mathrm{2}\right)^{\mathrm{3}} \:{dt} \\ $$$$=\frac{\mathrm{1}}{\mathrm{7}^{\mathrm{7}} }\:\int_{\mathrm{2}} ^{\mathrm{9}} \:\:\frac{\left\{\left(\mathrm{3}{t}+\mathrm{1}\right)\left({t}−\mathrm{2}\right)\right\}^{\mathrm{3}} }{{t}^{\mathrm{3}} }{dt} \\ $$$$=\frac{\mathrm{1}}{\mathrm{7}^{\mathrm{7}} }\int_{\mathrm{2}} ^{\mathrm{9}} \:\:\frac{\left(\mathrm{3}{t}^{\mathrm{2}} −\mathrm{6}{t}+{t}−\mathrm{2}\right)^{\mathrm{3}} }{{t}^{\mathrm{3}} }{dt} \\ $$$$\mathrm{7}^{\mathrm{7}} \:{I}\:=\int_{\mathrm{2}} ^{\mathrm{9}} \:\frac{\left(\mathrm{3}{t}^{\mathrm{2}} −\mathrm{5}{t}−\mathrm{2}\right)^{\mathrm{3}} }{{t}^{\mathrm{3}} }{dt} \\ $$$${we}\:{have}\:\left(\mathrm{3}{t}^{\mathrm{2}} −\mathrm{5}{t}−\mathrm{2}\right)^{\mathrm{3}} =\left(\mathrm{3}{t}^{\mathrm{2}} −\mathrm{5}{t}\:\right)^{\mathrm{3}} −\mathrm{3}\left(\mathrm{3}{t}^{\mathrm{2}} −\mathrm{5}{t}\right)×\mathrm{2} \\ $$$$+\mathrm{3}\left(\mathrm{3}{t}^{\mathrm{2}} −\mathrm{5}{t}\right)\mathrm{2}^{\mathrm{2}} −\mathrm{2}^{\mathrm{3}} \\ $$$$={t}^{\mathrm{3}} \left(\mathrm{3}{t}−\mathrm{5}\right)^{\mathrm{3}} −\mathrm{18}{t}^{\mathrm{2}} +\mathrm{30}{t}\:+\mathrm{36}{t}^{\mathrm{2}} −\mathrm{60}{t}\:−\mathrm{8} \\ $$$$={t}^{\mathrm{3}} \left(\:\left(\mathrm{3}{t}\right)^{\mathrm{3}} −\mathrm{3}\left(\mathrm{3}{t}\right)^{\mathrm{2}} ×\mathrm{5}\:+\mathrm{3}\left(\mathrm{3}{t}\right)\mathrm{5}^{\mathrm{2}} −\mathrm{5}^{\mathrm{3}} \right) \\ $$$$+\mathrm{18}{t}^{\mathrm{2}} −\mathrm{30}{t}\:−\mathrm{8} \\ $$$$={t}^{\mathrm{3}} \left\{\mathrm{27}{t}^{\mathrm{3}} −\mathrm{15}.\mathrm{9}{t}^{\mathrm{2}} +\mathrm{9}.\mathrm{25}{t}\:−\mathrm{125}\right\}+\mathrm{18}{t}^{\mathrm{2}} −\mathrm{30}{t}−\mathrm{8} \\ $$$$=\mathrm{27}{t}^{\mathrm{6}} −\mathrm{15}.\mathrm{9}\:{t}^{\mathrm{5}} +\mathrm{9}.\mathrm{25}{t}^{\mathrm{4}} −\mathrm{125}{t}^{\mathrm{3}} \:+\mathrm{18}{t}^{\mathrm{2}} −\mathrm{30}{t}\:−\mathrm{8}\:\Rightarrow \\ $$$$\mathrm{7}^{\mathrm{7}} \:{I}\:=\int_{\mathrm{2}} ^{\mathrm{9}} \left(\mathrm{27}{t}^{\mathrm{3}} −\mathrm{15}.\mathrm{9}\:{t}^{\mathrm{2}} \:+\mathrm{9}.\mathrm{25}{t}\:−\mathrm{125}+\frac{\mathrm{18}}{{t}}−\frac{\mathrm{30}}{{t}^{\mathrm{2}} }−\frac{\mathrm{8}}{{t}^{\mathrm{3}} }\right){dt} \\ $$$${I}=\frac{\mathrm{1}}{\mathrm{7}^{\mathrm{7}} }\left[\frac{\mathrm{27}}{\mathrm{4}}{t}^{\mathrm{4}} −\frac{\mathrm{15}.\mathrm{9}}{\mathrm{3}}{t}^{\mathrm{3}} \:+\frac{\mathrm{9}.\mathrm{25}}{\mathrm{2}}{t}^{\mathrm{2}} −\mathrm{125}{t}\:+\mathrm{18}{ln}\mid{t}\mid+\frac{\mathrm{30}}{{t}}+\frac{\mathrm{8}}{\mathrm{2}{t}^{\mathrm{2}} }\right]_{\mathrm{2}} ^{\mathrm{9}} \\ $$$$ \\ $$
