Question Number 48255 by Abdo msup. last updated on 21/Nov/18
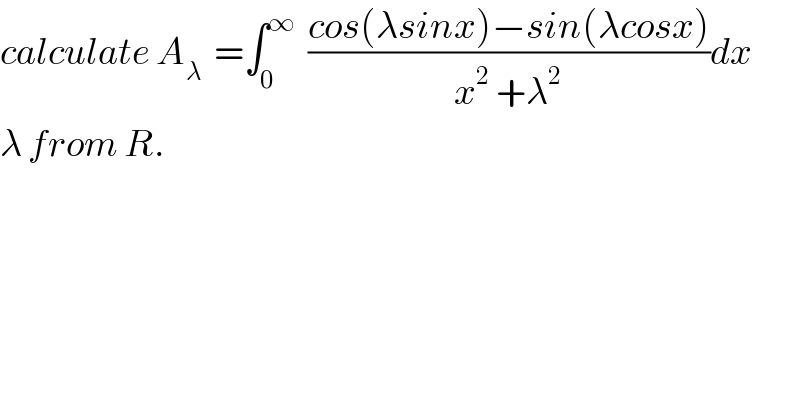
$${calculate}\:{A}_{\lambda} \:\:=\int_{\mathrm{0}} ^{\infty} \:\:\frac{{cos}\left(\lambda{sinx}\right)−{sin}\left(\lambda{cosx}\right)}{{x}^{\mathrm{2}} \:+\lambda^{\mathrm{2}} }{dx} \\ $$$$\lambda\:{from}\:{R}. \\ $$
Commented by Abdo msup. last updated on 23/Nov/18
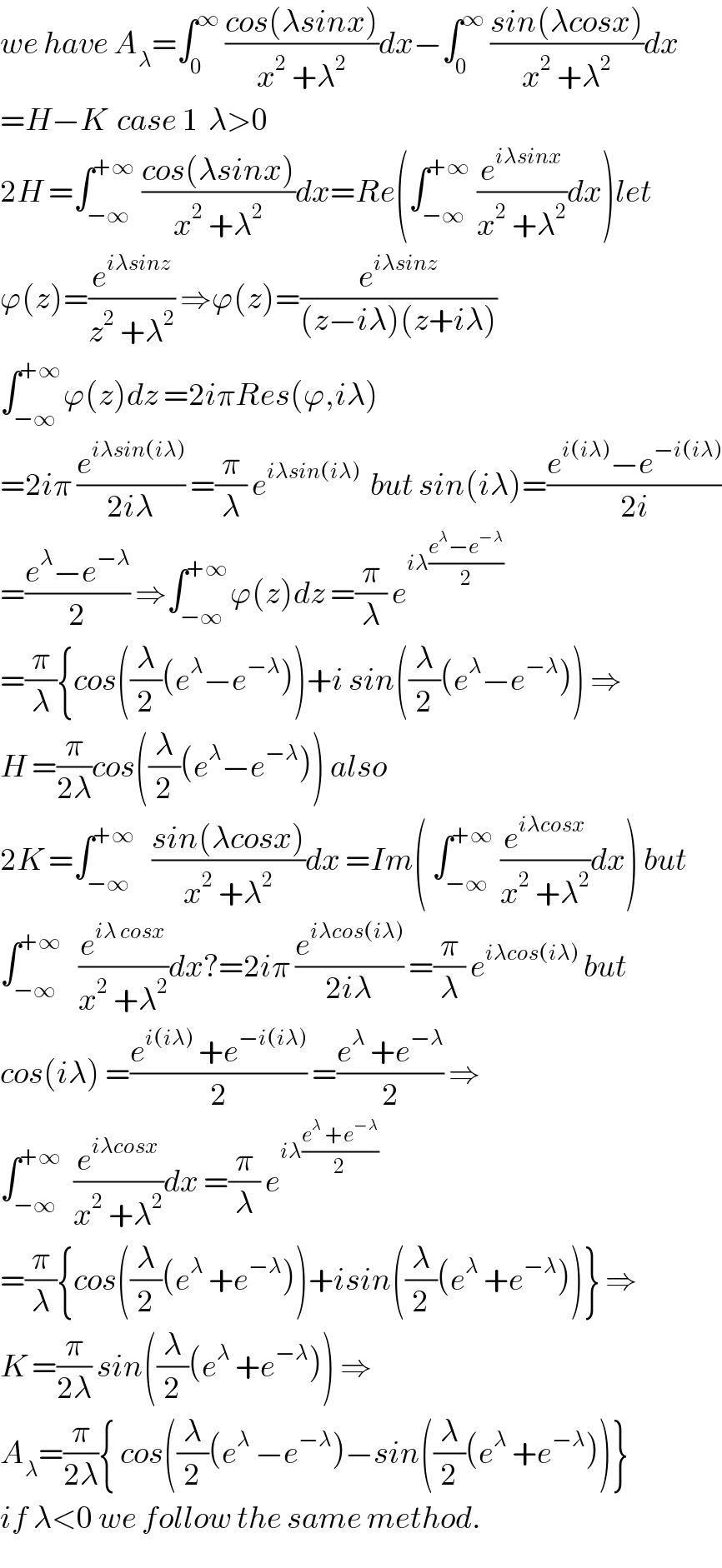
$${we}\:{have}\:{A}_{\lambda} =\int_{\mathrm{0}} ^{\infty} \:\frac{{cos}\left(\lambda{sinx}\right)}{{x}^{\mathrm{2}} \:+\lambda^{\mathrm{2}} }{dx}−\int_{\mathrm{0}} ^{\infty} \:\frac{{sin}\left(\lambda{cosx}\right)}{{x}^{\mathrm{2}} \:+\lambda^{\mathrm{2}} }{dx} \\ $$$$={H}−{K}\:\:{case}\:\mathrm{1}\:\:\lambda>\mathrm{0} \\ $$$$\mathrm{2}{H}\:=\int_{−\infty} ^{+\infty} \:\frac{{cos}\left(\lambda{sinx}\right)}{{x}^{\mathrm{2}} \:+\lambda^{\mathrm{2}} }{dx}={Re}\left(\int_{−\infty} ^{+\infty} \:\frac{{e}^{{i}\lambda{sinx}} }{{x}^{\mathrm{2}} \:+\lambda^{\mathrm{2}} }{dx}\right){let} \\ $$$$\varphi\left({z}\right)=\frac{{e}^{{i}\lambda{sinz}} }{{z}^{\mathrm{2}} \:+\lambda^{\mathrm{2}} }\:\Rightarrow\varphi\left({z}\right)=\frac{{e}^{{i}\lambda{sinz}} }{\left({z}−{i}\lambda\right)\left({z}+{i}\lambda\right)} \\ $$$$\int_{−\infty} ^{+\infty} \varphi\left({z}\right){dz}\:=\mathrm{2}{i}\pi{Res}\left(\varphi,{i}\lambda\right) \\ $$$$=\mathrm{2}{i}\pi\:\frac{{e}^{{i}\lambda{sin}\left({i}\lambda\right)} }{\mathrm{2}{i}\lambda}\:=\frac{\pi}{\lambda}\:{e}^{{i}\lambda{sin}\left({i}\lambda\right)} \:\:{but}\:{sin}\left({i}\lambda\right)=\frac{{e}^{{i}\left({i}\lambda\right)} −{e}^{−{i}\left({i}\lambda\right)} }{\mathrm{2}{i}} \\ $$$$=\frac{{e}^{\lambda} −{e}^{−\lambda} }{\mathrm{2}}\:\Rightarrow\int_{−\infty} ^{+\infty} \varphi\left({z}\right){dz}\:=\frac{\pi}{\lambda}\:{e}^{{i}\lambda\frac{{e}^{\lambda} −{e}^{−\lambda} }{\mathrm{2}}} \\ $$$$=\frac{\pi}{\lambda}\left\{{cos}\left(\frac{\lambda}{\mathrm{2}}\left({e}^{\lambda} −{e}^{−\lambda} \right)\right)+{i}\:{sin}\left(\frac{\lambda}{\mathrm{2}}\left({e}^{\lambda} −{e}^{−\lambda} \right)\right)\:\Rightarrow\right. \\ $$$${H}\:=\frac{\pi}{\mathrm{2}\lambda}{cos}\left(\frac{\lambda}{\mathrm{2}}\left({e}^{\lambda} −{e}^{−\lambda} \right)\right)\:{also} \\ $$$$\mathrm{2}{K}\:=\int_{−\infty} ^{+\infty} \:\:\:\frac{{sin}\left(\lambda{cosx}\right)}{{x}^{\mathrm{2}} \:+\lambda^{\mathrm{2}} }{dx}\:={Im}\left(\:\int_{−\infty} ^{+\infty} \:\frac{{e}^{{i}\lambda{cosx}} }{{x}^{\mathrm{2}} \:+\lambda^{\mathrm{2}} }{dx}\right)\:{but} \\ $$$$\int_{−\infty} ^{+\infty} \:\:\:\frac{{e}^{{i}\lambda\:{cosx}} }{{x}^{\mathrm{2}} \:+\lambda^{\mathrm{2}} }{dx}?=\mathrm{2}{i}\pi\:\frac{{e}^{{i}\lambda{cos}\left({i}\lambda\right)} }{\mathrm{2}{i}\lambda}\:=\frac{\pi}{\lambda}\:{e}^{{i}\lambda{cos}\left({i}\lambda\right)} \:{but} \\ $$$${cos}\left({i}\lambda\right)\:=\frac{{e}^{{i}\left({i}\lambda\right)} \:+{e}^{−{i}\left({i}\lambda\right)} }{\mathrm{2}}\:=\frac{{e}^{\lambda} \:+{e}^{−\lambda} }{\mathrm{2}}\:\Rightarrow \\ $$$$\int_{−\infty} ^{+\infty} \:\:\frac{{e}^{{i}\lambda{cosx}} }{{x}^{\mathrm{2}} \:+\lambda^{\mathrm{2}} }{dx}\:=\frac{\pi}{\lambda}\:{e}^{{i}\lambda\frac{{e}^{\lambda} \:+{e}^{−\lambda} }{\mathrm{2}}} \\ $$$$=\frac{\pi}{\lambda}\left\{{cos}\left(\frac{\lambda}{\mathrm{2}}\left({e}^{\lambda} \:+{e}^{−\lambda} \right)\right)+{isin}\left(\frac{\lambda}{\mathrm{2}}\left({e}^{\lambda} \:+{e}^{−\lambda} \right)\right)\right\}\:\Rightarrow \\ $$$${K}\:=\frac{\pi}{\mathrm{2}\lambda}\:{sin}\left(\frac{\lambda}{\mathrm{2}}\left({e}^{\lambda} \:+{e}^{−\lambda} \right)\right)\:\Rightarrow \\ $$$${A}_{\lambda} =\frac{\pi}{\mathrm{2}\lambda}\left\{\:{cos}\left(\frac{\lambda}{\mathrm{2}}\left({e}^{\lambda} \:−{e}^{−\lambda} \right)−{sin}\left(\frac{\lambda}{\mathrm{2}}\left({e}^{\lambda} \:+{e}^{−\lambda} \right)\right)\right\}\right. \\ $$$${if}\:\lambda<\mathrm{0}\:{we}\:{follow}\:{the}\:{same}\:{method}. \\ $$
