Menu Close

calculate-A-0-pi-4-cos-8-xdx-and-B-0-pi-4-sin-8-xdx-2-calculate-A-B-and-A-B-3-calculate-A-2-B-2-

Tinku Tara 0 Comments
Pin




Question Number 41677 by math khazana by abdo last updated on 11/Aug/18
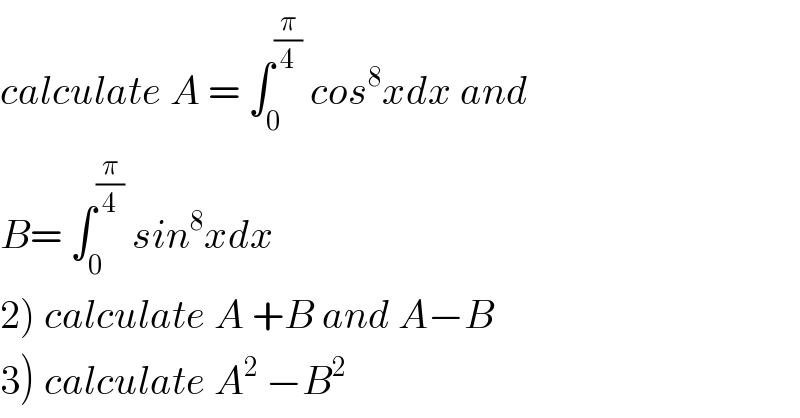
calculate A = ∫_0 ^(π/4) cos^8 xdx and B= ∫_0 ^(π/4) sin^8 xdx 2) calculate A +B and A−B 3) calculate A^2 −B^2
$${calculate}\:{A}\:=\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \:{cos}^{\mathrm{8}} {xdx}\:{and}\: \\ $$$${B}=\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \:{sin}^{\mathrm{8}} {xdx} \\ $$$$\left.\mathrm{2}\right)\:{calculate}\:{A}\:+{B}\:{and}\:{A}−{B} \\ $$$$\left.\mathrm{3}\right)\:{calculate}\:{A}^{\mathrm{2}} \:−{B}^{\mathrm{2}} \\ $$
Commented by math khazana by abdo last updated on 12/Aug/18
let A_n = ∫_0 ^(π/4) cos^(2n) xdx we haveA =A_4 A_(n+1) = ∫_0 ^(π/4) cos^(2n) (1−sin^2 x)dx =A_n −∫_0 ^(π/4) sin^2 x cos^(2n) xdx by parts ∫_0 ^(π/4) sinx(−sinx)cos^(2n) x dx = [(1/(2n+1))sinxcos^(2n+1) x ]_0 ^(π/4) −∫_0 ^(π/4) (1/(2n+1)) cos^(2n+2) xdx =(1/(2n+1))( (1/( (√2))))^(2n+2) −(1/(2n+1)) A_(n+1) ⇒ (1+(1/(2n+1)))A_(n+1) =A_n +(1/((2n+1)2^(n+1) )) ⇒ ((2n+2)/(2n+1)) A_(n+1) = A_n +(1/((2n+1)2^(n+1) )) ⇒ A_(n+1) =((2n+1)/(2n+2)) A_n + (1/((2n+2)2^(n+1) )) ⇒ A_4 =(7/8) A_3 + (1/(8.2^4 )) A_3 =(5/6) A_2 + (1/(6.2^3 )) A_2 = (3/4) A_1 + (1/(4.2^2 )) A_1 =(1/2) A_0 +(1/4) ⇒ A_4 =(7/8){(5/6) A_2 +(1/(6.2^3 ))} +(1/(8.2^4 )) = ((35)/(48)) A_2 +(7/(48.2^3 )) +(1/(8.2^4 )) =((35)/(48)){ (3/4) A_1 +(1/(4.2^2 ))} +(7/(48.2^3 )) +(1/(8.2^4 )) = ((105)/(192)) A_1 + ((35)/(192.2^2 )) +(7/(48.2^3 )) +(1/(8.2^4 )) =((105)/(192)){(1/2)A_0 +(1/4)} +((35)/(192.2^2 )) +(7/(48.2^3 )) +(1/(8.2^4 )) =((105)/(192)){ (π/8) +(1/4)} +((35)/(192.2^2 )) +(7/(48.2^3 )) +(1/(8.2^4 )) =A
$${let}\:\:{A}_{{n}} =\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \:{cos}^{\mathrm{2}{n}} {xdx}\:\:\:{we}\:{haveA}\:={A}_{\mathrm{4}} \\ $$$${A}_{{n}+\mathrm{1}} =\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \:\:{cos}^{\mathrm{2}{n}} \left(\mathrm{1}−{sin}^{\mathrm{2}} {x}\right){dx} \\ $$$$={A}_{{n}} \:−\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \:{sin}^{\mathrm{2}} {x}\:{cos}^{\mathrm{2}{n}} {xdx}\:\:{by}\:{parts} \\ $$$$\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \:{sinx}\left(−{sinx}\right){cos}^{\mathrm{2}{n}} {x}\:{dx} \\ $$$$=\:\left[\frac{\mathrm{1}}{\mathrm{2}{n}+\mathrm{1}}{sinxcos}^{\mathrm{2}{n}+\mathrm{1}} {x}\:\right]_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \:−\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \:\frac{\mathrm{1}}{\mathrm{2}{n}+\mathrm{1}}\:{cos}^{\mathrm{2}{n}+\mathrm{2}} {xdx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}{n}+\mathrm{1}}\left(\:\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\right)^{\mathrm{2}{n}+\mathrm{2}} \:−\frac{\mathrm{1}}{\mathrm{2}{n}+\mathrm{1}}\:{A}_{{n}+\mathrm{1}} \:\Rightarrow \\ $$$$\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}{n}+\mathrm{1}}\right){A}_{{n}+\mathrm{1}} ={A}_{{n}} \:\:\:+\frac{\mathrm{1}}{\left(\mathrm{2}{n}+\mathrm{1}\right)\mathrm{2}^{{n}+\mathrm{1}} }\:\Rightarrow \\ $$$$\frac{\mathrm{2}{n}+\mathrm{2}}{\mathrm{2}{n}+\mathrm{1}}\:{A}_{{n}+\mathrm{1}} =\:{A}_{{n}} \:+\frac{\mathrm{1}}{\left(\mathrm{2}{n}+\mathrm{1}\right)\mathrm{2}^{{n}+\mathrm{1}} }\:\Rightarrow \\ $$$${A}_{{n}+\mathrm{1}} =\frac{\mathrm{2}{n}+\mathrm{1}}{\mathrm{2}{n}+\mathrm{2}}\:{A}_{{n}} \:+\:\frac{\mathrm{1}}{\left(\mathrm{2}{n}+\mathrm{2}\right)\mathrm{2}^{{n}+\mathrm{1}} }\:\Rightarrow \\ $$$${A}_{\mathrm{4}} =\frac{\mathrm{7}}{\mathrm{8}}\:{A}_{\mathrm{3}} \:+\:\frac{\mathrm{1}}{\mathrm{8}.\mathrm{2}^{\mathrm{4}} } \\ $$$${A}_{\mathrm{3}} =\frac{\mathrm{5}}{\mathrm{6}}\:{A}_{\mathrm{2}} \:+\:\frac{\mathrm{1}}{\mathrm{6}.\mathrm{2}^{\mathrm{3}} } \\ $$$${A}_{\mathrm{2}} =\:\frac{\mathrm{3}}{\mathrm{4}}\:{A}_{\mathrm{1}} \:+\:\frac{\mathrm{1}}{\mathrm{4}.\mathrm{2}^{\mathrm{2}} } \\ $$$${A}_{\mathrm{1}} =\frac{\mathrm{1}}{\mathrm{2}}\:{A}_{\mathrm{0}} \:+\frac{\mathrm{1}}{\mathrm{4}}\:\Rightarrow \\ $$$${A}_{\mathrm{4}} =\frac{\mathrm{7}}{\mathrm{8}}\left\{\frac{\mathrm{5}}{\mathrm{6}}\:{A}_{\mathrm{2}} \:+\frac{\mathrm{1}}{\mathrm{6}.\mathrm{2}^{\mathrm{3}} }\right\}\:+\frac{\mathrm{1}}{\mathrm{8}.\mathrm{2}^{\mathrm{4}} } \\ $$$$=\:\frac{\mathrm{35}}{\mathrm{48}}\:{A}_{\mathrm{2}} \:\:+\frac{\mathrm{7}}{\mathrm{48}.\mathrm{2}^{\mathrm{3}} }\:+\frac{\mathrm{1}}{\mathrm{8}.\mathrm{2}^{\mathrm{4}} } \\ $$$$=\frac{\mathrm{35}}{\mathrm{48}}\left\{\:\frac{\mathrm{3}}{\mathrm{4}}\:{A}_{\mathrm{1}} +\frac{\mathrm{1}}{\mathrm{4}.\mathrm{2}^{\mathrm{2}} }\right\}\:+\frac{\mathrm{7}}{\mathrm{48}.\mathrm{2}^{\mathrm{3}} }\:+\frac{\mathrm{1}}{\mathrm{8}.\mathrm{2}^{\mathrm{4}} } \\ $$$$=\:\frac{\mathrm{105}}{\mathrm{192}}\:{A}_{\mathrm{1}} \:+\:\frac{\mathrm{35}}{\mathrm{192}.\mathrm{2}^{\mathrm{2}} }\:+\frac{\mathrm{7}}{\mathrm{48}.\mathrm{2}^{\mathrm{3}} }\:+\frac{\mathrm{1}}{\mathrm{8}.\mathrm{2}^{\mathrm{4}} } \\ $$$$=\frac{\mathrm{105}}{\mathrm{192}}\left\{\frac{\mathrm{1}}{\mathrm{2}}{A}_{\mathrm{0}} \:+\frac{\mathrm{1}}{\mathrm{4}}\right\}\:+\frac{\mathrm{35}}{\mathrm{192}.\mathrm{2}^{\mathrm{2}} }\:+\frac{\mathrm{7}}{\mathrm{48}.\mathrm{2}^{\mathrm{3}} }\:+\frac{\mathrm{1}}{\mathrm{8}.\mathrm{2}^{\mathrm{4}} } \\ $$$$=\frac{\mathrm{105}}{\mathrm{192}}\left\{\:\frac{\pi}{\mathrm{8}}\:+\frac{\mathrm{1}}{\mathrm{4}}\right\}\:+\frac{\mathrm{35}}{\mathrm{192}.\mathrm{2}^{\mathrm{2}} }\:+\frac{\mathrm{7}}{\mathrm{48}.\mathrm{2}^{\mathrm{3}} }\:+\frac{\mathrm{1}}{\mathrm{8}.\mathrm{2}^{\mathrm{4}} }\:={A} \\ $$
Commented by math khazana by abdo last updated on 12/Aug/18
let B_n = ∫_0 ^(π/4) sin^(2n) xdx we have B=B_4 B_(n+1) = ∫_0 ^(π/4) sin^(2n) (1−cos^2 x)dx = ∫_0 ^(π/4) sin^(2n) xdx − ∫_0 ^(π/4) cosx (cosx)sin^(2n) xdx by parts ∫_0 ^(π/4) cosx(cosx)sin^(2n) xdx=[(1/(2n+1))cosxsin^(2n+1) x]_0 ^(π/4) − ∫_0 ^(π/4) (−sinx) (1/(2n+1)) sin^(2n+1) xdx = (1/((2n+1)))((1/( (√2))))^(2n+2) +(1/(2n+1)) ∫_0 ^(π/4) sin^(2n+2) xdx = (1/((2n+1)2^(n+1) )) +(1/(2n+1)) B_(n+1) ⇒ B_(n+1) =B_n − (1/((2n+1)2^(n+1) )) −(1/(2n+1)) B_(n+1) ⇒ (1+(1/(2n+1)))B_(n+1) =B_n −(1/((2n+1)2^(n+1) )) ⇒ ((2n+2)/(2n+1)) B_(n+1) =B_n −(1/((2n+1)2^(n+1) )) ⇒ B_(n+1) =((2n+1)/(2n+2)) B_n − (1/((2n+2)2^(n+1) )) ...be continued...
$${let}\:{B}_{{n}} =\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \:{sin}^{\mathrm{2}{n}} {xdx}\:\:{we}\:{have}\:{B}={B}_{\mathrm{4}} \\ $$$${B}_{{n}+\mathrm{1}} =\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \:{sin}^{\mathrm{2}{n}} \left(\mathrm{1}−{cos}^{\mathrm{2}} {x}\right){dx} \\ $$$$=\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \:{sin}^{\mathrm{2}{n}} {xdx}\:−\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \:{cosx}\:\left({cosx}\right){sin}^{\mathrm{2}{n}} {xdx}\:\:{by} \\ $$$${parts}\: \\ $$$$\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \:{cosx}\left({cosx}\right){sin}^{\mathrm{2}{n}} {xdx}=\left[\frac{\mathrm{1}}{\mathrm{2}{n}+\mathrm{1}}{cosxsin}^{\mathrm{2}{n}+\mathrm{1}} {x}\right]_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \\ $$$$−\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \:\left(−{sinx}\right)\:\frac{\mathrm{1}}{\mathrm{2}{n}+\mathrm{1}}\:{sin}^{\mathrm{2}{n}+\mathrm{1}} {xdx} \\ $$$$=\:\:\frac{\mathrm{1}}{\left(\mathrm{2}{n}+\mathrm{1}\right)}\left(\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\right)^{\mathrm{2}{n}+\mathrm{2}} \:\:+\frac{\mathrm{1}}{\mathrm{2}{n}+\mathrm{1}}\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \:{sin}^{\mathrm{2}{n}+\mathrm{2}} {xdx} \\ $$$$=\:\frac{\mathrm{1}}{\left(\mathrm{2}{n}+\mathrm{1}\right)\mathrm{2}^{{n}+\mathrm{1}} }\:\:+\frac{\mathrm{1}}{\mathrm{2}{n}+\mathrm{1}}\:{B}_{{n}+\mathrm{1}} \:\:\Rightarrow \\ $$$${B}_{{n}+\mathrm{1}} ={B}_{{n}} \:−\:\frac{\mathrm{1}}{\left(\mathrm{2}{n}+\mathrm{1}\right)\mathrm{2}^{{n}+\mathrm{1}} }\:−\frac{\mathrm{1}}{\mathrm{2}{n}+\mathrm{1}}\:{B}_{{n}+\mathrm{1}} \:\Rightarrow \\ $$$$\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}{n}+\mathrm{1}}\right){B}_{{n}+\mathrm{1}} ={B}_{{n}} −\frac{\mathrm{1}}{\left(\mathrm{2}{n}+\mathrm{1}\right)\mathrm{2}^{{n}+\mathrm{1}} }\:\Rightarrow \\ $$$$\frac{\mathrm{2}{n}+\mathrm{2}}{\mathrm{2}{n}+\mathrm{1}}\:{B}_{{n}+\mathrm{1}} ={B}_{{n}} −\frac{\mathrm{1}}{\left(\mathrm{2}{n}+\mathrm{1}\right)\mathrm{2}^{{n}+\mathrm{1}} }\:\Rightarrow \\ $$$${B}_{{n}+\mathrm{1}} =\frac{\mathrm{2}{n}+\mathrm{1}}{\mathrm{2}{n}+\mathrm{2}}\:{B}_{{n}} \:−\:\frac{\mathrm{1}}{\left(\mathrm{2}{n}+\mathrm{2}\right)\mathrm{2}^{{n}+\mathrm{1}} }\:\:…{be}\:{continued}… \\ $$
Answered by ajfour last updated on 11/Aug/18
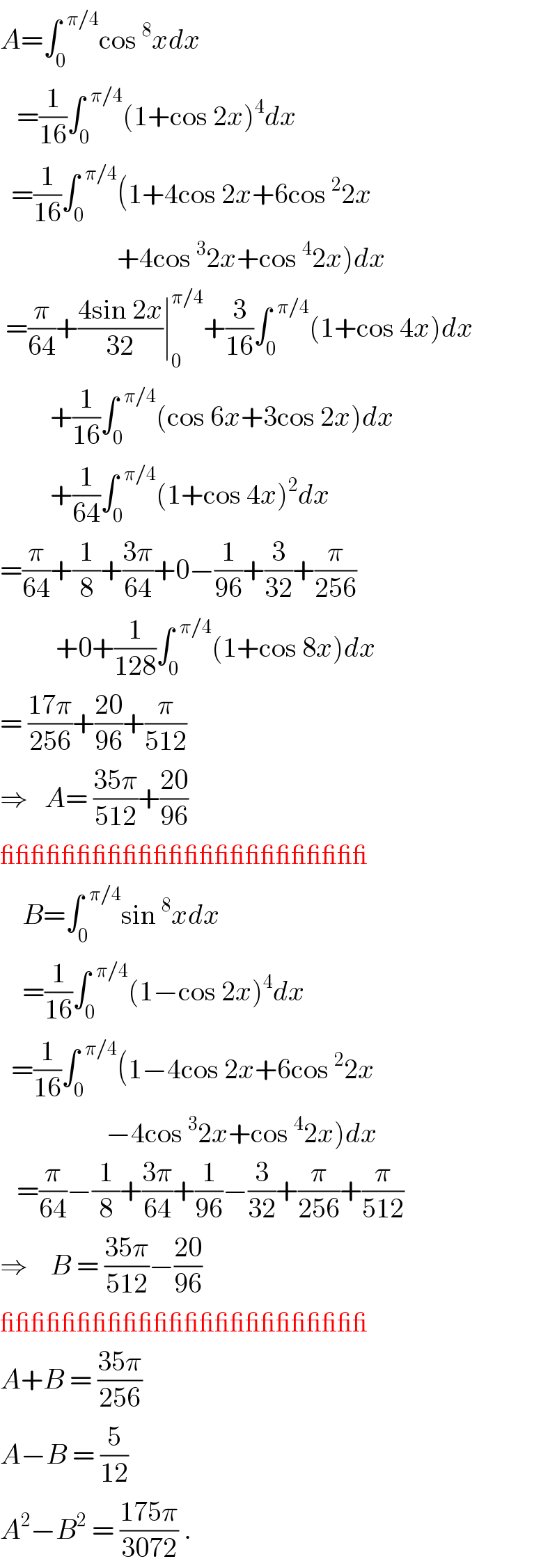
A=∫_0 ^( π/4) cos^8 xdx =(1/(16))∫_0 ^( π/4) (1+cos 2x)^4 dx =(1/(16))∫_0 ^( π/4) (1+4cos 2x+6cos^2 2x +4cos^3 2x+cos^4 2x)dx =(π/(64))+((4sin 2x)/(32))∣_0 ^(π/4) +(3/(16))∫_0 ^( π/4) (1+cos 4x)dx +(1/(16))∫_0 ^( π/4) (cos 6x+3cos 2x)dx +(1/(64))∫_0 ^( π/4) (1+cos 4x)^2 dx =(π/(64))+(1/8)+((3π)/(64))+0−(1/(96))+(3/(32))+(π/(256)) +0+(1/(128))∫_0 ^( π/4) (1+cos 8x)dx = ((17π)/(256))+((20)/(96))+(π/(512)) ⇒ A= ((35π)/(512))+((20)/(96)) ________________________ B=∫_0 ^( π/4) sin^8 xdx =(1/(16))∫_0 ^( π/4) (1−cos 2x)^4 dx =(1/(16))∫_0 ^( π/4) (1−4cos 2x+6cos^2 2x −4cos^3 2x+cos^4 2x)dx =(π/(64))−(1/8)+((3π)/(64))+(1/(96))−(3/(32))+(π/(256))+(π/(512)) ⇒ B = ((35π)/(512))−((20)/(96)) ________________________ A+B = ((35π)/(256)) A−B = (5/(12)) A^2 −B^2 = ((175π)/(3072)) .
$${A}=\int_{\mathrm{0}} ^{\:\:\pi/\mathrm{4}} \mathrm{cos}\:^{\mathrm{8}} {xdx} \\ $$$$\:\:\:=\frac{\mathrm{1}}{\mathrm{16}}\int_{\mathrm{0}} ^{\:\:\pi/\mathrm{4}} \left(\mathrm{1}+\mathrm{cos}\:\mathrm{2}{x}\right)^{\mathrm{4}} {dx} \\ $$$$\:\:=\frac{\mathrm{1}}{\mathrm{16}}\int_{\mathrm{0}} ^{\:\:\pi/\mathrm{4}} \left(\mathrm{1}+\mathrm{4cos}\:\mathrm{2}{x}+\mathrm{6cos}\:^{\mathrm{2}} \mathrm{2}{x}\right. \\ $$$$\left.\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:+\mathrm{4cos}\:^{\mathrm{3}} \mathrm{2}{x}+\mathrm{cos}\:^{\mathrm{4}} \mathrm{2}{x}\right){dx} \\ $$$$\:=\frac{\pi}{\mathrm{64}}+\frac{\mathrm{4sin}\:\mathrm{2}{x}}{\mathrm{32}}\mid_{\mathrm{0}} ^{\pi/\mathrm{4}} +\frac{\mathrm{3}}{\mathrm{16}}\int_{\mathrm{0}} ^{\:\:\pi/\mathrm{4}} \left(\mathrm{1}+\mathrm{cos}\:\mathrm{4}{x}\right){dx} \\ $$$$\:\:\:\:\:\:\:\:\:+\frac{\mathrm{1}}{\mathrm{16}}\int_{\mathrm{0}} ^{\:\:\pi/\mathrm{4}} \left(\mathrm{cos}\:\mathrm{6}{x}+\mathrm{3cos}\:\mathrm{2}{x}\right){dx} \\ $$$$\:\:\:\:\:\:\:\:\:+\frac{\mathrm{1}}{\mathrm{64}}\int_{\mathrm{0}} ^{\:\:\pi/\mathrm{4}} \left(\mathrm{1}+\mathrm{cos}\:\mathrm{4}{x}\right)^{\mathrm{2}} {dx} \\ $$$$=\frac{\pi}{\mathrm{64}}+\frac{\mathrm{1}}{\mathrm{8}}+\frac{\mathrm{3}\pi}{\mathrm{64}}+\mathrm{0}−\frac{\mathrm{1}}{\mathrm{96}}+\frac{\mathrm{3}}{\mathrm{32}}+\frac{\pi}{\mathrm{256}} \\ $$$$\:\:\:\:\:\:\:\:\:\:+\mathrm{0}+\frac{\mathrm{1}}{\mathrm{128}}\int_{\mathrm{0}} ^{\:\:\pi/\mathrm{4}} \left(\mathrm{1}+\mathrm{cos}\:\mathrm{8}{x}\right){dx} \\ $$$$=\:\frac{\mathrm{17}\pi}{\mathrm{256}}+\frac{\mathrm{20}}{\mathrm{96}}+\frac{\pi}{\mathrm{512}}\: \\ $$$$\Rightarrow\:\:\:{A}=\:\frac{\mathrm{35}\pi}{\mathrm{512}}+\frac{\mathrm{20}}{\mathrm{96}} \\ $$$$\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_ \\ $$$$\:\:\:\:{B}=\int_{\mathrm{0}} ^{\:\:\pi/\mathrm{4}} \mathrm{sin}\:^{\mathrm{8}} {xdx} \\ $$$$\:\:\:\:=\frac{\mathrm{1}}{\mathrm{16}}\int_{\mathrm{0}} ^{\:\:\pi/\mathrm{4}} \left(\mathrm{1}−\mathrm{cos}\:\mathrm{2}{x}\right)^{\mathrm{4}} {dx} \\ $$$$\:\:=\frac{\mathrm{1}}{\mathrm{16}}\int_{\mathrm{0}} ^{\:\:\pi/\mathrm{4}} \left(\mathrm{1}−\mathrm{4cos}\:\mathrm{2}{x}+\mathrm{6cos}\:^{\mathrm{2}} \mathrm{2}{x}\right. \\ $$$$\left.\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:−\mathrm{4cos}\:^{\mathrm{3}} \mathrm{2}{x}+\mathrm{cos}\:^{\mathrm{4}} \mathrm{2}{x}\right){dx} \\ $$$$\:\:\:=\frac{\pi}{\mathrm{64}}−\frac{\mathrm{1}}{\mathrm{8}}+\frac{\mathrm{3}\pi}{\mathrm{64}}+\frac{\mathrm{1}}{\mathrm{96}}−\frac{\mathrm{3}}{\mathrm{32}}+\frac{\pi}{\mathrm{256}}+\frac{\pi}{\mathrm{512}} \\ $$$$\Rightarrow\:\:\:\:{B}\:=\:\frac{\mathrm{35}\pi}{\mathrm{512}}−\frac{\mathrm{20}}{\mathrm{96}} \\ $$$$\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_ \\ $$$${A}+{B}\:=\:\frac{\mathrm{35}\pi}{\mathrm{256}} \\ $$$${A}−{B}\:=\:\frac{\mathrm{5}}{\mathrm{12}} \\ $$$${A}^{\mathrm{2}} −{B}^{\mathrm{2}} \:=\:\frac{\mathrm{175}\pi}{\mathrm{3072}}\:. \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 11/Aug/18
method 1 cos^8 x+sin^8 x =(cos^4 x+sin^4 x)^2 −2cos^4 xsin^4 x ={(cos^2 x+sin^2 x)^2 −2cos^2 x.sin^2 x}^2 −(1/8)×(2sinxcosx)^4 ={1−(1/2)(2sinxcosx)^2 }^2 −(1/8)×(sin2x)^4 ={((2−sin^2 2x)/2)}^2 −(1/8)(((1−cos4x)/2))^2 ={((2−((1−cos4x)/2))/2)}^2 −(1/8)(((1−2cos4x+((1+cos8x)/2))/4)) ={((4−1+cos4x)/4)}^2 −(1/8)(((2−4cos4x+1+cos8x)/8)) ={((9+6cos4x+((1+cos8x)/2))/(16))}−(((cos8x−4cos4x+3)/(64))) ={((18+12cos4x+1+cos8x)/(32))}−(((cos8x−4cos4x+3)/(64))) =(((cos8x+12cos4x+19)/(32)))−(((cos8x−4cos4x+3)/(64))) =(((2cos8x+24cos4x+38−cos8x+4cos4x−3)/(64))) =(((cos8x+28cos4x+35)/(64))) so A+B= ∫_0 ^(Π/4) ((cos8x+28cos4x+35)/(64))dx =(1/(64))∣(((sin8x)/8)+((28sin4x)/4)+35x)∣_0 ^(Π/4) =(1/(64))(((sin2Π)/8)+((28sinΠ)/4)+((35×(Π/4))/)) =(1/(64))×((35Π)/4)=((35Π)/(256)) pls check i shall solve it by gamma beta function later
$${method}\:\mathrm{1} \\ $$$${cos}^{\mathrm{8}} {x}+{sin}^{\mathrm{8}} {x} \\ $$$$=\left({cos}^{\mathrm{4}} {x}+{sin}^{\mathrm{4}} {x}\right)^{\mathrm{2}} −\mathrm{2}{cos}^{\mathrm{4}} {xsin}^{\mathrm{4}} {x} \\ $$$$=\left\{\left({cos}^{\mathrm{2}} {x}+{sin}^{\mathrm{2}} {x}\right)^{\mathrm{2}} −\mathrm{2}{cos}^{\mathrm{2}} {x}.{sin}^{\mathrm{2}} {x}\right\}^{\mathrm{2}} −\frac{\mathrm{1}}{\mathrm{8}}×\left(\mathrm{2}{sinxcosx}\right)^{\mathrm{4}} \\ $$$$=\left\{\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{2}{sinxcosx}\right)^{\mathrm{2}} \right\}^{\mathrm{2}} −\frac{\mathrm{1}}{\mathrm{8}}×\left({sin}\mathrm{2}{x}\right)^{\mathrm{4}} \\ $$$$=\left\{\frac{\mathrm{2}−{sin}^{\mathrm{2}} \mathrm{2}{x}}{\mathrm{2}}\right\}^{\mathrm{2}} −\frac{\mathrm{1}}{\mathrm{8}}\left(\frac{\mathrm{1}−{cos}\mathrm{4}{x}}{\mathrm{2}}\right)^{\mathrm{2}} \\ $$$$=\left\{\frac{\mathrm{2}−\frac{\mathrm{1}−{cos}\mathrm{4}{x}}{\mathrm{2}}}{\mathrm{2}}\right\}^{\mathrm{2}} −\frac{\mathrm{1}}{\mathrm{8}}\left(\frac{\mathrm{1}−\mathrm{2}{cos}\mathrm{4}{x}+\frac{\mathrm{1}+{cos}\mathrm{8}{x}}{\mathrm{2}}}{\mathrm{4}}\right) \\ $$$$=\left\{\frac{\mathrm{4}−\mathrm{1}+{cos}\mathrm{4}{x}}{\mathrm{4}}\right\}^{\mathrm{2}} −\frac{\mathrm{1}}{\mathrm{8}}\left(\frac{\mathrm{2}−\mathrm{4}{cos}\mathrm{4}{x}+\mathrm{1}+{cos}\mathrm{8}{x}}{\mathrm{8}}\right) \\ $$$$=\left\{\frac{\mathrm{9}+\mathrm{6}{cos}\mathrm{4}{x}+\frac{\mathrm{1}+{cos}\mathrm{8}{x}}{\mathrm{2}}}{\mathrm{16}}\right\}−\left(\frac{{cos}\mathrm{8}{x}−\mathrm{4}{cos}\mathrm{4}{x}+\mathrm{3}}{\mathrm{64}}\right) \\ $$$$=\left\{\frac{\mathrm{18}+\mathrm{12}{cos}\mathrm{4}{x}+\mathrm{1}+{cos}\mathrm{8}{x}}{\mathrm{32}}\right\}−\left(\frac{{cos}\mathrm{8}{x}−\mathrm{4}{cos}\mathrm{4}{x}+\mathrm{3}}{\mathrm{64}}\right) \\ $$$$=\left(\frac{{cos}\mathrm{8}{x}+\mathrm{12}{cos}\mathrm{4}{x}+\mathrm{19}}{\mathrm{32}}\right)−\left(\frac{{cos}\mathrm{8}{x}−\mathrm{4}{cos}\mathrm{4}{x}+\mathrm{3}}{\mathrm{64}}\right) \\ $$$$=\left(\frac{\mathrm{2}{cos}\mathrm{8}{x}+\mathrm{24}{cos}\mathrm{4}{x}+\mathrm{38}−{cos}\mathrm{8}{x}+\mathrm{4}{cos}\mathrm{4}{x}−\mathrm{3}}{\mathrm{64}}\right) \\ $$$$=\left(\frac{{cos}\mathrm{8}{x}+\mathrm{28}{cos}\mathrm{4}{x}+\mathrm{35}}{\mathrm{64}}\right) \\ $$$${so}\:{A}+{B}= \\ $$$$\int_{\mathrm{0}} ^{\frac{\Pi}{\mathrm{4}}} \frac{{cos}\mathrm{8}{x}+\mathrm{28}{cos}\mathrm{4}{x}+\mathrm{35}}{\mathrm{64}}{dx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{64}}\mid\left(\frac{{sin}\mathrm{8}{x}}{\mathrm{8}}+\frac{\mathrm{28}{sin}\mathrm{4}{x}}{\mathrm{4}}+\mathrm{35}{x}\right)\mid_{\mathrm{0}} ^{\frac{\Pi}{\mathrm{4}}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{64}}\left(\frac{{sin}\mathrm{2}\Pi}{\mathrm{8}}+\frac{\mathrm{28}{sin}\Pi}{\mathrm{4}}+\frac{\mathrm{35}×\frac{\Pi}{\mathrm{4}}}{}\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{64}}×\frac{\mathrm{35}\Pi}{\mathrm{4}}=\frac{\mathrm{35}\Pi}{\mathrm{256}}\:\:{pls}\:{check} \\ $$$${i}\:{shall}\:{solve}\:{it}\:{by}\:{gamma}\:{beta}\:{function}\:{later} \\ $$$$ \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *