Menu Close

calculate-A-0-x-2017-1-x-2019-dx-and-B-0-x-2019-1-x-2021-dx-calculate-the-fraction-A-B-

Tinku Tara 0 Comments
Pin




Question Number 63892 by mathmax by abdo last updated on 10/Jul/19
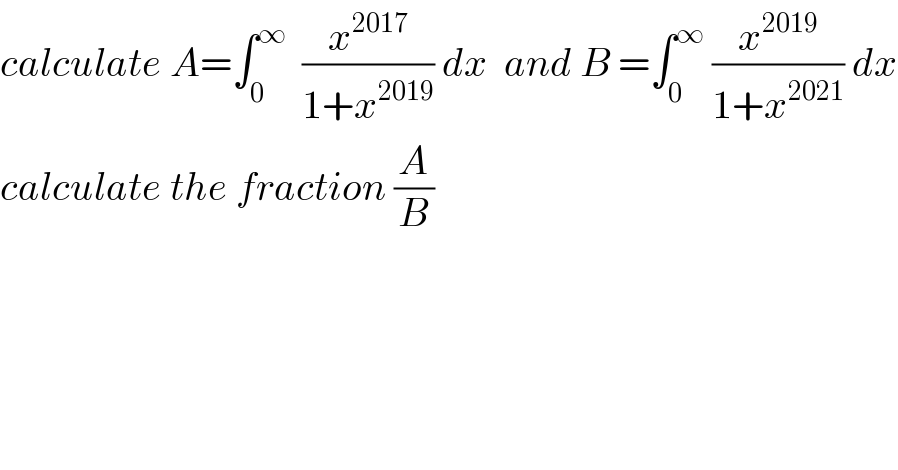
calculate A=∫_0 ^∞ (x^(2017) /(1+x^(2019) )) dx and B =∫_0 ^∞ (x^(2019) /(1+x^(2021) )) dx calculate the fraction (A/B)
$${calculate}\:{A}=\int_{\mathrm{0}} ^{\infty} \:\:\frac{{x}^{\mathrm{2017}} }{\mathrm{1}+{x}^{\mathrm{2019}} }\:{dx}\:\:{and}\:{B}\:=\int_{\mathrm{0}} ^{\infty} \:\frac{{x}^{\mathrm{2019}} }{\mathrm{1}+{x}^{\mathrm{2021}} }\:{dx} \\ $$$${calculate}\:{the}\:{fraction}\:\frac{{A}}{{B}} \\ $$
Commented by Prithwish sen last updated on 11/Jul/19
A′(t) = ∫_0 ^∞ (∂/∂t)[(x^(t−2) /(1+x^t ))]dx = ∫_0 ^∞ (1/x^2 ) (∂/∂t)[1−(1/(1+x^t ))]dx = ∫_0 ^∞ (1/x^2 ) .(1/((1+x^t )^2 ))dx
$$\mathrm{A}'\left(\mathrm{t}\right)\:=\:\int_{\mathrm{0}} ^{\infty} \frac{\partial}{\partial\mathrm{t}}\left[\frac{\mathrm{x}^{\mathrm{t}−\mathrm{2}} }{\mathrm{1}+\mathrm{x}^{\mathrm{t}} }\right]\mathrm{dx}\:=\:\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}} }\:\frac{\partial}{\partial\mathrm{t}}\left[\mathrm{1}−\frac{\mathrm{1}}{\mathrm{1}+\mathrm{x}^{\mathrm{t}} }\right]\mathrm{dx} \\ $$$$=\:\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}} }\:.\frac{\mathrm{1}}{\left(\mathrm{1}+\mathrm{x}^{\mathrm{t}} \right)^{\mathrm{2}} }\mathrm{dx}\: \\ $$
Commented by mathmax by abdo last updated on 12/Jul/19
let f(t) =∫_0 ^∞ (x^(t−2) /(1+x^t )) dt witht>2 changement x^t =u give x =u^(1/t) ⇒f(t) =∫_0 ^∞ (((u^(1/t) )^(t−2) )/(1+u)) (1/t) u^((1/t)−1) du =(1/t)∫_0 ^∞ (u^(((t−2)/t)+(1/t)−1) /(1+u)) du =(1/t)∫_0 ^∞ (u^(((t−1)/t) −1) /(1+u)) du we have t>2 ⇒ (1/t)<(1/2) ⇒−(1/t)>−(1/2) ⇒1−(1/t)>(1/2) ⇒ ((t−1)/t)>(1/2) and ((t−1)/t)=1−(1/t)<1 ⇒ f(t)=(1/t) (π/(sin(π(((t−1)/t))))) =(π/(t sin(π−(π/t)))) =(π/(t sin((π/t)))) ∫_0 ^∞ (x^(2017) /(1+x^(2019) )) =∫_0 ^∞ (x^(2019 −2) /(1+x^(2919) )) =f(2019) =(π/(2019 sin((π/(2019))))) =A B =f(2021) =(π/(2021 sin((π/(2021)))))
$${let}\:{f}\left({t}\right)\:=\int_{\mathrm{0}} ^{\infty} \:\:\frac{{x}^{{t}−\mathrm{2}} }{\mathrm{1}+{x}^{{t}} }\:{dt}\:\:\:\:{witht}>\mathrm{2}\:\:{changement}\:\:{x}^{{t}} \:={u}\:{give} \\ $$$${x}\:={u}^{\frac{\mathrm{1}}{{t}}} \:\Rightarrow{f}\left({t}\right)\:=\int_{\mathrm{0}} ^{\infty} \:\:\frac{\left({u}^{\frac{\mathrm{1}}{{t}}} \right)^{{t}−\mathrm{2}} }{\mathrm{1}+{u}}\:\frac{\mathrm{1}}{{t}}\:{u}^{\frac{\mathrm{1}}{{t}}−\mathrm{1}} \:{du} \\ $$$$=\frac{\mathrm{1}}{{t}}\int_{\mathrm{0}} ^{\infty} \:\:\:\:\frac{{u}^{\frac{{t}−\mathrm{2}}{{t}}+\frac{\mathrm{1}}{{t}}−\mathrm{1}} }{\mathrm{1}+{u}}\:{du}\:=\frac{\mathrm{1}}{{t}}\int_{\mathrm{0}} ^{\infty} \:\:\:\frac{{u}^{\frac{{t}−\mathrm{1}}{{t}}\:\:\:−\mathrm{1}} }{\mathrm{1}+{u}}\:{du}\:\:\:{we}\:{have}\:{t}>\mathrm{2}\:\Rightarrow \\ $$$$\frac{\mathrm{1}}{{t}}<\frac{\mathrm{1}}{\mathrm{2}}\:\Rightarrow−\frac{\mathrm{1}}{{t}}>−\frac{\mathrm{1}}{\mathrm{2}}\:\Rightarrow\mathrm{1}−\frac{\mathrm{1}}{{t}}>\frac{\mathrm{1}}{\mathrm{2}}\:\Rightarrow\:\frac{{t}−\mathrm{1}}{{t}}>\frac{\mathrm{1}}{\mathrm{2}}\:{and}\:\frac{{t}−\mathrm{1}}{{t}}=\mathrm{1}−\frac{\mathrm{1}}{{t}}<\mathrm{1}\:\Rightarrow \\ $$$${f}\left({t}\right)=\frac{\mathrm{1}}{{t}}\:\frac{\pi}{{sin}\left(\pi\left(\frac{{t}−\mathrm{1}}{{t}}\right)\right)}\:=\frac{\pi}{{t}\:{sin}\left(\pi−\frac{\pi}{{t}}\right)}\:=\frac{\pi}{{t}\:{sin}\left(\frac{\pi}{{t}}\right)}\: \\ $$$$\int_{\mathrm{0}} ^{\infty} \:\:\frac{{x}^{\mathrm{2017}} }{\mathrm{1}+{x}^{\mathrm{2019}} }\:=\int_{\mathrm{0}} ^{\infty} \:\frac{{x}^{\mathrm{2019}\:−\mathrm{2}} }{\mathrm{1}+{x}^{\mathrm{2919}} }\:={f}\left(\mathrm{2019}\right)\:=\frac{\pi}{\mathrm{2019}\:{sin}\left(\frac{\pi}{\mathrm{2019}}\right)}\:={A} \\ $$$${B}\:={f}\left(\mathrm{2021}\right)\:=\frac{\pi}{\mathrm{2021}\:{sin}\left(\frac{\pi}{\mathrm{2021}}\right)} \\ $$
Commented by mathmax by abdo last updated on 12/Jul/19
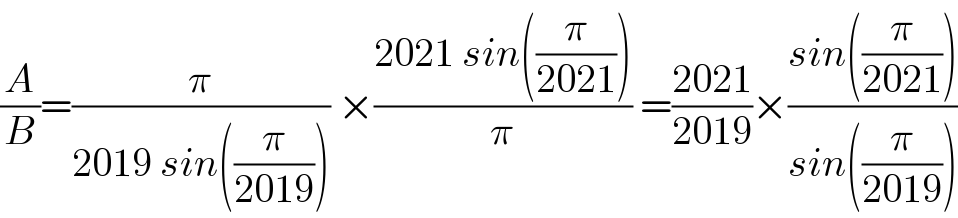
(A/B)=(π/(2019 sin((π/(2019))))) ×((2021 sin((π/(2021))))/π) =((2021)/(2019))×((sin((π/(2021))))/(sin((π/(2019)))))
$$\frac{{A}}{{B}}=\frac{\pi}{\mathrm{2019}\:{sin}\left(\frac{\pi}{\mathrm{2019}}\right)}\:×\frac{\mathrm{2021}\:{sin}\left(\frac{\pi}{\mathrm{2021}}\right)}{\pi}\:=\frac{\mathrm{2021}}{\mathrm{2019}}×\frac{{sin}\left(\frac{\pi}{\mathrm{2021}}\right)}{{sin}\left(\frac{\pi}{\mathrm{2019}}\right)} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *