Question Number 128496 by mathmax by abdo last updated on 07/Jan/21
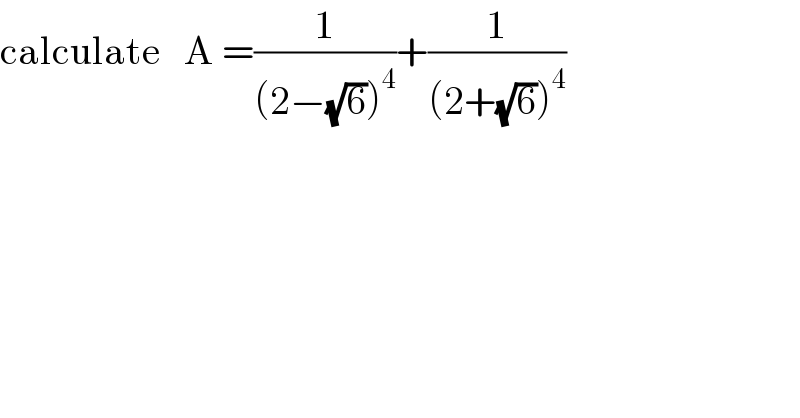
$$\mathrm{calculate}\:\:\:\mathrm{A}\:=\frac{\mathrm{1}}{\left(\mathrm{2}−\sqrt{\mathrm{6}}\right)^{\mathrm{4}} }+\frac{\mathrm{1}}{\left(\mathrm{2}+\sqrt{\mathrm{6}}\right)^{\mathrm{4}} } \\ $$
Commented by liberty last updated on 08/Jan/21
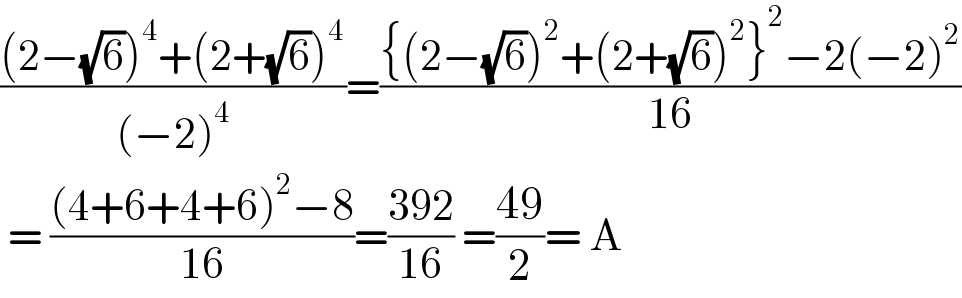
$$\frac{\left(\mathrm{2}−\sqrt{\mathrm{6}}\right)^{\mathrm{4}} +\left(\mathrm{2}+\sqrt{\mathrm{6}}\right)^{\mathrm{4}} }{\left(−\mathrm{2}\right)^{\mathrm{4}} }=\frac{\left\{\left(\mathrm{2}−\sqrt{\mathrm{6}}\right)^{\mathrm{2}} +\left(\mathrm{2}+\sqrt{\mathrm{6}}\right)^{\mathrm{2}} \right\}^{\mathrm{2}} −\mathrm{2}\left(−\mathrm{2}\right)^{\mathrm{2}} }{\mathrm{16}} \\ $$$$\:=\:\frac{\left(\mathrm{4}+\mathrm{6}+\mathrm{4}+\mathrm{6}\right)^{\mathrm{2}} −\mathrm{8}}{\mathrm{16}}=\frac{\mathrm{392}}{\mathrm{16}}\:=\frac{\mathrm{49}}{\mathrm{2}}=\:\mathrm{A} \\ $$
