Question Number 85641 by abdomathmax last updated on 23/Mar/20
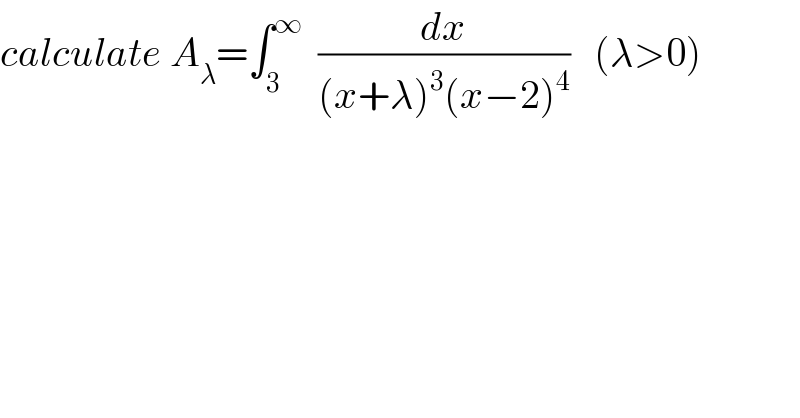
$${calculate}\:{A}_{\lambda} =\int_{\mathrm{3}} ^{\infty} \:\:\frac{{dx}}{\left({x}+\lambda\right)^{\mathrm{3}} \left({x}−\mathrm{2}\right)^{\mathrm{4}} }\:\:\:\left(\lambda>\mathrm{0}\right) \\ $$
Commented by mathmax by abdo last updated on 24/Mar/20
![A_λ =∫_3 ^(+∞) (dx/((((x+λ)/(x−2)))^3 (x−2)^7 )) changement ((x+λ)/(x−2))=t give x+λ =tx−2t ⇒(1−t)x=−2t−λ ⇒x=((−2t−λ)/(1−t)) =((2t+λ)/(t−1)) ⇒ (dx/dt) =((2(t−1)−(2t+λ))/((t−1)^2 )) =((2t−2−2t−λ)/((t−1)^2 )) =((−2−λ)/((t−1)^2 )) x−2 =((2t+λ)/(t−1))−2 =((2t+λ−2t+2)/(t−1)) =((λ+2)/(t−1)) ⇒ A_λ =− ∫_(3+λ) ^1 (1/(t^3 (((λ+2)/(t−1)))^7 ))×((λ+2)/((t−1)^2 ))dt =(1/((λ+2)^6 ))∫_1 ^(3+λ) (dt/(t^3 (((λ+2)/(t−1)))^(−5) )) =(1/((λ+2)))∫_1 ^(3+λ) (((t−1)^5 )/t^3 )dt ⇒ (λ+2)A_λ =∫_1 ^(3+λ) ((Σ_(k=0) ^5 C_5 ^k t^k (−1)^(5−k) )/t^3 )dt =−∫_1 ^(3+λ) Σ_(k=0) ^5 (−1)^k C_5 ^k t^(k−3) dt =−Σ_(k=0) ^5 (−1)^k C_5 ^k ∫_1 ^(3+λ) t^(k−3) dt =−Σ_(k=0 and k≠2) ^5 (−1)^k C_5 ^k [(1/(k−2))t^(k−2) ]_1 ^(3+λ) −C_5 ^2 ∫_1 ^(3+λ) (dt/t) =−Σ_(k=0) ^5 (((−1)^k C_5 ^k )/(k−2)){ (3+λ)^(k−2) −1}−C_5 ^2 {ln∣3+λ∣} ⇒ A_λ =−(1/(λ+2))Σ_(k=0and k≠2) ^5 (((−1)^k C_5 ^k )/(k−2)){(3+λ)^(k−2) −1} −(1/(λ+2)) C_5 ^2 ln∣3+λ∣ .](https://www.tinkutara.com/question/Q85790.png)
$${A}_{\lambda} \:=\int_{\mathrm{3}} ^{+\infty} \:\frac{{dx}}{\left(\frac{{x}+\lambda}{{x}−\mathrm{2}}\right)^{\mathrm{3}} \:\left({x}−\mathrm{2}\right)^{\mathrm{7}} }\:{changement}\:\frac{{x}+\lambda}{{x}−\mathrm{2}}={t}\:{give} \\ $$$${x}+\lambda\:={tx}−\mathrm{2}{t}\:\Rightarrow\left(\mathrm{1}−{t}\right){x}=−\mathrm{2}{t}−\lambda\:\Rightarrow{x}=\frac{−\mathrm{2}{t}−\lambda}{\mathrm{1}−{t}}\:=\frac{\mathrm{2}{t}+\lambda}{{t}−\mathrm{1}}\:\Rightarrow \\ $$$$\frac{{dx}}{{dt}}\:=\frac{\mathrm{2}\left({t}−\mathrm{1}\right)−\left(\mathrm{2}{t}+\lambda\right)}{\left({t}−\mathrm{1}\right)^{\mathrm{2}} }\:=\frac{\mathrm{2}{t}−\mathrm{2}−\mathrm{2}{t}−\lambda}{\left({t}−\mathrm{1}\right)^{\mathrm{2}} }\:=\frac{−\mathrm{2}−\lambda}{\left({t}−\mathrm{1}\right)^{\mathrm{2}} } \\ $$$${x}−\mathrm{2}\:=\frac{\mathrm{2}{t}+\lambda}{{t}−\mathrm{1}}−\mathrm{2}\:=\frac{\mathrm{2}{t}+\lambda−\mathrm{2}{t}+\mathrm{2}}{{t}−\mathrm{1}}\:=\frac{\lambda+\mathrm{2}}{{t}−\mathrm{1}}\:\Rightarrow \\ $$$${A}_{\lambda} =−\:\int_{\mathrm{3}+\lambda} ^{\mathrm{1}} \:\frac{\mathrm{1}}{{t}^{\mathrm{3}} \left(\frac{\lambda+\mathrm{2}}{{t}−\mathrm{1}}\right)^{\mathrm{7}} }×\frac{\lambda+\mathrm{2}}{\left({t}−\mathrm{1}\right)^{\mathrm{2}} }{dt} \\ $$$$=\frac{\mathrm{1}}{\left(\lambda+\mathrm{2}\right)^{\mathrm{6}} }\int_{\mathrm{1}} ^{\mathrm{3}+\lambda} \:\:\:\:\frac{{dt}}{{t}^{\mathrm{3}} \left(\frac{\lambda+\mathrm{2}}{{t}−\mathrm{1}}\right)^{−\mathrm{5}} }\:=\frac{\mathrm{1}}{\left(\lambda+\mathrm{2}\right)}\int_{\mathrm{1}} ^{\mathrm{3}+\lambda} \:\frac{\left({t}−\mathrm{1}\right)^{\mathrm{5}} }{{t}^{\mathrm{3}} }{dt}\:\Rightarrow \\ $$$$\left(\lambda+\mathrm{2}\right){A}_{\lambda} \:=\int_{\mathrm{1}} ^{\mathrm{3}+\lambda} \:\frac{\sum_{{k}=\mathrm{0}} ^{\mathrm{5}} \:{C}_{\mathrm{5}} ^{{k}} \:{t}^{{k}} \left(−\mathrm{1}\right)^{\mathrm{5}−{k}} }{{t}^{\mathrm{3}} }{dt} \\ $$$$=−\int_{\mathrm{1}} ^{\mathrm{3}+\lambda} \:\sum_{{k}=\mathrm{0}} ^{\mathrm{5}} \:\left(−\mathrm{1}\right)^{{k}} \:{C}_{\mathrm{5}} ^{{k}} \:{t}^{{k}−\mathrm{3}} \:{dt} \\ $$$$=−\sum_{{k}=\mathrm{0}} ^{\mathrm{5}} \:\left(−\mathrm{1}\right)^{{k}} {C}_{\mathrm{5}} ^{{k}} \:\:\int_{\mathrm{1}} ^{\mathrm{3}+\lambda} \:\:{t}^{{k}−\mathrm{3}} \:{dt} \\ $$$$=−\sum_{{k}=\mathrm{0}\:{and}\:{k}\neq\mathrm{2}} ^{\mathrm{5}} \:\left(−\mathrm{1}\right)^{{k}} \:{C}_{\mathrm{5}} ^{{k}} \:\:\:\left[\frac{\mathrm{1}}{{k}−\mathrm{2}}{t}^{{k}−\mathrm{2}} \right]_{\mathrm{1}} ^{\mathrm{3}+\lambda} \:−{C}_{\mathrm{5}} ^{\mathrm{2}} \:\int_{\mathrm{1}} ^{\mathrm{3}+\lambda} \:\frac{{dt}}{{t}} \\ $$$$=−\sum_{{k}=\mathrm{0}} ^{\mathrm{5}} \:\frac{\left(−\mathrm{1}\right)^{{k}} \:{C}_{\mathrm{5}} ^{{k}} }{{k}−\mathrm{2}}\left\{\:\left(\mathrm{3}+\lambda\right)^{{k}−\mathrm{2}} −\mathrm{1}\right\}−{C}_{\mathrm{5}} ^{\mathrm{2}} \left\{{ln}\mid\mathrm{3}+\lambda\mid\right\}\:\Rightarrow \\ $$$${A}_{\lambda} =−\frac{\mathrm{1}}{\lambda+\mathrm{2}}\sum_{{k}=\mathrm{0}{and}\:{k}\neq\mathrm{2}} ^{\mathrm{5}} \:\:\:\frac{\left(−\mathrm{1}\right)^{{k}} \:{C}_{\mathrm{5}} ^{{k}} }{{k}−\mathrm{2}}\left\{\left(\mathrm{3}+\lambda\right)^{{k}−\mathrm{2}} −\mathrm{1}\right\} \\ $$$$−\frac{\mathrm{1}}{\lambda+\mathrm{2}}\:{C}_{\mathrm{5}} ^{\mathrm{2}} {ln}\mid\mathrm{3}+\lambda\mid\:. \\ $$$$ \\ $$
Commented by mathmax by abdo last updated on 24/Mar/20

$$\lambda\neq−\mathrm{2} \\ $$
