Question Number 79646 by abdomathmax last updated on 27/Jan/20
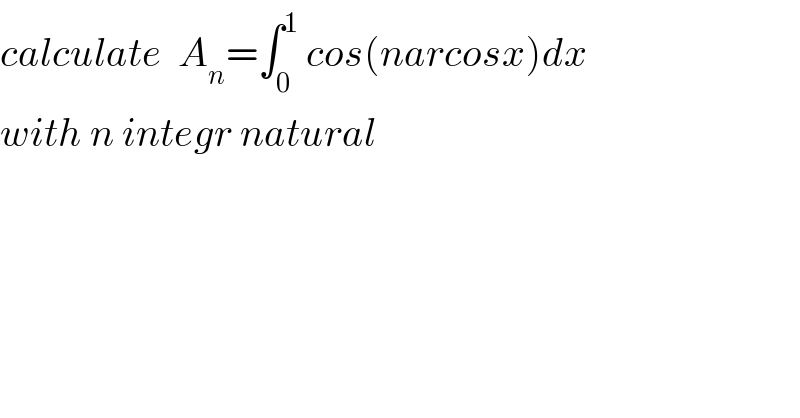
$${calculate}\:\:{A}_{{n}} =\int_{\mathrm{0}} ^{\mathrm{1}} \:{cos}\left({narcosx}\right){dx} \\ $$$${with}\:{n}\:{integr}\:{natural} \\ $$
Commented by abdomathmax last updated on 12/Mar/20
![changement arcosx=t give x=cost ⇒ A_n =∫_(π/2) ^0 cos(nt)(−sint)dt =∫_0 ^(π/2) sint cos(nt)dt we have sint cos(nt) =cos((π/2)−t)cos(nt) =(1/2){ cos((π/2)−t+nt)+cos(nt−(π/2)+t)} =(1/2){ cos((n−1)t+(π/2))+cos((π/2)−(n+1)t) =(1/2){ −sin(n−1)t +sin(n+1)t} ⇒ A_n =(1/2)∫_0 ^(π/2) sin(n+1)t dt−(1/2)∫_0 ^(π/2) sin(n−1)dt =−(1/(2(n+1)))[cos(n+1)t]_0 ^(π/2) +(1/(2(n−1)))[cos(n−1)t]_0 ^(π/2) =−(1/(2(n+1))){ cos(n+1)(π/2)−1} +(1/(2(n−1))){ cos(n−1)(π/2)−1} (n≠1) A_1 =∫_0 ^1 xdx =(1/2)](https://www.tinkutara.com/question/Q84434.png)
$${changement}\:{arcosx}={t}\:{give}\:{x}={cost}\:\Rightarrow \\ $$$${A}_{{n}} =\int_{\frac{\pi}{\mathrm{2}}} ^{\mathrm{0}} \:{cos}\left({nt}\right)\left(−{sint}\right){dt} \\ $$$$=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:{sint}\:{cos}\left({nt}\right){dt} \\ $$$${we}\:{have}\:{sint}\:{cos}\left({nt}\right) \\ $$$$={cos}\left(\frac{\pi}{\mathrm{2}}−{t}\right){cos}\left({nt}\right)\:=\frac{\mathrm{1}}{\mathrm{2}}\left\{\:{cos}\left(\frac{\pi}{\mathrm{2}}−{t}+{nt}\right)+{cos}\left({nt}−\frac{\pi}{\mathrm{2}}+{t}\right)\right\} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\left\{\:{cos}\left(\left({n}−\mathrm{1}\right){t}+\frac{\pi}{\mathrm{2}}\right)+{cos}\left(\frac{\pi}{\mathrm{2}}−\left({n}+\mathrm{1}\right){t}\right)\right. \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\left\{\:−{sin}\left({n}−\mathrm{1}\right){t}\:\:+{sin}\left({n}+\mathrm{1}\right){t}\right\}\:\Rightarrow \\ $$$${A}_{{n}} =\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:{sin}\left({n}+\mathrm{1}\right){t}\:{dt}−\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:{sin}\left({n}−\mathrm{1}\right){dt} \\ $$$$=−\frac{\mathrm{1}}{\mathrm{2}\left({n}+\mathrm{1}\right)}\left[{cos}\left({n}+\mathrm{1}\right){t}\right]_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:+\frac{\mathrm{1}}{\mathrm{2}\left({n}−\mathrm{1}\right)}\left[{cos}\left({n}−\mathrm{1}\right){t}\right]_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \\ $$$$=−\frac{\mathrm{1}}{\mathrm{2}\left({n}+\mathrm{1}\right)}\left\{\:{cos}\left({n}+\mathrm{1}\right)\frac{\pi}{\mathrm{2}}−\mathrm{1}\right\} \\ $$$$+\frac{\mathrm{1}}{\mathrm{2}\left({n}−\mathrm{1}\right)}\left\{\:{cos}\left({n}−\mathrm{1}\right)\frac{\pi}{\mathrm{2}}−\mathrm{1}\right\}\:\:\:\left({n}\neq\mathrm{1}\right) \\ $$$${A}_{\mathrm{1}} =\int_{\mathrm{0}} ^{\mathrm{1}} {xdx}\:=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$ \\ $$
