Menu Close

calculate-A-n-0-dx-x-2-1-x-2-2-x-2-n-wth-n-integr-natural-and-n-1-

Tinku Tara 0 Comments
Pin




Question Number 122323 by mathmax by abdo last updated on 15/Nov/20
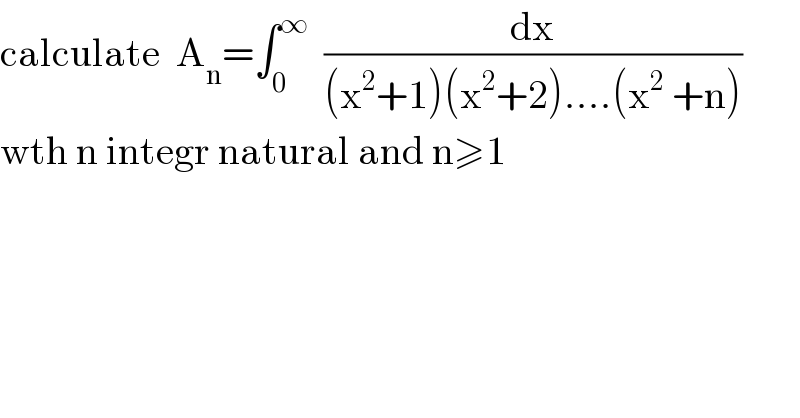
calculate A_n =∫_0 ^∞ (dx/((x^2 +1)(x^2 +2)....(x^2 +n))) wth n integr natural and n≥1
$$\mathrm{calculate}\:\:\mathrm{A}_{\mathrm{n}} =\int_{\mathrm{0}} ^{\infty} \:\:\frac{\mathrm{dx}}{\left(\mathrm{x}^{\mathrm{2}} +\mathrm{1}\right)\left(\mathrm{x}^{\mathrm{2}} +\mathrm{2}\right)….\left(\mathrm{x}^{\mathrm{2}} \:+\mathrm{n}\right)} \\ $$$$\mathrm{wth}\:\mathrm{n}\:\mathrm{integr}\:\mathrm{natural}\:\mathrm{and}\:\mathrm{n}\geqslant\mathrm{1} \\ $$
Commented by Dwaipayan Shikari last updated on 16/Nov/20
∫_0 ^∞ ((1/(x^2 +1))−(1/(x^2 +2)))dx =(π/2)(1−(1/( (√2)))) ∫_0 ^∞ (1/((x^2 +1)(x^2 +2)(x^2 +3)))=(1/2)∫_0 ^∞ (1/((x^2 +1)))−(1/((x^2 +3)))−∫_0 ^∞ (1/((x^2 +2)))−(1/((x^2 +3))) =(1/2)((π/2)−(π/(2(√3))))−((π/( 2(√2)))−(π/(2(√3)))) = (π/4)−(π/(2(√2)))+(π/(4(√3))) ∫_0 ^∞ (1/((x^2 +1)(x^2 +2)(x^2 +3)(x^2 +4)))dx =(1/3)∫_0 ^∞ (1/((x^2 +1)(x^2 +2)(x^2 +3)))−(1/3)∫_0 ^∞ (1/((x^2 +2)(x^2 +3)(x^2 +4))) =(π/(12))−(π/(6(√2)))+(π/(6(√3)))−(1/6)∫_0 ^∞ (1/(x^2 +2))−(1/(x^2 +4))+(1/3)∫_0 ^∞ (1/(x^2 +3))−(1/(x^2 +4)) =(π/(12))−(π/(6(√2)))+(π/(6(√3)))−(1/6)((π/(2(√2)))−(π/( 2(√4))))+(1/3)((π/(2(√3)))−(π/(2(√4)))) =(π/(12))−(π/(4(√2)))+(π/(3(√3))) ....
$$\int_{\mathrm{0}} ^{\infty} \left(\frac{\mathrm{1}}{{x}^{\mathrm{2}} +\mathrm{1}}−\frac{\mathrm{1}}{{x}^{\mathrm{2}} +\mathrm{2}}\right){dx} \\ $$$$=\frac{\pi}{\mathrm{2}}\left(\mathrm{1}−\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\right) \\ $$$$\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{1}}{\left({x}^{\mathrm{2}} +\mathrm{1}\right)\left({x}^{\mathrm{2}} +\mathrm{2}\right)\left({x}^{\mathrm{2}} +\mathrm{3}\right)}=\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{1}}{\left({x}^{\mathrm{2}} +\mathrm{1}\right)}−\frac{\mathrm{1}}{\left({x}^{\mathrm{2}} +\mathrm{3}\right)}−\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{1}}{\left({x}^{\mathrm{2}} +\mathrm{2}\right)}−\frac{\mathrm{1}}{\left({x}^{\mathrm{2}} +\mathrm{3}\right)} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{\pi}{\mathrm{2}}−\frac{\pi}{\mathrm{2}\sqrt{\mathrm{3}}}\right)−\left(\frac{\pi}{\:\mathrm{2}\sqrt{\mathrm{2}}}−\frac{\pi}{\mathrm{2}\sqrt{\mathrm{3}}}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\:\frac{\pi}{\mathrm{4}}−\frac{\pi}{\mathrm{2}\sqrt{\mathrm{2}}}+\frac{\pi}{\mathrm{4}\sqrt{\mathrm{3}}} \\ $$$$\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{1}}{\left({x}^{\mathrm{2}} +\mathrm{1}\right)\left({x}^{\mathrm{2}} +\mathrm{2}\right)\left({x}^{\mathrm{2}} +\mathrm{3}\right)\left({x}^{\mathrm{2}} +\mathrm{4}\right)}{dx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{3}}\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{1}}{\left({x}^{\mathrm{2}} +\mathrm{1}\right)\left({x}^{\mathrm{2}} +\mathrm{2}\right)\left({x}^{\mathrm{2}} +\mathrm{3}\right)}−\frac{\mathrm{1}}{\mathrm{3}}\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{1}}{\left({x}^{\mathrm{2}} +\mathrm{2}\right)\left({x}^{\mathrm{2}} +\mathrm{3}\right)\left({x}^{\mathrm{2}} +\mathrm{4}\right)} \\ $$$$=\frac{\pi}{\mathrm{12}}−\frac{\pi}{\mathrm{6}\sqrt{\mathrm{2}}}+\frac{\pi}{\mathrm{6}\sqrt{\mathrm{3}}}−\frac{\mathrm{1}}{\mathrm{6}}\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{1}}{{x}^{\mathrm{2}} +\mathrm{2}}−\frac{\mathrm{1}}{{x}^{\mathrm{2}} +\mathrm{4}}+\frac{\mathrm{1}}{\mathrm{3}}\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{1}}{{x}^{\mathrm{2}} +\mathrm{3}}−\frac{\mathrm{1}}{{x}^{\mathrm{2}} +\mathrm{4}} \\ $$$$=\frac{\pi}{\mathrm{12}}−\frac{\pi}{\mathrm{6}\sqrt{\mathrm{2}}}+\frac{\pi}{\mathrm{6}\sqrt{\mathrm{3}}}−\frac{\mathrm{1}}{\mathrm{6}}\left(\frac{\pi}{\mathrm{2}\sqrt{\mathrm{2}}}−\frac{\pi}{\:\mathrm{2}\sqrt{\mathrm{4}}}\right)+\frac{\mathrm{1}}{\mathrm{3}}\left(\frac{\pi}{\mathrm{2}\sqrt{\mathrm{3}}}−\frac{\pi}{\mathrm{2}\sqrt{\mathrm{4}}}\right) \\ $$$$=\frac{\pi}{\mathrm{12}}−\frac{\pi}{\mathrm{4}\sqrt{\mathrm{2}}}+\frac{\pi}{\mathrm{3}\sqrt{\mathrm{3}}} \\ $$$$…. \\ $$$$ \\ $$
Answered by mathmax by abdo last updated on 16/Nov/20
let decompose F(u)=(1/((u+1)(u+2)....(u+n))) =(1/(Π_(k=1) ^n (u+k))) F(u)=Σ_(k=1) ^n (a_k /(u+k)) with a_k =lim_(u→−k) (u+k)F(u) we have F(u) =(1/((u+1)....(u+k−1)(u+k)(u+k+1)...(u+n))) (u+k)F(u) =(1/((u+1)(u+2)...(u+k−1)(u+k+1)....(u+n))) ⇒ a_k =(1/((−k+1)(−k+2)....(−1)(−k+k+1)(−k+k+2)...(−k+n))) =(1/((−1)^(k−1) (k−1)!))×(1/((n−k)!)) =(((−1)^(k−1) )/((k−1)!(n−k)!)) ⇒ F(u)=Σ_(k=1) ^n (((−1)^(k−1) )/((k−1)!(n−k)!(u+k))) 2A_n =∫_(−∞) ^(+∞) F(x^2 )dx =Σ_(k=1) ^n (((−1)^(k−1) )/((k−1)!(n−k)!))∫_(−∞) ^(+∞) (dx/(x^2 +k)) ∫_(−∞) ^(+∞) (dx/(x^2 +k)) =∫_(−∞) ^(+∞) (dx/((x−i(√k))(x+i(√k)))) =2iπ Res(f,i(√k)) =2iπ×(1/(2i(√k))) =(π/( (√k))) ⇒ A_n =(π/2) Σ_(k=1) ^n (((−1)^(k−1) )/((k−1)!(n−k)!(√k)))
$$\mathrm{let}\:\mathrm{decompose}\:\mathrm{F}\left(\mathrm{u}\right)=\frac{\mathrm{1}}{\left(\mathrm{u}+\mathrm{1}\right)\left(\mathrm{u}+\mathrm{2}\right)….\left(\mathrm{u}+\mathrm{n}\right)}\:=\frac{\mathrm{1}}{\prod_{\mathrm{k}=\mathrm{1}} ^{\mathrm{n}} \left(\mathrm{u}+\mathrm{k}\right)} \\ $$$$\mathrm{F}\left(\mathrm{u}\right)=\sum_{\mathrm{k}=\mathrm{1}} ^{\mathrm{n}} \:\frac{\mathrm{a}_{\mathrm{k}} }{\mathrm{u}+\mathrm{k}}\:\:\:\:\mathrm{with}\:\mathrm{a}_{\mathrm{k}} =\mathrm{lim}_{\mathrm{u}\rightarrow−\mathrm{k}} \:\:\left(\mathrm{u}+\mathrm{k}\right)\mathrm{F}\left(\mathrm{u}\right) \\ $$$$\mathrm{we}\:\mathrm{have}\:\mathrm{F}\left(\mathrm{u}\right)\:=\frac{\mathrm{1}}{\left(\mathrm{u}+\mathrm{1}\right)….\left(\mathrm{u}+\mathrm{k}−\mathrm{1}\right)\left(\mathrm{u}+\mathrm{k}\right)\left(\mathrm{u}+\mathrm{k}+\mathrm{1}\right)…\left(\mathrm{u}+\mathrm{n}\right)} \\ $$$$\left(\mathrm{u}+\mathrm{k}\right)\mathrm{F}\left(\mathrm{u}\right)\:=\frac{\mathrm{1}}{\left(\mathrm{u}+\mathrm{1}\right)\left(\mathrm{u}+\mathrm{2}\right)…\left(\mathrm{u}+\mathrm{k}−\mathrm{1}\right)\left(\mathrm{u}+\mathrm{k}+\mathrm{1}\right)….\left(\mathrm{u}+\mathrm{n}\right)}\:\Rightarrow \\ $$$$\mathrm{a}_{\mathrm{k}} =\frac{\mathrm{1}}{\left(−\mathrm{k}+\mathrm{1}\right)\left(−\mathrm{k}+\mathrm{2}\right)….\left(−\mathrm{1}\right)\left(−\mathrm{k}+\mathrm{k}+\mathrm{1}\right)\left(−\mathrm{k}+\mathrm{k}+\mathrm{2}\right)…\left(−\mathrm{k}+\mathrm{n}\right)} \\ $$$$=\frac{\mathrm{1}}{\left(−\mathrm{1}\right)^{\mathrm{k}−\mathrm{1}} \left(\mathrm{k}−\mathrm{1}\right)!}×\frac{\mathrm{1}}{\left(\mathrm{n}−\mathrm{k}\right)!}\:=\frac{\left(−\mathrm{1}\right)^{\mathrm{k}−\mathrm{1}} }{\left(\mathrm{k}−\mathrm{1}\right)!\left(\mathrm{n}−\mathrm{k}\right)!}\:\Rightarrow \\ $$$$\mathrm{F}\left(\mathrm{u}\right)=\sum_{\mathrm{k}=\mathrm{1}} ^{\mathrm{n}} \:\frac{\left(−\mathrm{1}\right)^{\mathrm{k}−\mathrm{1}} }{\left(\mathrm{k}−\mathrm{1}\right)!\left(\mathrm{n}−\mathrm{k}\right)!\left(\mathrm{u}+\mathrm{k}\right)} \\ $$$$\mathrm{2A}_{\mathrm{n}} =\int_{−\infty} ^{+\infty} \mathrm{F}\left(\mathrm{x}^{\mathrm{2}} \right)\mathrm{dx}\:=\sum_{\mathrm{k}=\mathrm{1}} ^{\mathrm{n}} \:\frac{\left(−\mathrm{1}\right)^{\mathrm{k}−\mathrm{1}} }{\left(\mathrm{k}−\mathrm{1}\right)!\left(\mathrm{n}−\mathrm{k}\right)!}\int_{−\infty} ^{+\infty} \:\frac{\mathrm{dx}}{\mathrm{x}^{\mathrm{2}} \:+\mathrm{k}} \\ $$$$\int_{−\infty} ^{+\infty} \:\frac{\mathrm{dx}}{\mathrm{x}^{\mathrm{2}} \:+\mathrm{k}}\:=\int_{−\infty} ^{+\infty} \:\frac{\mathrm{dx}}{\left(\mathrm{x}−\mathrm{i}\sqrt{\mathrm{k}}\right)\left(\mathrm{x}+\mathrm{i}\sqrt{\mathrm{k}}\right)}\:=\mathrm{2i}\pi\:\mathrm{Res}\left(\mathrm{f},\mathrm{i}\sqrt{\mathrm{k}}\right) \\ $$$$=\mathrm{2i}\pi×\frac{\mathrm{1}}{\mathrm{2i}\sqrt{\mathrm{k}}}\:=\frac{\pi}{\:\sqrt{\mathrm{k}}}\:\Rightarrow\:\mathrm{A}_{\mathrm{n}} =\frac{\pi}{\mathrm{2}}\:\sum_{\mathrm{k}=\mathrm{1}} ^{\mathrm{n}} \:\frac{\left(−\mathrm{1}\right)^{\mathrm{k}−\mathrm{1}} }{\left(\mathrm{k}−\mathrm{1}\right)!\left(\mathrm{n}−\mathrm{k}\right)!\sqrt{\mathrm{k}}} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *