calculate-A-n-dx-x-2-1-x-2-2-x-2-n-with-n-integr-natural-and-n-1-

Question Number 64166 by mathmax by abdo last updated on 14/Jul/19

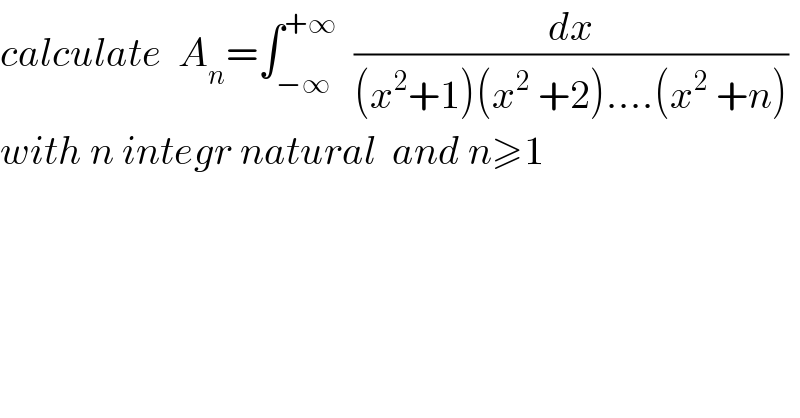
c a l c u l a t e A_{n} = \int_{- \infty}^{+ \infty} \frac{d x}{(x^{2} + 1) (x^{2} + 2) \dots . (x^{2} + n)}

w i t h n i n t e g r n a t u r a l a n d n ⩾ 1

Answered by Eminem last updated on 14/Jul/19

f (z) = \frac{d z}{(z^{2} + 1) \dots \dots (z^{2} + n)}

A_{n} = 2 i π R e (z k = i \sqrt{k}, k \in [1 . . n])

r e s (f . i \sqrt{k}) = \frac{1}{2 i \sqrt{k} \underset{j = 1}{\prod^{n, k \neq j}} (1 - j)} = \frac{1 - k}{2 i \sqrt{k} {(- 1)}^{n} (n - 1)!}

A_{n} = 2 i π \underset{k = 2}{\sum^{n}} \frac{(1 - k)}{2 i \sqrt{k} (n - 1)!} + \frac{2 i π}{2 i {(- 1)}^{n} (n - 1)!}

Facebook Tweet Pin