Menu Close

calculate-A-n-k-0-n-k-C-n-k-B-n-k-0-n-k-2-C-n-k-C-n-k-0-n-k-3-C-n-k-

Tinku Tara 0 Comments
Pin




Question Number 43007 by abdo.msup.com last updated on 06/Sep/18
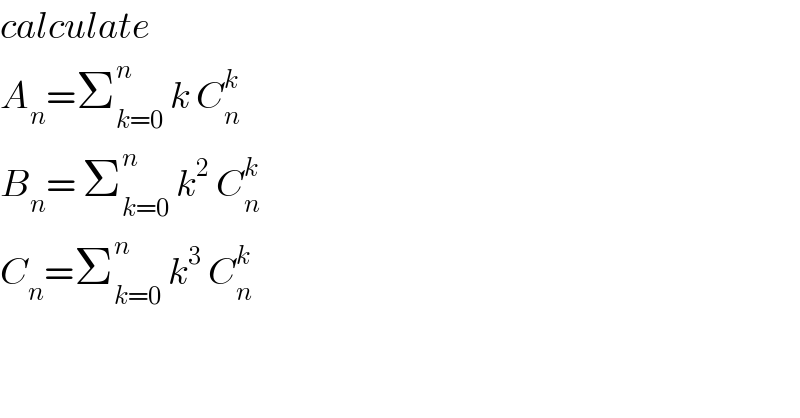
calculate A_n =Σ_(k=0) ^n k C_n ^k B_n = Σ_(k=0) ^n k^2 C_n ^k C_n =Σ_(k=0) ^n k^3 C_n ^k
$${calculate}\: \\ $$$${A}_{{n}} =\sum_{{k}=\mathrm{0}} ^{{n}} \:{k}\:{C}_{{n}} ^{{k}} \\ $$$${B}_{{n}} =\:\sum_{{k}=\mathrm{0}} ^{{n}} \:{k}^{\mathrm{2}} \:{C}_{{n}} ^{{k}} \\ $$$${C}_{{n}} =\sum_{{k}=\mathrm{0}} ^{{n}} \:{k}^{\mathrm{3}} \:{C}_{{n}} ^{{k}} \\ $$
Commented by maxmathsup by imad last updated on 06/Sep/18
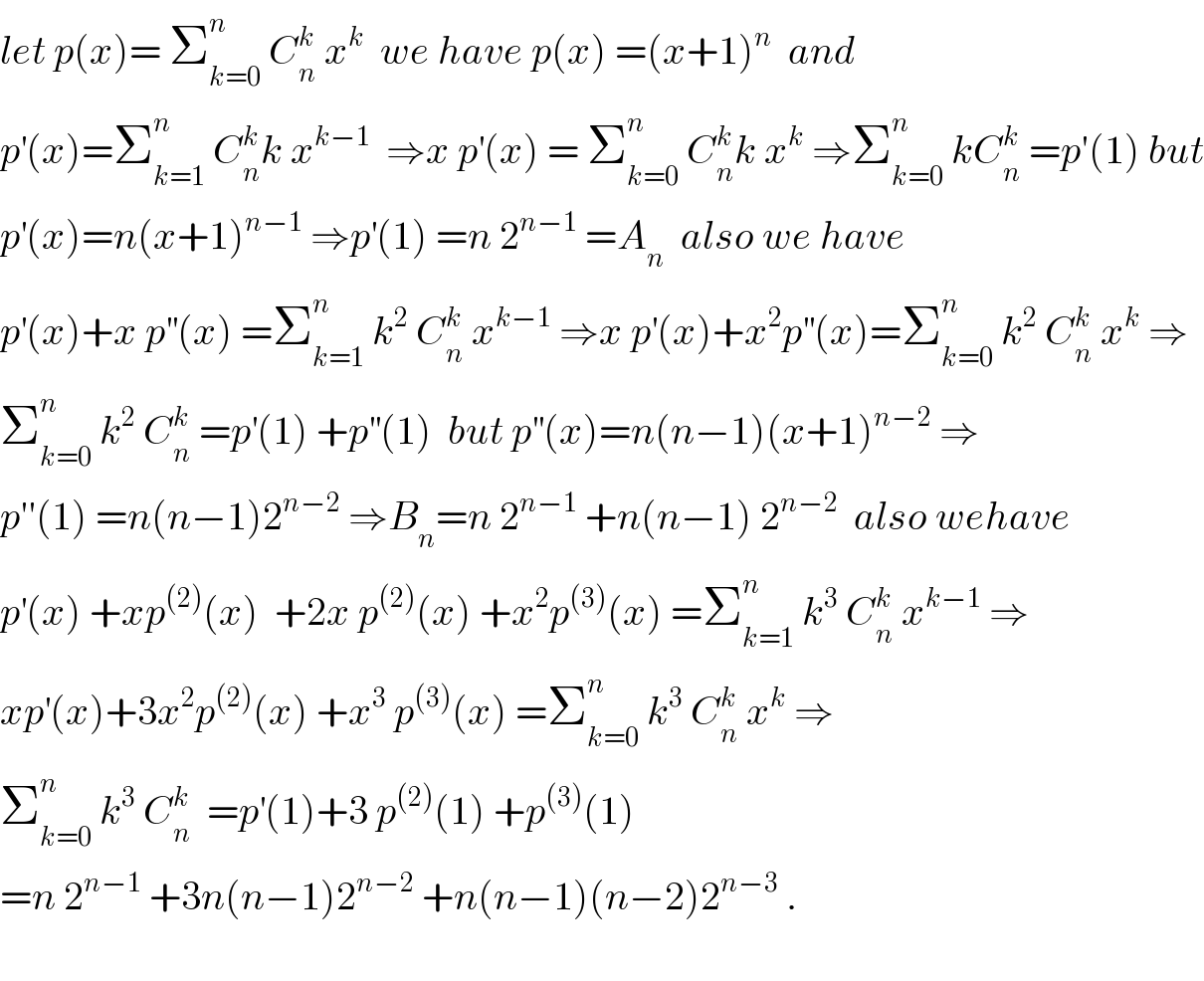
let p(x)= Σ_(k=0) ^n C_n ^k x^k we have p(x) =(x+1)^n and p^′ (x)=Σ_(k=1) ^n C_n ^k k x^(k−1) ⇒x p^′ (x) = Σ_(k=0) ^n C_n ^k k x^k ⇒Σ_(k=0) ^n kC_n ^k =p′(1) but p^′ (x)=n(x+1)^(n−1) ⇒p^′ (1) =n 2^(n−1) =A_n also we have p^′ (x)+x p^(′′) (x) =Σ_(k=1) ^n k^2 C_n ^k x^(k−1) ⇒x p^′ (x)+x^2 p^(′′) (x)=Σ_(k=0) ^n k^2 C_n ^k x^k ⇒ Σ_(k=0) ^n k^2 C_n ^k =p^′ (1) +p^(′′) (1) but p^(′′) (x)=n(n−1)(x+1)^(n−2) ⇒ p′′(1) =n(n−1)2^(n−2) ⇒B_n =n 2^(n−1) +n(n−1) 2^(n−2) also wehave p^′ (x) +xp^((2)) (x) +2x p^((2)) (x) +x^2 p^((3)) (x) =Σ_(k=1) ^n k^3 C_n ^k x^(k−1) ⇒ xp^′ (x)+3x^2 p^((2)) (x) +x^3 p^((3)) (x) =Σ_(k=0) ^n k^3 C_n ^k x^k ⇒ Σ_(k=0) ^n k^3 C_n ^k =p^′ (1)+3 p^((2)) (1) +p^((3)) (1) =n 2^(n−1) +3n(n−1)2^(n−2) +n(n−1)(n−2)2^(n−3) .
$${let}\:{p}\left({x}\right)=\:\sum_{{k}=\mathrm{0}} ^{{n}} \:{C}_{{n}} ^{{k}} \:{x}^{{k}} \:\:{we}\:{have}\:{p}\left({x}\right)\:=\left({x}+\mathrm{1}\right)^{{n}} \:\:{and}\: \\ $$$${p}^{'} \left({x}\right)=\sum_{{k}=\mathrm{1}} ^{{n}} \:{C}_{{n}} ^{{k}} {k}\:{x}^{{k}−\mathrm{1}} \:\:\Rightarrow{x}\:{p}^{'} \left({x}\right)\:=\:\sum_{{k}=\mathrm{0}} ^{{n}} \:{C}_{{n}} ^{{k}} {k}\:{x}^{{k}} \:\Rightarrow\sum_{{k}=\mathrm{0}} ^{{n}} \:{kC}_{{n}} ^{{k}} \:={p}'\left(\mathrm{1}\right)\:{but} \\ $$$${p}^{'} \left({x}\right)={n}\left({x}+\mathrm{1}\right)^{{n}−\mathrm{1}} \:\Rightarrow{p}^{'} \left(\mathrm{1}\right)\:={n}\:\mathrm{2}^{{n}−\mathrm{1}} \:={A}_{{n}} \:\:{also}\:{we}\:{have} \\ $$$${p}^{'} \left({x}\right)+{x}\:{p}^{''} \left({x}\right)\:=\sum_{{k}=\mathrm{1}} ^{{n}} \:{k}^{\mathrm{2}} \:{C}_{{n}} ^{{k}} \:{x}^{{k}−\mathrm{1}} \:\Rightarrow{x}\:{p}^{'} \left({x}\right)+{x}^{\mathrm{2}} {p}^{''} \left({x}\right)=\sum_{{k}=\mathrm{0}} ^{{n}} \:{k}^{\mathrm{2}} \:{C}_{{n}} ^{{k}} \:{x}^{{k}} \:\Rightarrow \\ $$$$\sum_{{k}=\mathrm{0}} ^{{n}} \:{k}^{\mathrm{2}} \:{C}_{{n}} ^{{k}} \:={p}^{'} \left(\mathrm{1}\right)\:+{p}^{''} \left(\mathrm{1}\right)\:\:{but}\:{p}^{''} \left({x}\right)={n}\left({n}−\mathrm{1}\right)\left({x}+\mathrm{1}\right)^{{n}−\mathrm{2}} \:\Rightarrow \\ $$$${p}''\left(\mathrm{1}\right)\:={n}\left({n}−\mathrm{1}\right)\mathrm{2}^{{n}−\mathrm{2}} \:\Rightarrow{B}_{{n}} ={n}\:\mathrm{2}^{{n}−\mathrm{1}} \:+{n}\left({n}−\mathrm{1}\right)\:\mathrm{2}^{{n}−\mathrm{2}} \:\:{also}\:{wehave} \\ $$$${p}^{'} \left({x}\right)\:+{xp}^{\left(\mathrm{2}\right)} \left({x}\right)\:\:+\mathrm{2}{x}\:{p}^{\left(\mathrm{2}\right)} \left({x}\right)\:+{x}^{\mathrm{2}} {p}^{\left(\mathrm{3}\right)} \left({x}\right)\:=\sum_{{k}=\mathrm{1}} ^{{n}} \:{k}^{\mathrm{3}} \:{C}_{{n}} ^{{k}} \:{x}^{{k}−\mathrm{1}} \:\Rightarrow \\ $$$${xp}^{'} \left({x}\right)+\mathrm{3}{x}^{\mathrm{2}} {p}^{\left(\mathrm{2}\right)} \left({x}\right)\:+{x}^{\mathrm{3}} \:{p}^{\left(\mathrm{3}\right)} \left({x}\right)\:=\sum_{{k}=\mathrm{0}} ^{{n}} \:{k}^{\mathrm{3}} \:{C}_{{n}} ^{{k}} \:{x}^{{k}} \:\Rightarrow \\ $$$$\sum_{{k}=\mathrm{0}} ^{{n}} \:{k}^{\mathrm{3}} \:{C}_{{n}} ^{{k}} \:\:={p}^{'} \left(\mathrm{1}\right)+\mathrm{3}\:{p}^{\left(\mathrm{2}\right)} \left(\mathrm{1}\right)\:+{p}^{\left(\mathrm{3}\right)} \left(\mathrm{1}\right)\: \\ $$$$={n}\:\mathrm{2}^{{n}−\mathrm{1}} \:+\mathrm{3}{n}\left({n}−\mathrm{1}\right)\mathrm{2}^{{n}−\mathrm{2}} \:+{n}\left({n}−\mathrm{1}\right)\left({n}−\mathrm{2}\right)\mathrm{2}^{{n}−\mathrm{3}} \:. \\ $$$$ \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 06/Sep/18
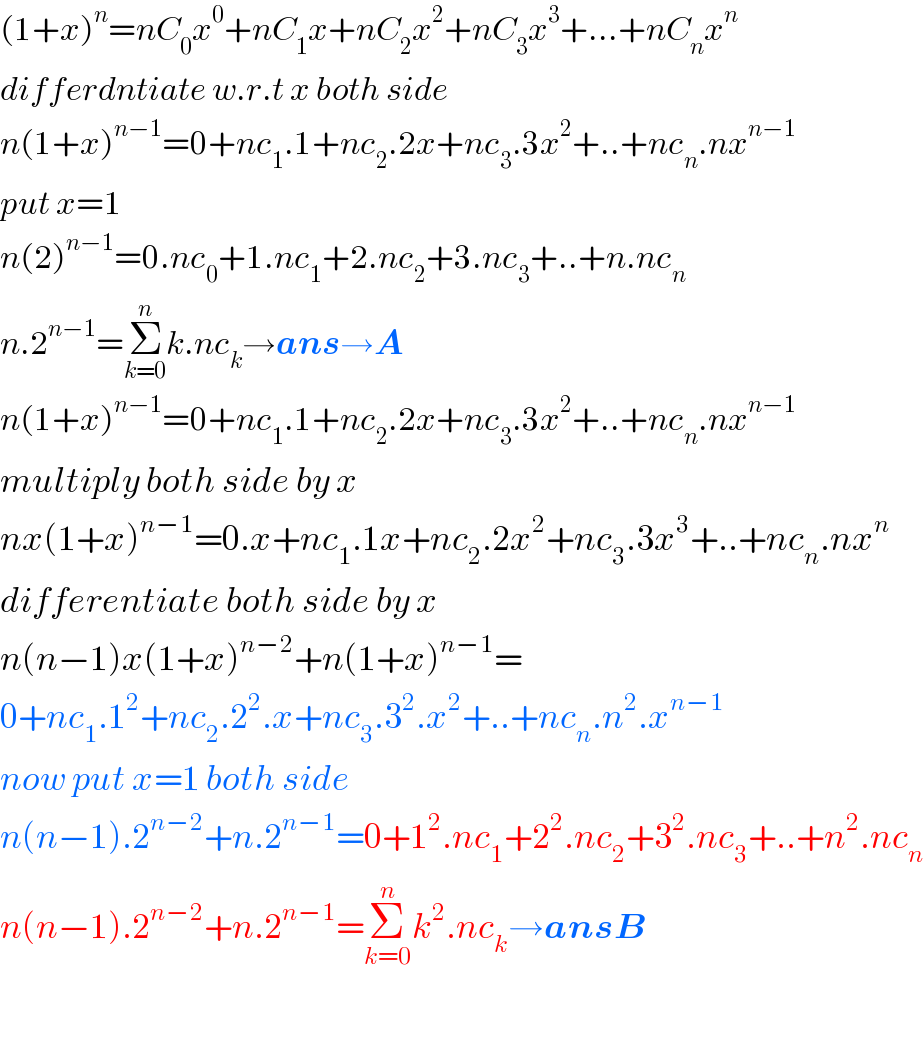
(1+x)^n =nC_0 x^0 +nC_1 x+nC_2 x^2 +nC_3 x^3 +...+nC_n x^n differdntiate w.r.t x both side n(1+x)^(n−1) =0+nc_1 .1+nc_2 .2x+nc_3 .3x^2 +..+nc_n .nx^(n−1) put x=1 n(2)^(n−1) =0.nc_0 +1.nc_1 +2.nc_2 +3.nc_3 +..+n.nc_n n.2^(n−1) =Σ_(k=0) ^n k.nc_k →ans→A n(1+x)^(n−1) =0+nc_1 .1+nc_2 .2x+nc_3 .3x^2 +..+nc_n .nx^(n−1) multiply both side by x nx(1+x)^(n−1) =0.x+nc_1 .1x+nc_2 .2x^2 +nc_3 .3x^3 +..+nc_n .nx^n differentiate both side by x n(n−1)x(1+x)^(n−2) +n(1+x)^(n−1) = 0+nc_1 .1^2 +nc_2 .2^2 .x+nc_3 .3^2 .x^2 +..+nc_n .n^2 .x^(n−1) now put x=1 both side n(n−1).2^(n−2) +n.2^(n−1) =0+1^2 .nc_1 +2^2 .nc_2 +3^2 .nc_3 +..+n^2 .nc_n n(n−1).2^(n−2) +n.2^(n−1) =Σ_(k=0) ^n k^2 .nc_k →ansB
$$\left(\mathrm{1}+{x}\right)^{{n}} ={nC}_{\mathrm{0}} {x}^{\mathrm{0}} +{nC}_{\mathrm{1}} {x}+{nC}_{\mathrm{2}} {x}^{\mathrm{2}} +{nC}_{\mathrm{3}} {x}^{\mathrm{3}} +…+{nC}_{{n}} {x}^{{n}} \\ $$$${differdntiate}\:{w}.{r}.{t}\:{x}\:{both}\:{side} \\ $$$${n}\left(\mathrm{1}+{x}\right)^{{n}−\mathrm{1}} =\mathrm{0}+{nc}_{\mathrm{1}} .\mathrm{1}+{nc}_{\mathrm{2}} .\mathrm{2}{x}+{nc}_{\mathrm{3}} .\mathrm{3}{x}^{\mathrm{2}} +..+{nc}_{{n}} .{nx}^{{n}−\mathrm{1}} \\ $$$${put}\:{x}=\mathrm{1} \\ $$$${n}\left(\mathrm{2}\right)^{{n}−\mathrm{1}} =\mathrm{0}.{nc}_{\mathrm{0}} +\mathrm{1}.{nc}_{\mathrm{1}} +\mathrm{2}.{nc}_{\mathrm{2}} +\mathrm{3}.{nc}_{\mathrm{3}} +..+{n}.{nc}_{{n}} \\ $$$${n}.\mathrm{2}^{{n}−\mathrm{1}} =\underset{{k}=\mathrm{0}} {\overset{{n}} {\sum}}{k}.{nc}_{{k}} \rightarrow\boldsymbol{{ans}}\rightarrow\boldsymbol{{A}} \\ $$$${n}\left(\mathrm{1}+{x}\right)^{{n}−\mathrm{1}} =\mathrm{0}+{nc}_{\mathrm{1}} .\mathrm{1}+{nc}_{\mathrm{2}} .\mathrm{2}{x}+{nc}_{\mathrm{3}} .\mathrm{3}{x}^{\mathrm{2}} +..+{nc}_{{n}} .{nx}^{{n}−\mathrm{1}} \\ $$$${multiply}\:{both}\:{side}\:{by}\:{x} \\ $$$${nx}\left(\mathrm{1}+{x}\right)^{{n}−\mathrm{1}} =\mathrm{0}.{x}+{nc}_{\mathrm{1}} .\mathrm{1}{x}+{nc}_{\mathrm{2}} .\mathrm{2}{x}^{\mathrm{2}} +{nc}_{\mathrm{3}} .\mathrm{3}{x}^{\mathrm{3}} +..+{nc}_{{n}} .{nx}^{{n}} \\ $$$${differentiate}\:{both}\:{side}\:{by}\:{x} \\ $$$${n}\left({n}−\mathrm{1}\right){x}\left(\mathrm{1}+{x}\right)^{{n}−\mathrm{2}} +{n}\left(\mathrm{1}+{x}\right)^{{n}−\mathrm{1}} = \\ $$$$\mathrm{0}+{nc}_{\mathrm{1}} .\mathrm{1}^{\mathrm{2}} +{nc}_{\mathrm{2}} .\mathrm{2}^{\mathrm{2}} .{x}+{nc}_{\mathrm{3}} .\mathrm{3}^{\mathrm{2}} .{x}^{\mathrm{2}} +..+{nc}_{{n}} .{n}^{\mathrm{2}} .{x}^{{n}−\mathrm{1}} \\ $$$${now}\:{put}\:{x}=\mathrm{1}\:{both}\:{side} \\ $$$${n}\left({n}−\mathrm{1}\right).\mathrm{2}^{{n}−\mathrm{2}} +{n}.\mathrm{2}^{{n}−\mathrm{1}} =\mathrm{0}+\mathrm{1}^{\mathrm{2}} .{nc}_{\mathrm{1}} +\mathrm{2}^{\mathrm{2}} .{nc}_{\mathrm{2}} +\mathrm{3}^{\mathrm{2}} .{nc}_{\mathrm{3}} +..+{n}^{\mathrm{2}} .{nc}_{{n}} \\ $$$${n}\left({n}−\mathrm{1}\right).\mathrm{2}^{{n}−\mathrm{2}} +{n}.\mathrm{2}^{{n}−\mathrm{1}} =\underset{{k}=\mathrm{0}} {\overset{{n}} {\sum}}{k}^{\mathrm{2}} .{nc}_{{k}} \rightarrow\boldsymbol{{ansB}} \\ $$$$ \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *