Question Number 64444 by mathmax by abdo last updated on 18/Jul/19
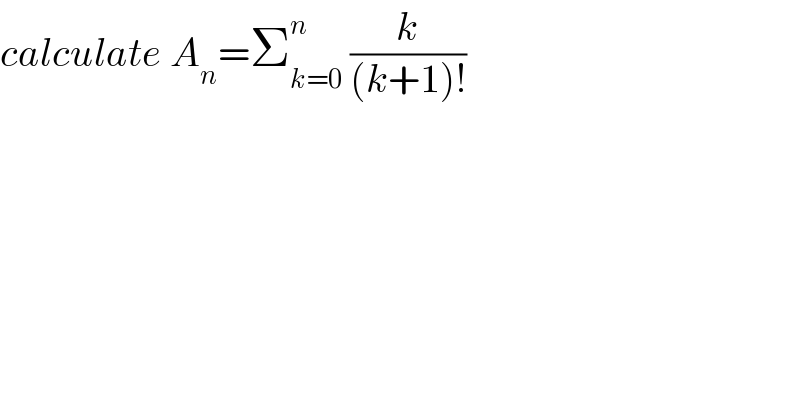
$${calculate}\:{A}_{{n}} =\sum_{{k}=\mathrm{0}} ^{{n}} \:\frac{{k}}{\left({k}+\mathrm{1}\right)!} \\ $$
Commented by Prithwish sen last updated on 18/Jul/19

$$\frac{\mathrm{1}}{\mathrm{k}!}\:−\:\frac{\mathrm{1}}{\left(\mathrm{k}+\mathrm{1}\right)!}\:=\mathrm{1} \\ $$
Commented by mathmax by abdo last updated on 22/Jul/19
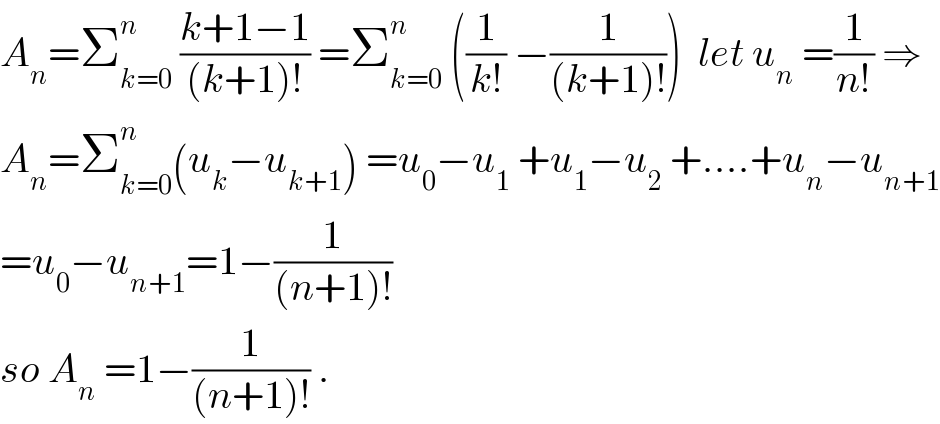
$${A}_{{n}} =\sum_{{k}=\mathrm{0}} ^{{n}} \:\frac{{k}+\mathrm{1}−\mathrm{1}}{\left({k}+\mathrm{1}\right)!}\:=\sum_{{k}=\mathrm{0}} ^{{n}} \:\left(\frac{\mathrm{1}}{{k}!}\:−\frac{\mathrm{1}}{\left({k}+\mathrm{1}\right)!}\right)\:\:{let}\:{u}_{{n}} \:=\frac{\mathrm{1}}{{n}!}\:\Rightarrow \\ $$$${A}_{{n}} =\sum_{{k}=\mathrm{0}} ^{{n}} \left({u}_{{k}} −{u}_{{k}+\mathrm{1}} \right)\:={u}_{\mathrm{0}} −{u}_{\mathrm{1}} \:+{u}_{\mathrm{1}} −{u}_{\mathrm{2}} \:+….+{u}_{{n}} −{u}_{{n}+\mathrm{1}} \\ $$$$={u}_{\mathrm{0}} −{u}_{{n}+\mathrm{1}} =\mathrm{1}−\frac{\mathrm{1}}{\left({n}+\mathrm{1}\right)!} \\ $$$${so}\:{A}_{{n}} \:=\mathrm{1}−\frac{\mathrm{1}}{\left({n}+\mathrm{1}\right)!}\:. \\ $$
