Question Number 39388 by maxmathsup by imad last updated on 05/Jul/18
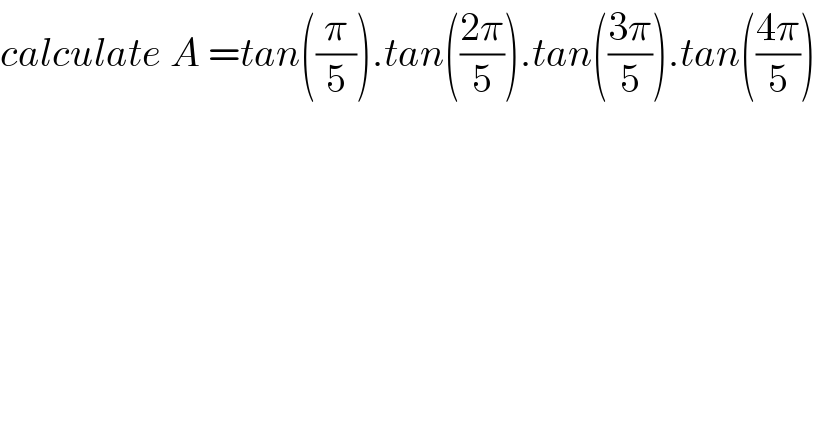
$${calculate}\:{A}\:={tan}\left(\frac{\pi}{\mathrm{5}}\right).{tan}\left(\frac{\mathrm{2}\pi}{\mathrm{5}}\right).{tan}\left(\frac{\mathrm{3}\pi}{\mathrm{5}}\right).{tan}\left(\frac{\mathrm{4}\pi}{\mathrm{5}}\right) \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 06/Jul/18

$${tan}\mathrm{36}.{tan}\mathrm{72}.{tan}\mathrm{108}.{tan}\mathrm{144} \\ $$$${tan}\mathrm{108}={tan}\left(\mathrm{180}−\mathrm{72}\right)=−{tan}\mathrm{72} \\ $$$${tan}\mathrm{144}={tan}\left(\mathrm{180}−\mathrm{36}\right)=−{tan}\mathrm{36} \\ $$$${tan}^{\mathrm{2}} \mathrm{36}×{tan}^{\mathrm{2}} \mathrm{72} \\ $$$$\left({tan}\mathrm{36}.{tan}\mathrm{18}\right)^{\mathrm{2}} \\ $$$$\left(\frac{\frac{\sqrt{\mathrm{10}−\mathrm{2}\sqrt{\mathrm{5}}\:\:}}{\mathrm{4}}}{\frac{\sqrt{\mathrm{5}\:}\:\:+\mathrm{1}}{\mathrm{4}}}×\frac{\frac{\sqrt{\mathrm{5}}\:−\mathrm{1}}{\mathrm{4}}}{\frac{\sqrt{\mathrm{10}+\mathrm{2}\sqrt{\mathrm{5}}\:}}{\mathrm{4}}}\right)^{\mathrm{2}} \\ $$$$=\left(\frac{\mathrm{10}−\mathrm{2}\sqrt{\mathrm{5}\:}}{\mathrm{10}+\mathrm{2}\sqrt{\mathrm{5}}\:}×\frac{\sqrt{\mathrm{5}}\:−\mathrm{1}}{\:\sqrt{\mathrm{5}}\:+\mathrm{1}}\right)^{\mathrm{2}} \\ $$$${devide}\:{N}_{{r}} {andDr}\:{by}\:\mathrm{2}\sqrt{\mathrm{5}}\: \\ $$$$=\left(\left\{\left(\frac{\sqrt{\mathrm{5}}\:−\mathrm{1}}{\:\sqrt{\mathrm{5}}\:+\mathrm{1}}\right)^{\mathrm{2}} \right\}^{\mathrm{2}} =\left(\frac{\mathrm{6}−\mathrm{2}\sqrt{\mathrm{5}}}{\mathrm{6}+\mathrm{2}\sqrt{\mathrm{5}}}\right)^{\mathrm{2}} \:=\left(\frac{\mathrm{3}−\sqrt{\mathrm{5}}\:}{\mathrm{3}+\sqrt{\mathrm{5}}}\right)^{\mathrm{2}} \right. \\ $$$$=\left(\frac{\mathrm{14}−\mathrm{6}\sqrt{\mathrm{5}\:}}{\mathrm{14}+\mathrm{6}\sqrt{\mathrm{5}}}\right) \\ $$
