Menu Close

calculate-arctan-x-1-x-2-dx-

Tinku Tara 0 Comments
Pin




Question Number 48173 by Abdo msup. last updated on 20/Nov/18
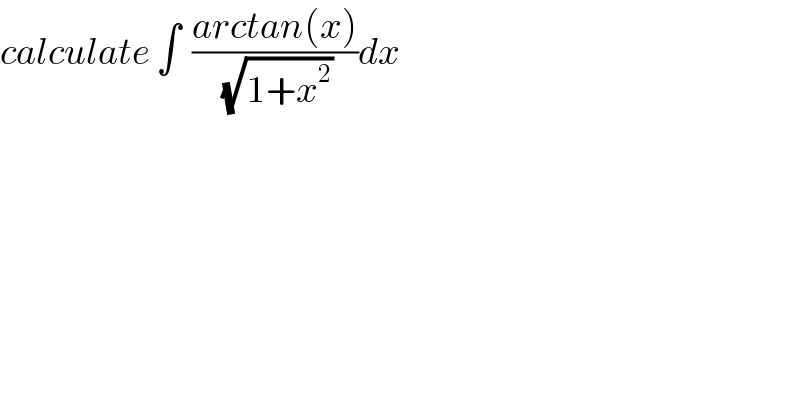
calculate ∫ ((arctan(x))/( (√(1+x^2 ))))dx
$${calculate}\:\int\:\:\frac{{arctan}\left({x}\right)}{\:\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }}{dx} \\ $$
Commented by maxmathsup by imad last updated on 26/Nov/18
changement x=tant give I = ∫ (t/( (√(1+tan^2 t)))) (1+tan^2 t)dθ =∫ θt(√(1+tan^2 t))dt =∫ (t/(cost))dt changement tan((t/2))=u give I = ∫ ((2arctan(u))/((1−u^2 )/(1+u^2 ))) ((2du)/(1+u^2 )) =4 ∫ ((arctan(u))/(1−u^2 )) du let f(α)=∫ ((arctan(αu))/(1−u^2 ))du ⇒f^′ (α) =∫ (u/((1−u^2 )(1+α^2 u^2 )))du =_(αu =x) ∫ (x/(α(1−(x^2 /α^2 ))(1+x^2 ))) (dx/α) =∫ ((xdx)/((α^2 −x^2 )(1+x^2 ))) let decompose F(x) =((−x)/((x^2 −α^2 )(x^2 +1))) ⇒F(x)=(a/(x−α)) +(b/(x+α)) +((cx +d)/(x^2 +1)) we have F(x)=((−x)/((x−α)(x+α)(x^2 +1))) ⇒a=((−α)/(2α(α^2 +1))) =((−1)/(2(α^2 +1))) b =(α/((−2α)(1+α^2 ))) lim_(x→+∞) xF(x) =0 =a+b +c ⇒c=(1/(2(α^2 +1))) +(1/(2(1+α^2 ))) =(1/(1+α^2 )) F(0) =0 =−(a/α) +(b/α) +d ⇒0 =−a+b +αd =(1/(2(α^2 +1))) −(1/(2(1+α^2 ))) +αd ⇒d=0 ⇒ F(x)= ((−1)/(2(1+α^2 )(x−α))) −(1/(2(1+α^2 )(x+α))) +(1/(1+α^2 )) (x/(1+x^2 )) ⇒ ∫ F(x)dx =−(1/(2(1+α^2 )))ln∣x^2 −α^2 ∣ +(1/(2(1+α^2 )))ln(x^2 +1) +c ⇒ f^′ (α) =−(1/(2(1+α^2 )))ln∣α^2 u^2 −α^2 ∣ +(1/(2(1+α^2 )))ln(α^2 u^2 +1) +c ⇒ f(α) =(1/2) ∫_. ^α ((ln∣t^2 u^2 −t^2 ∣)/(1+t^2 ))dt +(1/2) ∫ ((ln(t^2 u^2 +1))/(1+t^2 ))dt +cα +λ ...be continued...
$${changement}\:{x}={tant}\:{give}\:\:{I}\:=\:\int\:\frac{{t}}{\:\sqrt{\mathrm{1}+{tan}^{\mathrm{2}} {t}}}\:\left(\mathrm{1}+{tan}^{\mathrm{2}} {t}\right){d}\theta \\ $$$$=\int\:\theta{t}\sqrt{\mathrm{1}+{tan}^{\mathrm{2}} {t}}{dt}\:=\int\:\:\frac{{t}}{{cost}}{dt}\:{changement}\:{tan}\left(\frac{{t}}{\mathrm{2}}\right)={u}\:{give} \\ $$$${I}\:=\:\int\:\:\frac{\mathrm{2}{arctan}\left({u}\right)}{\frac{\mathrm{1}−{u}^{\mathrm{2}} }{\mathrm{1}+{u}^{\mathrm{2}} }}\:\frac{\mathrm{2}{du}}{\mathrm{1}+{u}^{\mathrm{2}} }\:=\mathrm{4}\:\int\:\:\:\frac{{arctan}\left({u}\right)}{\mathrm{1}−{u}^{\mathrm{2}} }\:{du}\:{let}\: \\ $$$${f}\left(\alpha\right)=\int\:\:\frac{{arctan}\left(\alpha{u}\right)}{\mathrm{1}−{u}^{\mathrm{2}} }{du}\:\Rightarrow{f}^{'} \left(\alpha\right)\:=\int\:\:\frac{{u}}{\left(\mathrm{1}−{u}^{\mathrm{2}} \right)\left(\mathrm{1}+\alpha^{\mathrm{2}} {u}^{\mathrm{2}} \right)}{du} \\ $$$$=_{\alpha{u}\:={x}} \:\:\int\:\:\:\frac{{x}}{\alpha\left(\mathrm{1}−\frac{{x}^{\mathrm{2}} }{\alpha^{\mathrm{2}} }\right)\left(\mathrm{1}+{x}^{\mathrm{2}} \right)}\:\frac{{dx}}{\alpha}\:=\int\:\:\:\frac{{xdx}}{\left(\alpha^{\mathrm{2}} −{x}^{\mathrm{2}} \right)\left(\mathrm{1}+{x}^{\mathrm{2}} \right)}\:{let}\:{decompose} \\ $$$${F}\left({x}\right)\:=\frac{−{x}}{\left({x}^{\mathrm{2}} −\alpha^{\mathrm{2}} \right)\left({x}^{\mathrm{2}} \:+\mathrm{1}\right)}\:\Rightarrow{F}\left({x}\right)=\frac{{a}}{{x}−\alpha}\:+\frac{{b}}{{x}+\alpha}\:+\frac{{cx}\:+{d}}{{x}^{\mathrm{2}} \:+\mathrm{1}}\:{we}\:{have} \\ $$$${F}\left({x}\right)=\frac{−{x}}{\left({x}−\alpha\right)\left({x}+\alpha\right)\left({x}^{\mathrm{2}} \:+\mathrm{1}\right)}\:\Rightarrow{a}=\frac{−\alpha}{\mathrm{2}\alpha\left(\alpha^{\mathrm{2}} \:+\mathrm{1}\right)}\:=\frac{−\mathrm{1}}{\mathrm{2}\left(\alpha^{\mathrm{2}} \:+\mathrm{1}\right)} \\ $$$${b}\:=\frac{\alpha}{\left(−\mathrm{2}\alpha\right)\left(\mathrm{1}+\alpha^{\mathrm{2}} \right)} \\ $$$${lim}_{{x}\rightarrow+\infty} {xF}\left({x}\right)\:=\mathrm{0}\:={a}+{b}\:+{c}\:\Rightarrow{c}=\frac{\mathrm{1}}{\mathrm{2}\left(\alpha^{\mathrm{2}} \:+\mathrm{1}\right)}\:+\frac{\mathrm{1}}{\mathrm{2}\left(\mathrm{1}+\alpha^{\mathrm{2}} \right)}\:=\frac{\mathrm{1}}{\mathrm{1}+\alpha^{\mathrm{2}} } \\ $$$${F}\left(\mathrm{0}\right)\:=\mathrm{0}\:=−\frac{{a}}{\alpha}\:+\frac{{b}}{\alpha}\:+{d}\:\Rightarrow\mathrm{0}\:=−{a}+{b}\:+\alpha{d}\:=\frac{\mathrm{1}}{\mathrm{2}\left(\alpha^{\mathrm{2}} \:+\mathrm{1}\right)}\:−\frac{\mathrm{1}}{\mathrm{2}\left(\mathrm{1}+\alpha^{\mathrm{2}} \right)}\:+\alpha{d}\:\Rightarrow{d}=\mathrm{0}\:\Rightarrow \\ $$$${F}\left({x}\right)=\:\frac{−\mathrm{1}}{\mathrm{2}\left(\mathrm{1}+\alpha^{\mathrm{2}} \right)\left({x}−\alpha\right)}\:−\frac{\mathrm{1}}{\mathrm{2}\left(\mathrm{1}+\alpha^{\mathrm{2}} \right)\left({x}+\alpha\right)}\:+\frac{\mathrm{1}}{\mathrm{1}+\alpha^{\mathrm{2}} }\:\frac{{x}}{\mathrm{1}+{x}^{\mathrm{2}} }\:\Rightarrow \\ $$$$\int\:{F}\left({x}\right){dx}\:=−\frac{\mathrm{1}}{\mathrm{2}\left(\mathrm{1}+\alpha^{\mathrm{2}} \right)}{ln}\mid{x}^{\mathrm{2}} \:−\alpha^{\mathrm{2}} \mid\:+\frac{\mathrm{1}}{\mathrm{2}\left(\mathrm{1}+\alpha^{\mathrm{2}} \right)}{ln}\left({x}^{\mathrm{2}} \:+\mathrm{1}\right)\:+{c}\:\Rightarrow \\ $$$${f}^{'} \left(\alpha\right)\:=−\frac{\mathrm{1}}{\mathrm{2}\left(\mathrm{1}+\alpha^{\mathrm{2}} \right)}{ln}\mid\alpha^{\mathrm{2}} {u}^{\mathrm{2}} −\alpha^{\mathrm{2}} \mid\:+\frac{\mathrm{1}}{\mathrm{2}\left(\mathrm{1}+\alpha^{\mathrm{2}} \right)}{ln}\left(\alpha^{\mathrm{2}} {u}^{\mathrm{2}} \:+\mathrm{1}\right)\:+{c}\:\:\Rightarrow \\ $$$${f}\left(\alpha\right)\:=\frac{\mathrm{1}}{\mathrm{2}}\:\int_{.} ^{\alpha} \:\:\frac{{ln}\mid{t}^{\mathrm{2}} {u}^{\mathrm{2}} −{t}^{\mathrm{2}} \mid}{\mathrm{1}+{t}^{\mathrm{2}} }{dt}\:+\frac{\mathrm{1}}{\mathrm{2}}\:\int\:\frac{{ln}\left({t}^{\mathrm{2}} {u}^{\mathrm{2}} \:+\mathrm{1}\right)}{\mathrm{1}+{t}^{\mathrm{2}} }{dt}\:+{c}\alpha\:+\lambda\:\:…{be}\:{continued}… \\ $$
Commented by maxmathsup by imad last updated on 26/Nov/18
let find I at form of serie we have I =∫ (t/(cost))dt I =∫ (t/((e^(it) +e^(−it) )/2)) dt =∫ ((2t)/(e^(it) +e^(−it) )) dt = ∫ ((2t e^(−it) )/(1+e^(−2it) )) dt =2 ∫ t e^(−it) (Σ_(n=0) ^∞ (−1)^n e^(−2int) )dt= 2Σ_(n=0) ^∞ (−1)^n ∫ t e^(−(2n+1)it) dt =2 Σ_(n=0) ^∞ (−1)^n A_n by parts A_n =−(1/((2n+1)i)) t e^(−(2n+1)it) −∫ −(1/((2n+1)i)) e^(−(2n+1)it) dt =((it)/(2n+1)) e^(−(2n+1)it) −(i/(2n+1)) (−(1/((2n+1)i))) e^(−(2n+1)it) =((it)/(2n+1)) e^(−(2n+1)it) +(1/((2n+1)^2 )) e^(−(2n+1)it) ⇒ Σ_(n=0) ^∞ A_n =it Σ_(n=0) ^∞ (e^(−(2n+1)it) /(2n+1)) +Σ_(n=0) ^∞ (e^(−(2n+1)it) /((2n+1)^2 )) ....be continued...
$${let}\:{find}\:{I}\:{at}\:{form}\:{of}\:{serie}\:{we}\:{have}\:{I}\:=\int\:\:\frac{{t}}{{cost}}{dt} \\ $$$${I}\:=\int\:\:\frac{{t}}{\frac{{e}^{{it}} \:+{e}^{−{it}} }{\mathrm{2}}}\:{dt}\:=\int\:\:\frac{\mathrm{2}{t}}{{e}^{{it}} \:+{e}^{−{it}} }\:{dt}\:=\:\int\:\frac{\mathrm{2}{t}\:{e}^{−{it}} }{\mathrm{1}+{e}^{−\mathrm{2}{it}} }\:{dt} \\ $$$$=\mathrm{2}\:\int\:\:\:{t}\:{e}^{−{it}} \:\left(\sum_{{n}=\mathrm{0}} ^{\infty} \left(−\mathrm{1}\right)^{{n}} \:{e}^{−\mathrm{2}{int}} \right){dt}=\:\mathrm{2}\sum_{{n}=\mathrm{0}} ^{\infty} \:\left(−\mathrm{1}\right)^{{n}} \:\int\:{t}\:{e}^{−\left(\mathrm{2}{n}+\mathrm{1}\right){it}} {dt} \\ $$$$=\mathrm{2}\:\sum_{{n}=\mathrm{0}} ^{\infty} \:\left(−\mathrm{1}\right)^{{n}} \:{A}_{{n}} \:\:\:{by}\:{parts}\:{A}_{{n}} =−\frac{\mathrm{1}}{\left(\mathrm{2}{n}+\mathrm{1}\right){i}}\:{t}\:{e}^{−\left(\mathrm{2}{n}+\mathrm{1}\right){it}} \:−\int\:−\frac{\mathrm{1}}{\left(\mathrm{2}{n}+\mathrm{1}\right){i}}\:{e}^{−\left(\mathrm{2}{n}+\mathrm{1}\right){it}} {dt} \\ $$$$=\frac{{it}}{\mathrm{2}{n}+\mathrm{1}}\:{e}^{−\left(\mathrm{2}{n}+\mathrm{1}\right){it}} \:−\frac{{i}}{\mathrm{2}{n}+\mathrm{1}}\:\left(−\frac{\mathrm{1}}{\left(\mathrm{2}{n}+\mathrm{1}\right){i}}\right)\:{e}^{−\left(\mathrm{2}{n}+\mathrm{1}\right){it}} \\ $$$$=\frac{{it}}{\mathrm{2}{n}+\mathrm{1}}\:{e}^{−\left(\mathrm{2}{n}+\mathrm{1}\right){it}} \:+\frac{\mathrm{1}}{\left(\mathrm{2}{n}+\mathrm{1}\right)^{\mathrm{2}} }\:{e}^{−\left(\mathrm{2}{n}+\mathrm{1}\right){it}} \:\Rightarrow \\ $$$$\sum_{{n}=\mathrm{0}} ^{\infty} \:{A}_{{n}} ={it}\:\sum_{{n}=\mathrm{0}} ^{\infty} \:\:\:\frac{{e}^{−\left(\mathrm{2}{n}+\mathrm{1}\right){it}} }{\mathrm{2}{n}+\mathrm{1}}\:+\sum_{{n}=\mathrm{0}} ^{\infty} \:\:\frac{{e}^{−\left(\mathrm{2}{n}+\mathrm{1}\right){it}} }{\left(\mathrm{2}{n}+\mathrm{1}\right)^{\mathrm{2}} }\:….{be}\:{continued}… \\ $$
Answered by Abdulhafeez Abu qatada last updated on 21/Nov/18

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *