Question Number 50397 by Abdo msup. last updated on 16/Dec/18

$${calculate}\:{artan}\left(\mathrm{2}\right)+{arctan}\left(\mathrm{5}\right)+{arctan}\left(\mathrm{8}\right) \\ $$
Answered by mr W last updated on 17/Dec/18
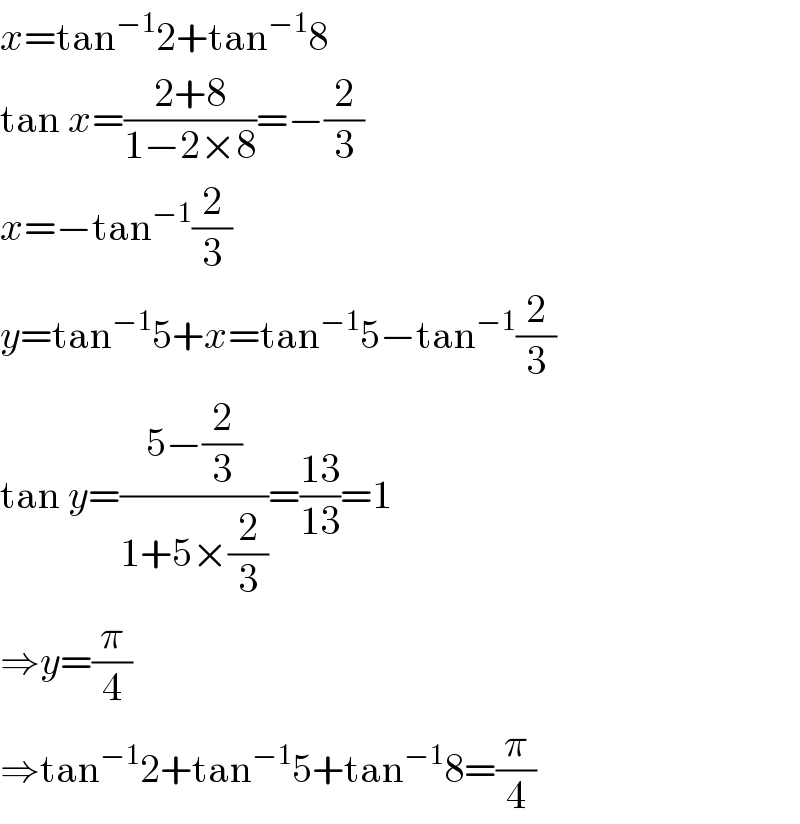
$${x}=\mathrm{tan}^{−\mathrm{1}} \mathrm{2}+\mathrm{tan}^{−\mathrm{1}} \mathrm{8} \\ $$$$\mathrm{tan}\:{x}=\frac{\mathrm{2}+\mathrm{8}}{\mathrm{1}−\mathrm{2}×\mathrm{8}}=−\frac{\mathrm{2}}{\mathrm{3}} \\ $$$${x}=−\mathrm{tan}^{−\mathrm{1}} \frac{\mathrm{2}}{\mathrm{3}} \\ $$$${y}=\mathrm{tan}^{−\mathrm{1}} \mathrm{5}+{x}=\mathrm{tan}^{−\mathrm{1}} \mathrm{5}−\mathrm{tan}^{−\mathrm{1}} \frac{\mathrm{2}}{\mathrm{3}} \\ $$$$\mathrm{tan}\:{y}=\frac{\mathrm{5}−\frac{\mathrm{2}}{\mathrm{3}}}{\mathrm{1}+\mathrm{5}×\frac{\mathrm{2}}{\mathrm{3}}}=\frac{\mathrm{13}}{\mathrm{13}}=\mathrm{1} \\ $$$$\Rightarrow{y}=\frac{\pi}{\mathrm{4}} \\ $$$$\Rightarrow\mathrm{tan}^{−\mathrm{1}} \mathrm{2}+\mathrm{tan}^{−\mathrm{1}} \mathrm{5}+\mathrm{tan}^{−\mathrm{1}} \mathrm{8}=\frac{\pi}{\mathrm{4}} \\ $$
