Menu Close

calculate-B-n-k-0-n-1-k-2k-2-1-interms-of-n-

Tinku Tara 0 Comments
Pin




Question Number 37891 by abdo mathsup 649 cc last updated on 19/Jun/18
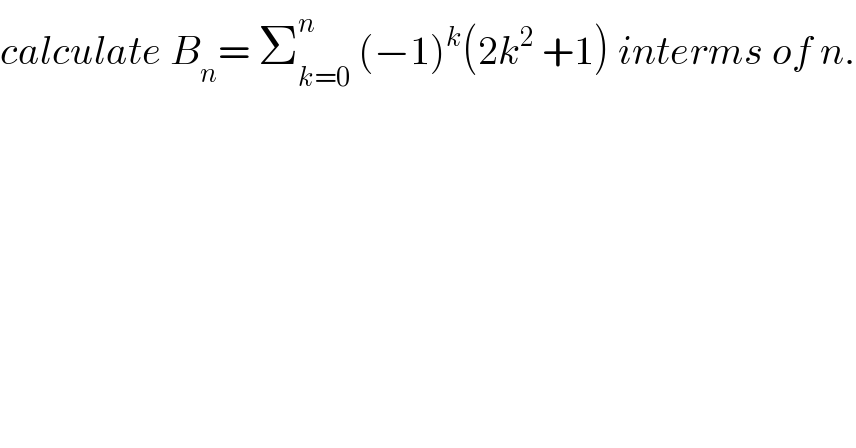
calculate B_n = Σ_(k=0) ^n (−1)^k (2k^2 +1) interms of n.
$${calculate}\:{B}_{{n}} =\:\sum_{{k}=\mathrm{0}} ^{{n}} \:\left(−\mathrm{1}\right)^{{k}} \left(\mathrm{2}{k}^{\mathrm{2}} \:+\mathrm{1}\right)\:{interms}\:{of}\:{n}. \\ $$
Commented by prof Abdo imad last updated on 24/Jun/18
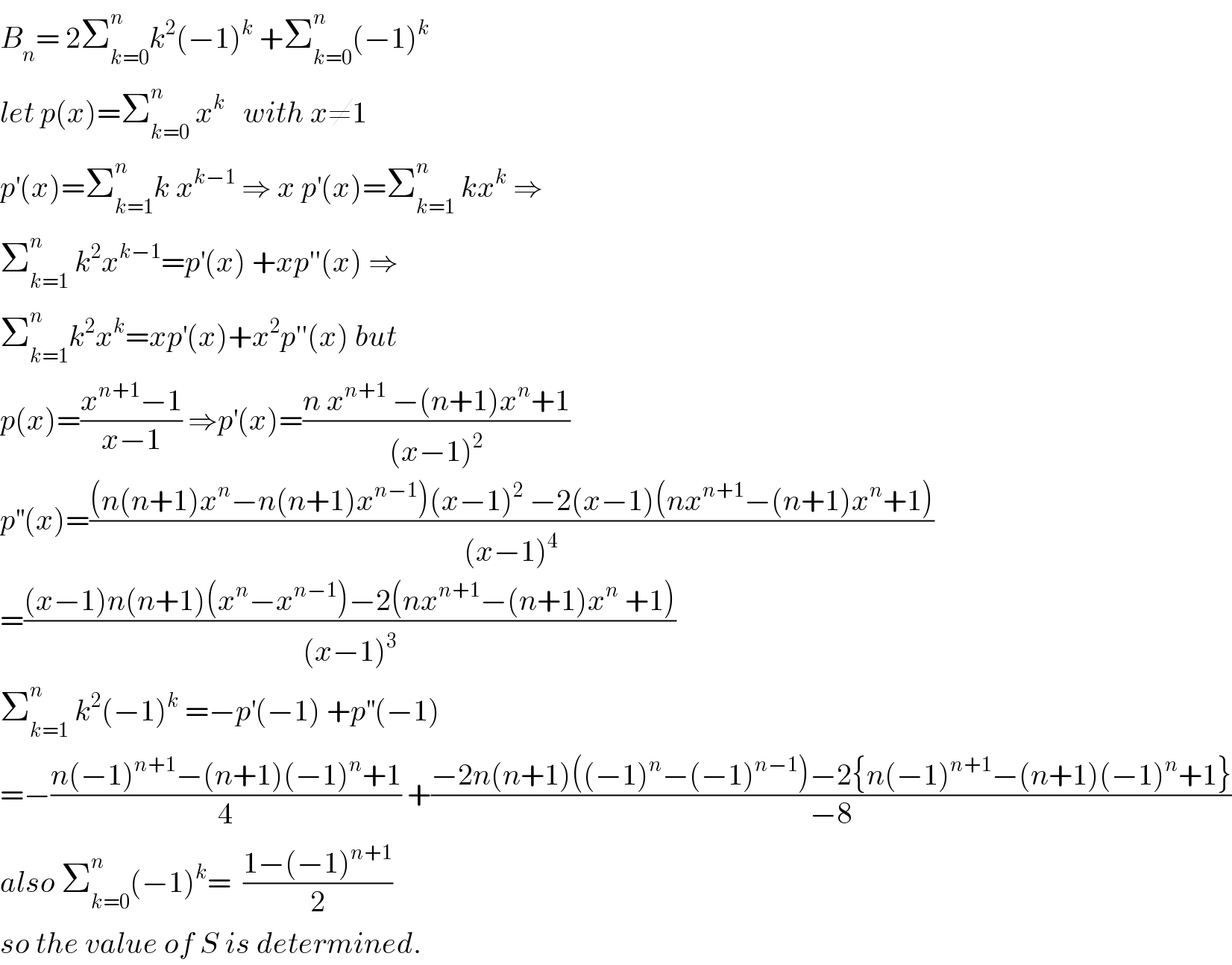
B_n = 2Σ_(k=0) ^n k^2 (−1)^k +Σ_(k=0) ^n (−1)^k let p(x)=Σ_(k=0) ^n x^k with x≠1 p^′ (x)=Σ_(k=1) ^n k x^(k−1) ⇒ x p^′ (x)=Σ_(k=1) ^n kx^k ⇒ Σ_(k=1) ^n k^2 x^(k−1) =p^′ (x) +xp′′(x) ⇒ Σ_(k=1) ^n k^2 x^k =xp^′ (x)+x^2 p′′(x) but p(x)=((x^(n+1) −1)/(x−1)) ⇒p^′ (x)=((n x^(n+1) −(n+1)x^n +1)/((x−1)^2 )) p^(′′) (x)=(((n(n+1)x^n −n(n+1)x^(n−1) )(x−1)^2 −2(x−1)(nx^(n+1) −(n+1)x^n +1))/((x−1)^4 )) =(((x−1)n(n+1)(x^n −x^(n−1) )−2(nx^(n+1) −(n+1)x^n +1))/((x−1)^3 )) Σ_(k=1) ^n k^2 (−1)^k =−p^′ (−1) +p^(′′) (−1) =−((n(−1)^(n+1) −(n+1)(−1)^n +1)/4) +((−2n(n+1)((−1)^n −(−1)^(n−1) )−2{n(−1)^(n+1) −(n+1)(−1)^n +1})/(−8)) also Σ_(k=0) ^n (−1)^k = ((1−(−1)^(n+1) )/2) so the value of S is determined.
$${B}_{{n}} =\:\mathrm{2}\sum_{{k}=\mathrm{0}} ^{{n}} {k}^{\mathrm{2}} \left(−\mathrm{1}\right)^{{k}} \:+\sum_{{k}=\mathrm{0}} ^{{n}} \left(−\mathrm{1}\right)^{{k}} \\ $$$${let}\:{p}\left({x}\right)=\sum_{{k}=\mathrm{0}} ^{{n}} \:{x}^{{k}} \:\:\:{with}\:{x}\neq\mathrm{1} \\ $$$${p}^{'} \left({x}\right)=\sum_{{k}=\mathrm{1}} ^{{n}} {k}\:{x}^{{k}−\mathrm{1}} \:\Rightarrow\:{x}\:{p}^{'} \left({x}\right)=\sum_{{k}=\mathrm{1}} ^{{n}} \:{kx}^{{k}} \:\Rightarrow \\ $$$$\sum_{{k}=\mathrm{1}} ^{{n}} \:{k}^{\mathrm{2}} {x}^{{k}−\mathrm{1}} ={p}^{'} \left({x}\right)\:+{xp}''\left({x}\right)\:\Rightarrow \\ $$$$\sum_{{k}=\mathrm{1}} ^{{n}} {k}^{\mathrm{2}} {x}^{{k}} ={xp}^{'} \left({x}\right)+{x}^{\mathrm{2}} {p}''\left({x}\right)\:{but} \\ $$$${p}\left({x}\right)=\frac{{x}^{{n}+\mathrm{1}} −\mathrm{1}}{{x}−\mathrm{1}}\:\Rightarrow{p}^{'} \left({x}\right)=\frac{{n}\:{x}^{{n}+\mathrm{1}} \:−\left({n}+\mathrm{1}\right){x}^{{n}} +\mathrm{1}}{\left({x}−\mathrm{1}\right)^{\mathrm{2}} } \\ $$$${p}^{''} \left({x}\right)=\frac{\left({n}\left({n}+\mathrm{1}\right){x}^{{n}} −{n}\left({n}+\mathrm{1}\right){x}^{{n}−\mathrm{1}} \right)\left({x}−\mathrm{1}\right)^{\mathrm{2}} \:−\mathrm{2}\left({x}−\mathrm{1}\right)\left({nx}^{{n}+\mathrm{1}} −\left({n}+\mathrm{1}\right){x}^{{n}} +\mathrm{1}\right)}{\left({x}−\mathrm{1}\right)^{\mathrm{4}} } \\ $$$$=\frac{\left({x}−\mathrm{1}\right){n}\left({n}+\mathrm{1}\right)\left({x}^{{n}} −{x}^{{n}−\mathrm{1}} \right)−\mathrm{2}\left({nx}^{{n}+\mathrm{1}} −\left({n}+\mathrm{1}\right){x}^{{n}} \:+\mathrm{1}\right)}{\left({x}−\mathrm{1}\right)^{\mathrm{3}} } \\ $$$$\sum_{{k}=\mathrm{1}} ^{{n}} \:{k}^{\mathrm{2}} \left(−\mathrm{1}\right)^{{k}} \:=−{p}^{'} \left(−\mathrm{1}\right)\:+{p}^{''} \left(−\mathrm{1}\right) \\ $$$$=−\frac{{n}\left(−\mathrm{1}\right)^{{n}+\mathrm{1}} −\left({n}+\mathrm{1}\right)\left(−\mathrm{1}\right)^{{n}} +\mathrm{1}}{\mathrm{4}}\:+\frac{−\mathrm{2}{n}\left({n}+\mathrm{1}\right)\left(\left(−\mathrm{1}\right)^{{n}} −\left(−\mathrm{1}\right)^{{n}−\mathrm{1}} \right)−\mathrm{2}\left\{{n}\left(−\mathrm{1}\right)^{{n}+\mathrm{1}} −\left({n}+\mathrm{1}\right)\left(−\mathrm{1}\right)^{{n}} +\mathrm{1}\right\}}{−\mathrm{8}} \\ $$$${also}\:\sum_{{k}=\mathrm{0}} ^{{n}} \left(−\mathrm{1}\right)^{{k}} =\:\:\frac{\mathrm{1}−\left(−\mathrm{1}\right)^{{n}+\mathrm{1}} }{\mathrm{2}} \\ $$$${so}\:{the}\:{value}\:{of}\:{S}\:{is}\:{determined}. \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *