Question Number 87306 by abdomathmax last updated on 03/Apr/20

Commented by Ar Brandon last updated on 03/Apr/20
![My suggestion ∫_1 ^(+∞) (x/(x^4 +1))dx=∫_1 ^(+∞) (x/(1+(x^2 )^2 ))dx=(1/2)∫_1 ^(+∞) ((2x)/(1+(x^2 )^2 ))dx =(1/2)[arctan(x^2 )]_1 ^(+∞) =(1/2)((π/2))−(1/2)((π/4))=(π/8)](https://www.tinkutara.com/question/Q87320.png)
Commented by Ar Brandon last updated on 04/Apr/20
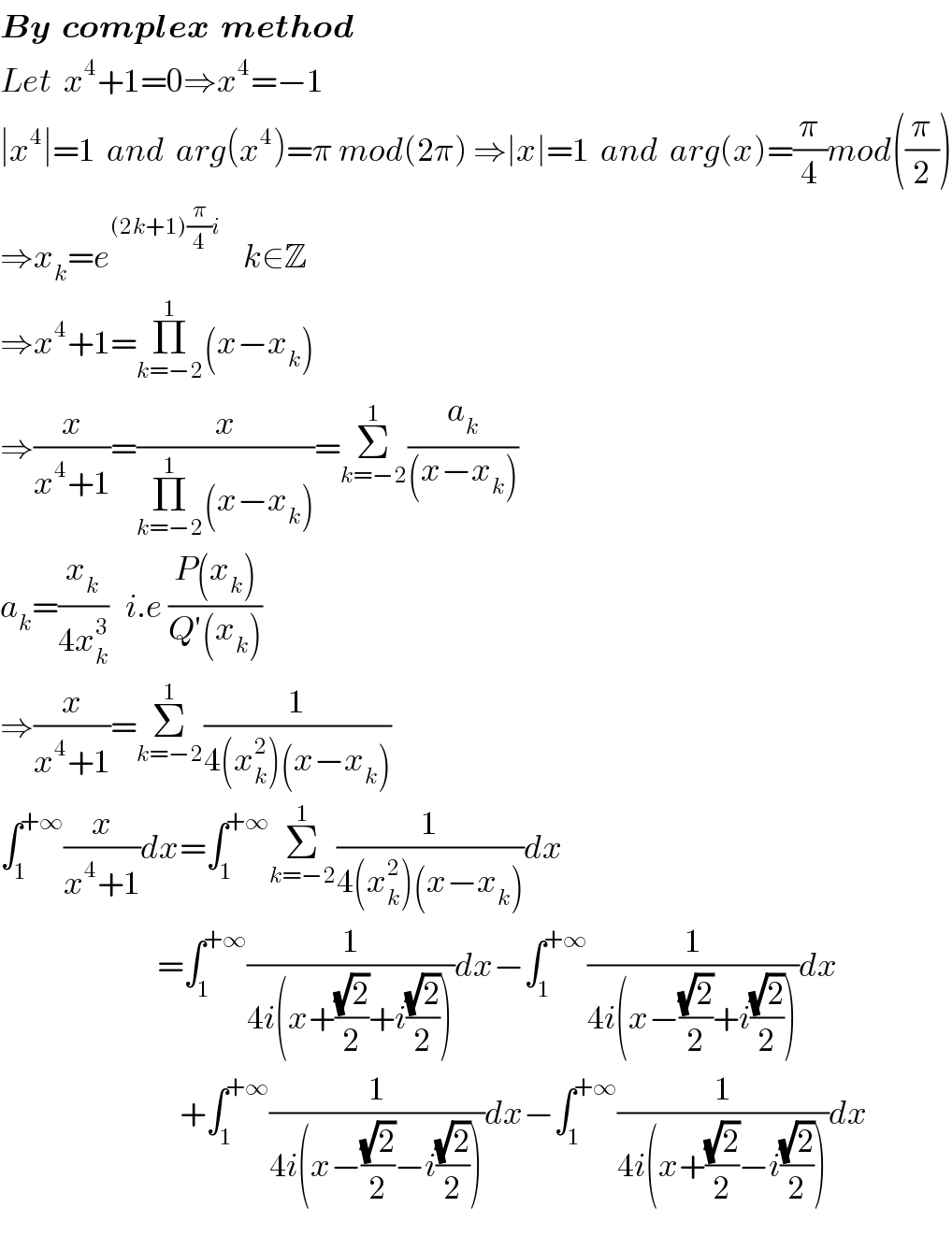
Commented by Ar Brandon last updated on 04/Apr/20

Commented by mathmax by abdo last updated on 04/Apr/20

Commented by mathmax by abdo last updated on 04/Apr/20
![let decompose F(x)=(x/(x^4 +1)) poles of F? x^4 +1 =0 ⇔ x^4 =e^((2k+1)π) ⇒ x_k =e^((i(2k+1)π)/4) and k∈[[0,3]] F(x) =Σ_(k.=0) ^3 (a_k /(x−x_k )) with a_(k ) =(x_k /(4x_k ^3 )) =−(1/4)x_k ^2 =−(1/4)e^((i(2k+1)π)/2) =−(1/4) (i)^(2k+1) =−(1/4)(−1)^k i =(i/4)(−1)^k ⇒ ∫_1 ^(+∞) F(x)dx =(i/4) Σ_(k=0) ^3 (−1)^k ∫_1 ^(+∞) (dx/(x−x_k )) we have x_0 =e^((iπ)/4) , x_1 =e^((i3π)/4) , x_2 =e^(i((5π)/4)) =x_1 ^− , x_3 =e^((i7π)/4) =e^(i(((8π−π)/4))) =x_0 ^− ⇒ ∫_1 ^(+∞) F(x)dx =(i/4){ ∫_1 ^(+∞) (dx/(x−x_0 ))−∫_1 ^(+∞) (dx/(x−x_1 )) +∫_1 ^(+∞) (dx/(x−x_1 ^− )) −∫_1 ^(+∞) (dx/(x−x_0 ^− ))} =(i/4)[ln(((x−x_o )/(x−x_1 )))]_1 ^(+∞) +[ln(((x−x_1 ^− )/(x−x_0 ^− )))]_1 ^(+∞) =(i/4)(−ln(((1−x_0 )/(1−x_1 )))−ln(((1−x_1 ^− )/(1−x_0 ^− )))) =(i/4){ ln(((1−x_1 )/(1−x_0 )))+ln(((1−x_0 ^− )/(1−x_1 ^− )))} rest to finish the calculus](https://www.tinkutara.com/question/Q87460.png)
Commented by Ar Brandon last updated on 04/Apr/20

Commented by Ar Brandon last updated on 04/Apr/20
��
Commented by mind is power last updated on 04/Apr/20

Commented by Ar Brandon last updated on 05/Apr/20

Answered by mind is power last updated on 04/Apr/20
![∫_0 ^1 ((xdx)/((x^4 +1)))=∫_1 ^(+∞) ((xdx)/((1+x^4 ))) ∫_1 ^(+∞) ((xdx)/(x^4 +1))=(1/2)∫_0 ^∞ ((xdx)/(x^4 +1)) f(z)=(z/(1+z^4 )),let C_R =[0,R]∪{Re^(iθ) ,θ∈[0,(π/2)]}_(=γ) ∪[iR,0];R>1 ∫_C_R f(z)dz=2iπRes(f,z=e^(i(π/4)) )=2iπ.(1/(4(e^(i(π/2)) )))=(π/2) ∫_γ f(z)dz=∫_0 ^(π/2) Rie^(iθ) f(Re^(iθ) )dθ =iR^2 ∫_0 ^(π/2) (e^(2iθ) /(R^4 e^(4iθ) +1))dθ,∣∫f(z)dz∣≤(π/2).(R^2 /(R^4 −1))→0 as R→∞ ∫_(iR) ^0 f(z)dz=i∫_R ^0 f(it)dz=∫_0 ^R (t/(t^4 +1))dt ⇒lim_(R→∞) ∫_C_R f(z)dz=lim_(R→∞) 2∫_0 ^R ((tdt)/(t^4 +1))=(π/2) ∫_0 ^∞ ((tdt)/(t^4 +1)).=(π/4) ∫_1 ^∞ ((xdx)/(x^4 +1))=(π/8) .](https://www.tinkutara.com/question/Q87331.png)
Commented by mathmax by abdo last updated on 04/Apr/20

Commented by mind is power last updated on 04/Apr/20

