Question Number 33362 by prof Abdo imad last updated on 15/Apr/18
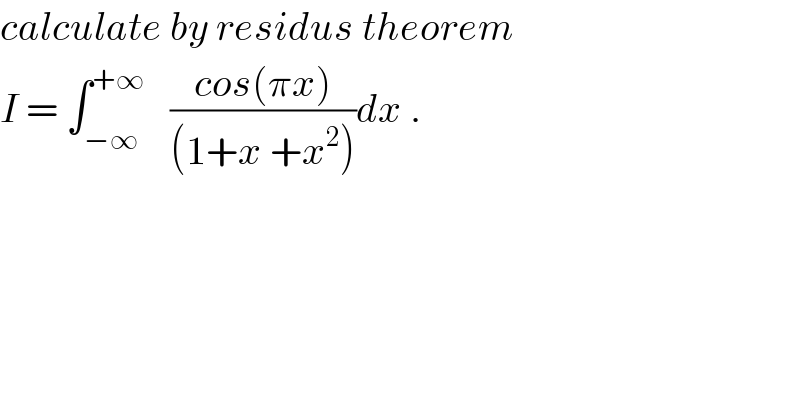
$${calculate}\:{by}\:{residus}\:{theorem} \\ $$$${I}\:=\:\int_{−\infty} ^{+\infty} \:\:\:\frac{{cos}\left(\pi{x}\right)}{\left(\mathrm{1}+{x}\:+{x}^{\mathrm{2}} \right)}{dx}\:. \\ $$
Commented by prof Abdo imad last updated on 15/Apr/18
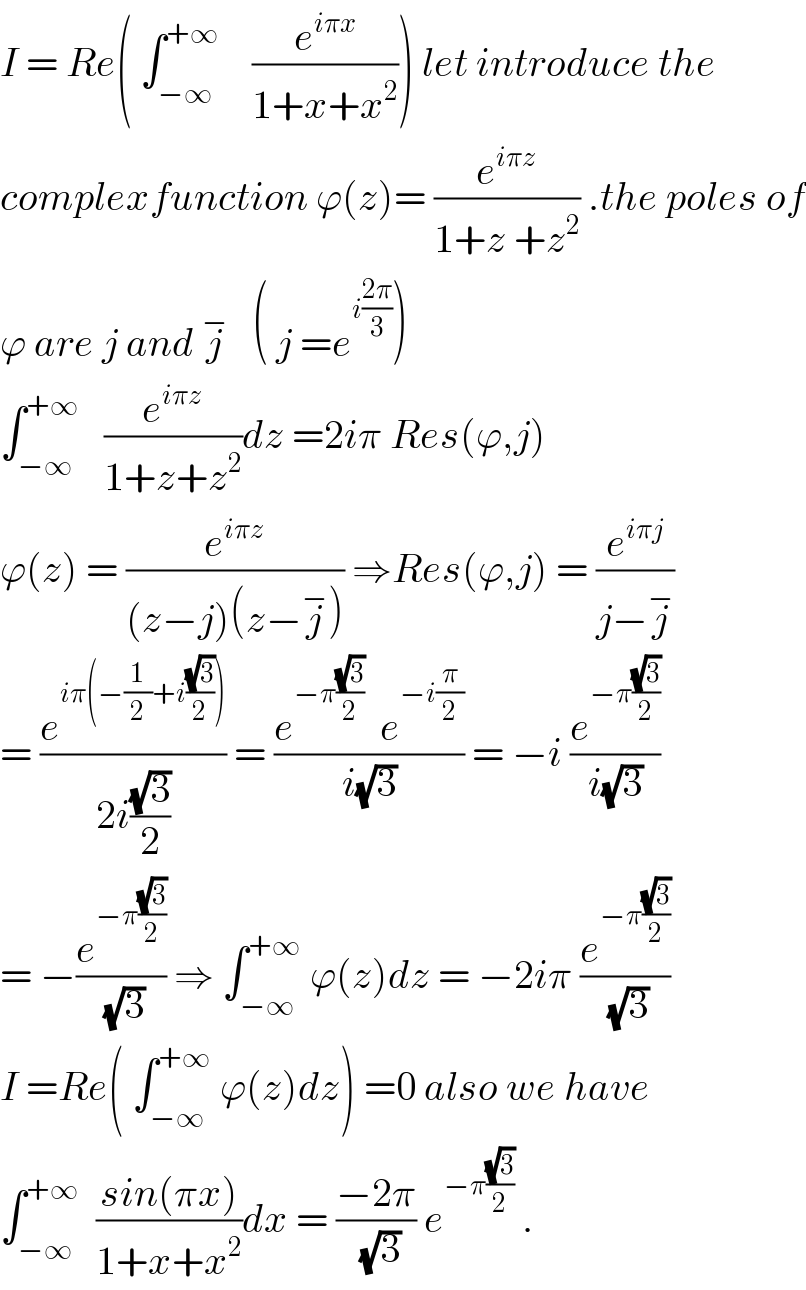
$${I}\:=\:{Re}\left(\:\int_{−\infty} ^{+\infty} \:\:\:\:\frac{{e}^{{i}\pi{x}} }{\mathrm{1}+{x}+{x}^{\mathrm{2}} }\right)\:{let}\:{introduce}\:{the} \\ $$$${complexfunction}\:\varphi\left({z}\right)=\:\frac{{e}^{{i}\pi{z}} }{\mathrm{1}+{z}\:+{z}^{\mathrm{2}} }\:.{the}\:{poles}\:{of} \\ $$$$\varphi\:{are}\:{j}\:{and}\:\overset{−} {{j}}\:\:\:\left(\:{j}\:={e}^{{i}\frac{\mathrm{2}\pi}{\mathrm{3}}} \right) \\ $$$$\int_{−\infty} ^{+\infty} \:\:\:\frac{{e}^{{i}\pi{z}} }{\mathrm{1}+{z}+{z}^{\mathrm{2}} }{dz}\:=\mathrm{2}{i}\pi\:{Res}\left(\varphi,{j}\right) \\ $$$$\varphi\left({z}\right)\:=\:\frac{{e}^{{i}\pi{z}} }{\left({z}−{j}\right)\left({z}−\overset{−} {{j}}\right)}\:\Rightarrow{Res}\left(\varphi,{j}\right)\:=\:\frac{{e}^{{i}\pi{j}} }{{j}−\overset{−} {{j}}} \\ $$$$=\:\frac{{e}^{{i}\pi\left(−\frac{\mathrm{1}}{\mathrm{2}}+{i}\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\right)} }{\mathrm{2}{i}\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}}\:=\:\frac{{e}^{−\pi\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}} \:\:{e}^{−{i}\frac{\pi}{\mathrm{2}}} }{{i}\sqrt{\mathrm{3}}}\:=\:−{i}\:\frac{{e}^{−\pi\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}} }{{i}\sqrt{\mathrm{3}}} \\ $$$$=\:−\frac{{e}^{−\pi\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}} }{\:\sqrt{\mathrm{3}}}\:\Rightarrow\:\int_{−\infty} ^{+\infty} \:\varphi\left({z}\right){dz}\:=\:−\mathrm{2}{i}\pi\:\frac{{e}^{−\pi\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}} }{\:\sqrt{\mathrm{3}}} \\ $$$${I}\:={Re}\left(\:\int_{−\infty} ^{+\infty} \:\varphi\left({z}\right){dz}\right)\:=\mathrm{0}\:{also}\:{we}\:{have} \\ $$$$\int_{−\infty} ^{+\infty} \:\:\frac{{sin}\left(\pi{x}\right)}{\mathrm{1}+{x}+{x}^{\mathrm{2}} }{dx}\:=\:\frac{−\mathrm{2}\pi}{\:\sqrt{\mathrm{3}}}\:{e}^{−\pi\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}} \:. \\ $$
