Question Number 101522 by bramlex last updated on 03/Jul/20
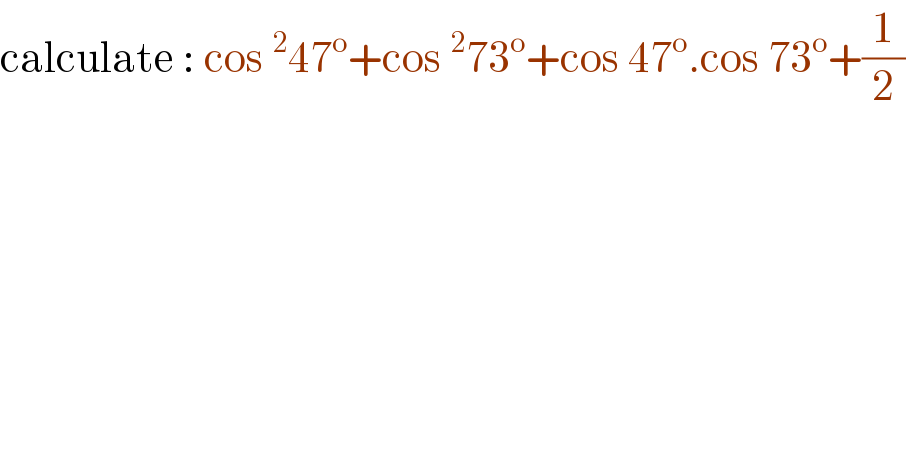
$$\mathrm{calculate}\::\:\mathrm{cos}\:^{\mathrm{2}} \mathrm{47}^{\mathrm{o}} +\mathrm{cos}\:^{\mathrm{2}} \mathrm{73}^{\mathrm{o}} +\mathrm{cos}\:\mathrm{47}^{\mathrm{o}} .\mathrm{cos}\:\mathrm{73}^{\mathrm{o}} +\frac{\mathrm{1}}{\mathrm{2}} \\ $$
Commented by bemath last updated on 03/Jul/20
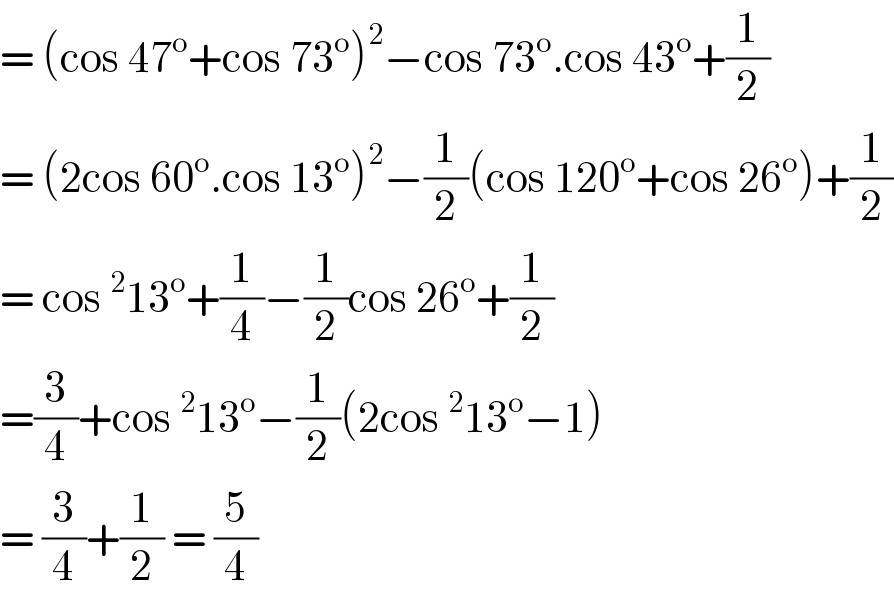
$$=\:\left(\mathrm{cos}\:\mathrm{47}^{\mathrm{o}} +\mathrm{cos}\:\mathrm{73}^{\mathrm{o}} \right)^{\mathrm{2}} −\mathrm{cos}\:\mathrm{73}^{\mathrm{o}} .\mathrm{cos}\:\mathrm{43}^{\mathrm{o}} +\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$=\:\left(\mathrm{2cos}\:\mathrm{60}^{\mathrm{o}} .\mathrm{cos}\:\mathrm{13}^{\mathrm{o}} \right)^{\mathrm{2}} −\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{cos}\:\mathrm{120}^{\mathrm{o}} +\mathrm{cos}\:\mathrm{26}^{\mathrm{o}} \right)+\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$=\:\mathrm{cos}\:^{\mathrm{2}} \mathrm{13}^{\mathrm{o}} +\frac{\mathrm{1}}{\mathrm{4}}−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{cos}\:\mathrm{26}^{\mathrm{o}} +\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$=\frac{\mathrm{3}}{\mathrm{4}}+\mathrm{cos}\:^{\mathrm{2}} \mathrm{13}^{\mathrm{o}} −\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{2cos}\:^{\mathrm{2}} \mathrm{13}^{\mathrm{o}} −\mathrm{1}\right) \\ $$$$=\:\frac{\mathrm{3}}{\mathrm{4}}+\frac{\mathrm{1}}{\mathrm{2}}\:=\:\frac{\mathrm{5}}{\mathrm{4}} \\ $$
Answered by Dwaipayan Shikari last updated on 03/Jul/20
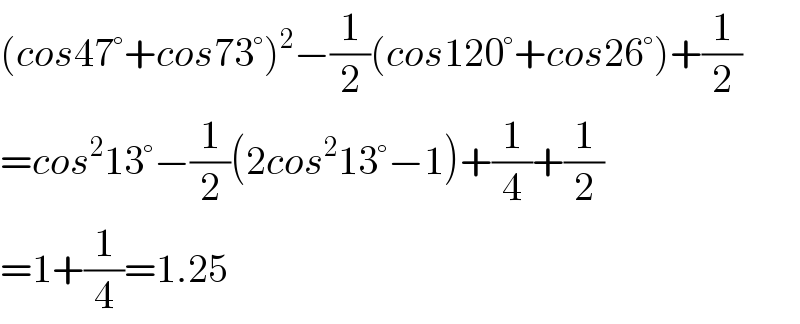
$$\left({cos}\mathrm{47}°+{cos}\mathrm{73}°\right)^{\mathrm{2}} −\frac{\mathrm{1}}{\mathrm{2}}\left({cos}\mathrm{120}°+{cos}\mathrm{26}°\right)+\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$={cos}^{\mathrm{2}} \mathrm{13}°−\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{2}{cos}^{\mathrm{2}} \mathrm{13}°−\mathrm{1}\right)+\frac{\mathrm{1}}{\mathrm{4}}+\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$=\mathrm{1}+\frac{\mathrm{1}}{\mathrm{4}}=\mathrm{1}.\mathrm{25} \\ $$
