Menu Close

calculate-cos-3x-x-2-x-1-2-dx-

Tinku Tara 0 Comments
Pin




Question Number 162016 by mathmax by abdo last updated on 25/Dec/21
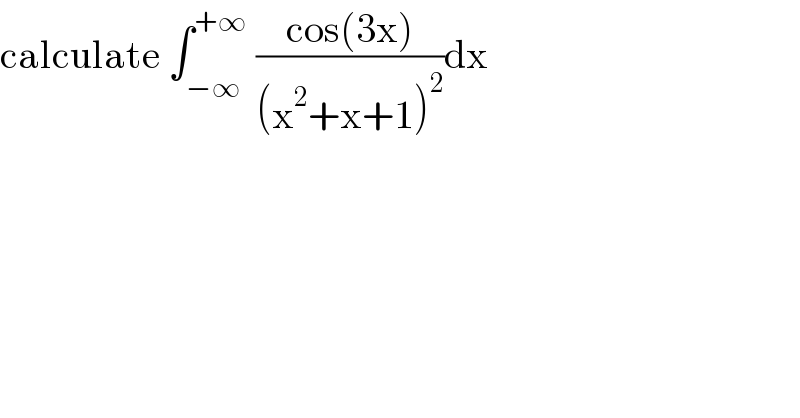
calculate ∫_(−∞) ^(+∞) ((cos(3x))/((x^2 +x+1)^2 ))dx
$$\mathrm{calculate}\:\int_{−\infty} ^{+\infty} \:\frac{\mathrm{cos}\left(\mathrm{3x}\right)}{\left(\mathrm{x}^{\mathrm{2}} +\mathrm{x}+\mathrm{1}\right)^{\mathrm{2}} }\mathrm{dx} \\ $$
Commented by MJS_new last updated on 25/Dec/21
I can solve the indefinite integral but it′s a long hard way...
$$\mathrm{I}\:\mathrm{can}\:\mathrm{solve}\:\mathrm{the}\:\mathrm{indefinite}\:\mathrm{integral}\:\mathrm{but}\:\mathrm{it}'\mathrm{s}\:\mathrm{a} \\ $$$$\mathrm{long}\:\mathrm{hard}\:\mathrm{way}… \\ $$
Commented by mathmax by abdo last updated on 25/Dec/21
use residus theorem sir
$$\mathrm{use}\:\mathrm{residus}\:\mathrm{theorem}\:\mathrm{sir} \\ $$
Answered by Ar Brandon last updated on 24/Mar/22
Υ=∫_(−∞) ^(+∞) ((cos3x)/((x^2 +x+1)^2 ))dx=Re∫_(−∞) ^(+∞) (e^(3ix) /((x^2 +x+1)^2 ))dx Let f(x)=(e^(3ix) /((x^2 +x+1)^2 )). Poles of f(x): e^((2/3)iπ) and e^(−(2/3)iπ) , order-2 Υ=Re∫_(−∞) ^(+∞) f(x)dx=Re(2iπRes(f, e^((2/3)iπ) )) Res (f, e^((2/3)iπ) )=lim_(x→e^((2/3)iπ) ) {(x−e^((2/3)iπ) )^2 f(x)}^((1)) =lim_(x→e^((2/3)iπ) ) {(e^(3ix) /((x−e^(−(2/3)iπ) )^2 ))}^((1)) =lim_(x→e^((2/3)iπ) ) {((3ie^(3ix) (x−e^(−(2/3)iπ) )^2 −2e^(3ix) (x−e^(−(2/3)iπ) ))/((x−e^(−(2/3)iπ) )^4 ))} =−(1/9)(9ie^(3i(−(1/2)+i((√3)/2))) +2(√3)ie^(3i(−(1/2)+i((√3)/2))) )=−(1/9)(9+2(√3))e^((−((3(√3))/2)−i((3−π)/2))) Υ=−((2π)/9)(9+2(√3))e^(−((3(√3))/2)) sin(((3−π)/2))=((2π)/9)(9+2(√3))e^(−((3(√3))/2)) cos((3/2))
$$\Upsilon=\int_{−\infty} ^{+\infty} \frac{\mathrm{cos3}{x}}{\left({x}^{\mathrm{2}} +{x}+\mathrm{1}\right)^{\mathrm{2}} }{dx}={Re}\int_{−\infty} ^{+\infty} \frac{{e}^{\mathrm{3}{ix}} }{\left({x}^{\mathrm{2}} +{x}+\mathrm{1}\right)^{\mathrm{2}} }{dx} \\ $$$$\mathrm{Let}\:{f}\left({x}\right)=\frac{{e}^{\mathrm{3}{ix}} }{\left({x}^{\mathrm{2}} +{x}+\mathrm{1}\right)^{\mathrm{2}} }.\:\mathrm{Poles}\:\mathrm{of}\:{f}\left({x}\right):\:{e}^{\frac{\mathrm{2}}{\mathrm{3}}{i}\pi} \:\mathrm{and}\:{e}^{−\frac{\mathrm{2}}{\mathrm{3}}{i}\pi} ,\:\mathrm{order}-\mathrm{2}\:\: \\ $$$$\Upsilon={Re}\int_{−\infty} ^{+\infty} {f}\left({x}\right){dx}={Re}\left(\mathrm{2}{i}\pi{Res}\left({f},\:{e}^{\frac{\mathrm{2}}{\mathrm{3}}{i}\pi} \right)\right) \\ $$$${Res}\:\left({f},\:{e}^{\frac{\mathrm{2}}{\mathrm{3}}{i}\pi} \right)=\underset{{x}\rightarrow{e}^{\frac{\mathrm{2}}{\mathrm{3}}{i}\pi} } {\mathrm{lim}}\left\{\left({x}−{e}^{\frac{\mathrm{2}}{\mathrm{3}}{i}\pi} \right)^{\mathrm{2}} {f}\left({x}\right)\right\}^{\left(\mathrm{1}\right)} =\underset{{x}\rightarrow{e}^{\frac{\mathrm{2}}{\mathrm{3}}{i}\pi} } {\mathrm{lim}}\left\{\frac{{e}^{\mathrm{3}{ix}} }{\left({x}−{e}^{−\frac{\mathrm{2}}{\mathrm{3}}{i}\pi} \right)^{\mathrm{2}} }\right\}^{\left(\mathrm{1}\right)} \\ $$$$=\underset{{x}\rightarrow{e}^{\frac{\mathrm{2}}{\mathrm{3}}{i}\pi} } {\mathrm{lim}}\left\{\frac{\mathrm{3}{ie}^{\mathrm{3}{ix}} \left({x}−{e}^{−\frac{\mathrm{2}}{\mathrm{3}}{i}\pi} \right)^{\mathrm{2}} −\mathrm{2}{e}^{\mathrm{3}{ix}} \left({x}−{e}^{−\frac{\mathrm{2}}{\mathrm{3}}{i}\pi} \right)}{\left({x}−{e}^{−\frac{\mathrm{2}}{\mathrm{3}}{i}\pi} \right)^{\mathrm{4}} }\right\} \\ $$$$=−\frac{\mathrm{1}}{\mathrm{9}}\left(\mathrm{9}{ie}^{\mathrm{3}{i}\left(−\frac{\mathrm{1}}{\mathrm{2}}+{i}\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\right)} +\mathrm{2}\sqrt{\mathrm{3}}{ie}^{\mathrm{3}{i}\left(−\frac{\mathrm{1}}{\mathrm{2}}+{i}\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\right)} \right)=−\frac{\mathrm{1}}{\mathrm{9}}\left(\mathrm{9}+\mathrm{2}\sqrt{\mathrm{3}}\right){e}^{\left(−\frac{\mathrm{3}\sqrt{\mathrm{3}}}{\mathrm{2}}−{i}\frac{\mathrm{3}−\pi}{\mathrm{2}}\right)} \\ $$$$\Upsilon=−\frac{\mathrm{2}\pi}{\mathrm{9}}\left(\mathrm{9}+\mathrm{2}\sqrt{\mathrm{3}}\right){e}^{−\frac{\mathrm{3}\sqrt{\mathrm{3}}}{\mathrm{2}}} \mathrm{sin}\left(\frac{\mathrm{3}−\pi}{\mathrm{2}}\right)=\frac{\mathrm{2}\pi}{\mathrm{9}}\left(\mathrm{9}+\mathrm{2}\sqrt{\mathrm{3}}\right){e}^{−\frac{\mathrm{3}\sqrt{\mathrm{3}}}{\mathrm{2}}} \mathrm{cos}\left(\frac{\mathrm{3}}{\mathrm{2}}\right) \\ $$
Commented by Mathspace last updated on 26/Dec/21
error of calculus..
$${error}\:{of}\:{calculus}.. \\ $$
Commented by Ar Brandon last updated on 26/Dec/21
Thank you for checking, Sir. Rectified!
$$\mathrm{Thank}\:\mathrm{you}\:\mathrm{for}\:\mathrm{checking},\:\mathrm{Sir}.\:\mathrm{Rectified}! \\ $$
Answered by Mathspace last updated on 26/Dec/21
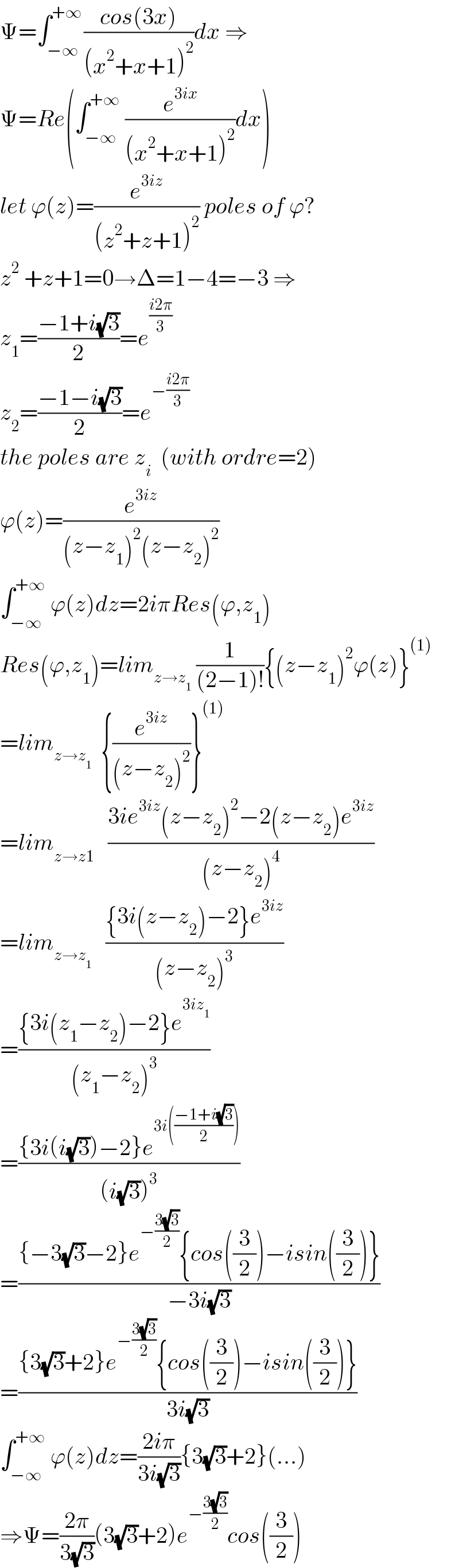
Ψ=∫_(−∞) ^(+∞ ) ((cos(3x))/((x^2 +x+1)^2 ))dx ⇒ Ψ=Re(∫_(−∞) ^(+∞) (e^(3ix) /((x^2 +x+1)^2 ))dx) let ϕ(z)=(e^(3iz) /((z^2 +z+1)^2 )) poles of ϕ? z^2 +z+1=0→Δ=1−4=−3 ⇒ z_1 =((−1+i(√3))/2)=e^((i2π)/3) z_2 =((−1−i(√3))/2)=e^(−((i2π)/3)) the poles are z_i (with ordre=2) ϕ(z)=(e^(3iz) /((z−z_1 )^2 (z−z_2 )^2 )) ∫_(−∞) ^(+∞) ϕ(z)dz=2iπRes(ϕ,z_1 ) Res(ϕ,z_1 )=lim_(z→z_1 ) (1/((2−1)!)){(z−z_1 )^2 ϕ(z)}^((1)) =lim_(z→z_1 ) {(e^(3iz) /((z−z_2 )^2 ))}^((1)) =lim_(z→z1) ((3ie^(3iz) (z−z_2 )^2 −2(z−z_2 )e^(3iz) )/((z−z_2 )^4 )) =lim_(z→z_1 ) (({3i(z−z_2 )−2}e^(3iz) )/((z−z_2 )^3 )) =(({3i(z_1 −z_2 )−2}e^(3iz_1 ) )/((z_1 −z_2 )^3 )) =(({3i(i(√3))−2}e^(3i(((−1+i(√3))/2))) )/((i(√3))^3 )) =(({−3(√3)−2}e^(−((3(√3))/2)) {cos((3/2))−isin((3/2))})/(−3i(√3))) =(({3(√3)+2}e^(−((3(√3))/2)) {cos((3/2))−isin((3/2))})/(3i(√3))) ∫_(−∞) ^(+∞) ϕ(z)dz=((2iπ)/(3i(√3))){3(√3)+2}(...) ⇒Ψ=((2π)/(3(√3)))(3(√3)+2)e^(−((3(√3))/2)) cos((3/2))
$$\Psi=\int_{−\infty} ^{+\infty\:} \frac{{cos}\left(\mathrm{3}{x}\right)}{\left({x}^{\mathrm{2}} +{x}+\mathrm{1}\right)^{\mathrm{2}} }{dx}\:\Rightarrow \\ $$$$\Psi={Re}\left(\int_{−\infty} ^{+\infty} \:\frac{{e}^{\mathrm{3}{ix}} }{\left({x}^{\mathrm{2}} +{x}+\mathrm{1}\right)^{\mathrm{2}} }{dx}\right) \\ $$$${let}\:\varphi\left({z}\right)=\frac{{e}^{\mathrm{3}{iz}} }{\left({z}^{\mathrm{2}} +{z}+\mathrm{1}\right)^{\mathrm{2}} }\:{poles}\:{of}\:\varphi? \\ $$$${z}^{\mathrm{2}} \:+{z}+\mathrm{1}=\mathrm{0}\rightarrow\Delta=\mathrm{1}−\mathrm{4}=−\mathrm{3}\:\Rightarrow \\ $$$${z}_{\mathrm{1}} =\frac{−\mathrm{1}+{i}\sqrt{\mathrm{3}}}{\mathrm{2}}={e}^{\frac{{i}\mathrm{2}\pi}{\mathrm{3}}} \\ $$$${z}_{\mathrm{2}} =\frac{−\mathrm{1}−{i}\sqrt{\mathrm{3}}}{\mathrm{2}}={e}^{−\frac{{i}\mathrm{2}\pi}{\mathrm{3}}} \\ $$$${the}\:{poles}\:{are}\:{z}_{{i}} \:\:\left({with}\:{ordre}=\mathrm{2}\right) \\ $$$$\varphi\left({z}\right)=\frac{{e}^{\mathrm{3}{iz}} }{\left({z}−{z}_{\mathrm{1}} \right)^{\mathrm{2}} \left({z}−{z}_{\mathrm{2}} \right)^{\mathrm{2}} } \\ $$$$\int_{−\infty} ^{+\infty} \:\varphi\left({z}\right){dz}=\mathrm{2}{i}\pi{Res}\left(\varphi,{z}_{\mathrm{1}} \right) \\ $$$${Res}\left(\varphi,{z}_{\mathrm{1}} \right)={lim}_{{z}\rightarrow{z}_{\mathrm{1}} } \:\frac{\mathrm{1}}{\left(\mathrm{2}−\mathrm{1}\right)!}\left\{\left({z}−{z}_{\mathrm{1}} \right)^{\mathrm{2}} \varphi\left({z}\right)\right\}^{\left(\mathrm{1}\right)} \\ $$$$={lim}_{{z}\rightarrow{z}_{\mathrm{1}} } \:\:\left\{\frac{{e}^{\mathrm{3}{iz}} }{\left({z}−{z}_{\mathrm{2}} \right)^{\mathrm{2}} }\right\}^{\left(\mathrm{1}\right)} \\ $$$$={lim}_{{z}\rightarrow{z}\mathrm{1}} \:\:\:\frac{\mathrm{3}{ie}^{\mathrm{3}{iz}} \left({z}−{z}_{\mathrm{2}} \right)^{\mathrm{2}} −\mathrm{2}\left({z}−{z}_{\mathrm{2}} \right){e}^{\mathrm{3}{iz}} }{\left({z}−{z}_{\mathrm{2}} \right)^{\mathrm{4}} } \\ $$$$={lim}_{{z}\rightarrow{z}_{\mathrm{1}} } \:\:\:\frac{\left\{\mathrm{3}{i}\left({z}−{z}_{\mathrm{2}} \right)−\mathrm{2}\right\}{e}^{\mathrm{3}{iz}} }{\left({z}−{z}_{\mathrm{2}} \right)^{\mathrm{3}} } \\ $$$$=\frac{\left\{\mathrm{3}{i}\left({z}_{\mathrm{1}} −{z}_{\mathrm{2}} \right)−\mathrm{2}\right\}{e}^{\mathrm{3}{iz}_{\mathrm{1}} } }{\left({z}_{\mathrm{1}} −{z}_{\mathrm{2}} \right)^{\mathrm{3}} } \\ $$$$=\frac{\left\{\mathrm{3}{i}\left({i}\sqrt{\mathrm{3}}\right)−\mathrm{2}\right\}{e}^{\mathrm{3}{i}\left(\frac{−\mathrm{1}+{i}\sqrt{\mathrm{3}}}{\mathrm{2}}\right)} }{\left({i}\sqrt{\mathrm{3}}\right)^{\mathrm{3}} } \\ $$$$=\frac{\left\{−\mathrm{3}\sqrt{\mathrm{3}}−\mathrm{2}\right\}{e}^{−\frac{\mathrm{3}\sqrt{\mathrm{3}}}{\mathrm{2}}} \left\{{cos}\left(\frac{\mathrm{3}}{\mathrm{2}}\right)−{isin}\left(\frac{\mathrm{3}}{\mathrm{2}}\right)\right\}}{−\mathrm{3}{i}\sqrt{\mathrm{3}}} \\ $$$$=\frac{\left\{\mathrm{3}\sqrt{\mathrm{3}}+\mathrm{2}\right\}{e}^{−\frac{\mathrm{3}\sqrt{\mathrm{3}}}{\mathrm{2}}} \left\{{cos}\left(\frac{\mathrm{3}}{\mathrm{2}}\right)−{isin}\left(\frac{\mathrm{3}}{\mathrm{2}}\right)\right\}}{\mathrm{3}{i}\sqrt{\mathrm{3}}} \\ $$$$\int_{−\infty} ^{+\infty} \:\varphi\left({z}\right){dz}=\frac{\mathrm{2}{i}\pi}{\mathrm{3}{i}\sqrt{\mathrm{3}}}\left\{\mathrm{3}\sqrt{\mathrm{3}}+\mathrm{2}\right\}\left(…\right) \\ $$$$\Rightarrow\Psi=\frac{\mathrm{2}\pi}{\mathrm{3}\sqrt{\mathrm{3}}}\left(\mathrm{3}\sqrt{\mathrm{3}}+\mathrm{2}\right){e}^{−\frac{\mathrm{3}\sqrt{\mathrm{3}}}{\mathrm{2}}} {cos}\left(\frac{\mathrm{3}}{\mathrm{2}}\right) \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *