Question Number 48360 by maxmathsup by imad last updated on 22/Nov/18
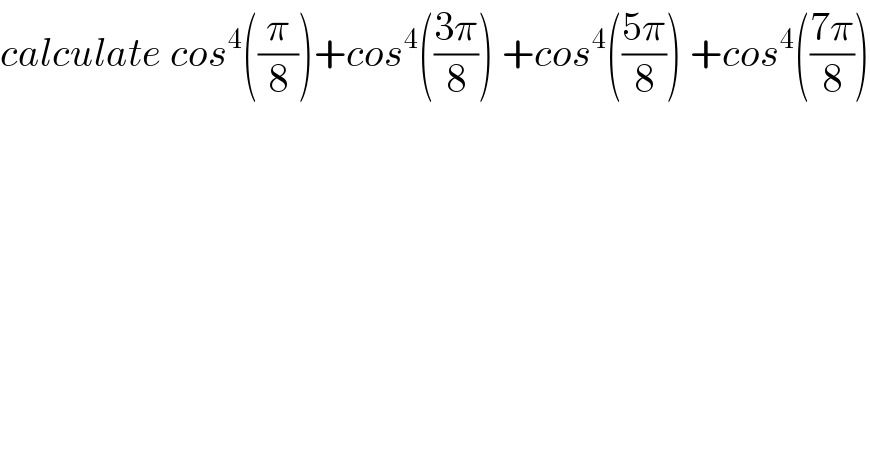
$${calculate}\:{cos}^{\mathrm{4}} \left(\frac{\pi}{\mathrm{8}}\right)+{cos}^{\mathrm{4}} \left(\frac{\mathrm{3}\pi}{\mathrm{8}}\right)\:+{cos}^{\mathrm{4}} \left(\frac{\mathrm{5}\pi}{\mathrm{8}}\right)\:+{cos}^{\mathrm{4}} \left(\frac{\mathrm{7}\pi}{\mathrm{8}}\right) \\ $$
Commented by Abdo msup. last updated on 23/Nov/18

$${S}={cos}^{\mathrm{4}} \left(\frac{\pi}{\mathrm{8}}\right)+{cos}^{\mathrm{4}} \left(\pi−\frac{\pi}{\mathrm{8}}\right)+{cos}^{\mathrm{4}} \left(\frac{\mathrm{3}\pi}{\mathrm{8}}\right)+{cos}^{\mathrm{4}} \left(\pi−\frac{\mathrm{3}\pi}{\mathrm{8}}\right) \\ $$$$=\mathrm{2}{cos}^{\mathrm{4}} \left(\frac{\pi}{\mathrm{8}}\right)+\mathrm{2}{cos}^{\mathrm{4}} \left(\frac{\mathrm{3}\pi}{\mathrm{8}}\right) \\ $$$$=\mathrm{2}{cos}^{\mathrm{4}} \left(\frac{\pi}{\mathrm{8}}\right)+\mathrm{2}{cos}^{\mathrm{4}} \left(\frac{\pi}{\mathrm{2}}\:−\frac{\pi}{\mathrm{8}}\right)=\mathrm{2}\left({cos}^{\mathrm{4}} \left(\frac{\pi}{\mathrm{8}}\right)+{sin}^{\mathrm{4}} \left(\frac{\pi}{\mathrm{8}}\right)\right) \\ $$$$=\mathrm{2}\left\{\:\left({cos}^{\mathrm{2}} \frac{\pi}{\mathrm{8}}\:+{sin}^{\mathrm{2}} \frac{\pi}{\mathrm{8}}\right)^{\mathrm{2}} −\mathrm{2}{cos}^{\mathrm{2}} \frac{\pi}{\mathrm{8}}{sin}^{\mathrm{2}} \frac{\pi}{\mathrm{8}}\right\} \\ $$$$=\mathrm{2}\left\{\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}}{sin}^{\mathrm{2}} \left(\frac{\pi}{\mathrm{4}}\right)\:=\mathrm{2}\left\{\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}}\frac{\mathrm{1}}{\mathrm{2}}\right\}=\mathrm{2}\frac{\mathrm{3}}{\mathrm{4}}\:=\frac{\mathrm{3}}{\mathrm{2}}\:.\right. \\ $$$$ \\ $$
Answered by behi83417@gmail.com last updated on 22/Nov/18

$${c}^{\mathrm{4}} \left(\frac{\pi}{\mathrm{8}}\right)={c}^{\mathrm{4}} \left(\frac{\mathrm{7}\pi}{\mathrm{8}}\right)=\left(\frac{\mathrm{1}+{c}\frac{\pi}{\mathrm{4}}}{\mathrm{2}}\right)^{\mathrm{2}} =\left(\frac{\mathrm{1}+\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}}{\mathrm{2}}\right)^{\mathrm{2}} =\frac{\mathrm{3}+\mathrm{2}\sqrt{\mathrm{2}}}{\mathrm{8}} \\ $$$${c}^{\mathrm{4}} \left(\frac{\mathrm{3}\pi}{\mathrm{8}}\right)={c}^{\mathrm{4}} \left(\frac{\mathrm{5}\pi}{\mathrm{8}}\right)=\left(\frac{\mathrm{1}+{c}\frac{\mathrm{3}\pi}{\mathrm{4}}}{\mathrm{2}}\right)^{\mathrm{2}} =\frac{\mathrm{3}−\mathrm{2}\sqrt{\mathrm{2}}}{\mathrm{8}} \\ $$$$\Rightarrow{S}=\mathrm{2}×\frac{\mathrm{3}+\mathrm{2}\sqrt{\mathrm{2}}}{\mathrm{8}}+\mathrm{2}×\frac{\mathrm{3}−\mathrm{2}\sqrt{\mathrm{2}}}{\mathrm{8}}=\frac{\mathrm{3}}{\mathrm{2}}. \\ $$
Answered by hknkrc46 last updated on 24/Dec/18
![α+β=π ⇒cos^(2k) α=cos^(2k) β (k∈N) α=(π/8) , β=((7π)/8) , k=2 ⇒cos^4 ((π/8))=cos^4 (((7π)/8)) ⇒cos^4 ((π/8))+cos^4 (((7π)/8))=2cos^4 ((π/8)) α=((3π)/8) , β=((5π)/8) , k=2 ⇒cos^4 (((3π)/8))=cos^4 (((5π)/8)) ⇒cos^4 (((3π)/8))+cos^4 (((5π)/8))=2cos^4 (((3π)/8)) 2cos^4 ((π/8))+2cos^4 (((3π)/8)) =2[cos^4 ((π/8))+cos^4 (((3π)/8))] =2[cos^4 ((π/8))+cos^4 ((π/2)−(π/8))] =2[cos^4 ((π/8))+sin^4 ((π/8))] =2[(cos^2 ((π/8))+sin^2 ((π/8)))^2 −((4cos^2 ((π/8))sin^2 ((π/8)))/2)] =2[1^2 −(((2cos ((π/8))sin ((π/8)))^2 )/2)] =2[1−((sin^2 ((π/4)))/2)]=2−sin^2 ((π/4)) =2−(((√2)/2))^2 =2−(1/2)=(3/2)](https://www.tinkutara.com/question/Q51117.png)
$$\:\alpha+\beta=\pi \\ $$$$\Rightarrow\mathrm{cos}\:^{\mathrm{2}{k}} \alpha=\mathrm{cos}\:^{\mathrm{2}{k}} \beta\:\left({k}\in\mathbb{N}\right) \\ $$$$\alpha=\frac{\pi}{\mathrm{8}}\:,\:\beta=\frac{\mathrm{7}\pi}{\mathrm{8}}\:,\:{k}=\mathrm{2} \\ $$$$\Rightarrow\mathrm{cos}\:^{\mathrm{4}} \left(\frac{\pi}{\mathrm{8}}\right)=\mathrm{cos}\:^{\mathrm{4}} \left(\frac{\mathrm{7}\pi}{\mathrm{8}}\right) \\ $$$$\Rightarrow\mathrm{cos}\:^{\mathrm{4}} \left(\frac{\pi}{\mathrm{8}}\right)+\mathrm{cos}\:^{\mathrm{4}} \left(\frac{\mathrm{7}\pi}{\mathrm{8}}\right)=\mathrm{2cos}\:^{\mathrm{4}} \left(\frac{\pi}{\mathrm{8}}\right) \\ $$$$\alpha=\frac{\mathrm{3}\pi}{\mathrm{8}}\:,\:\beta=\frac{\mathrm{5}\pi}{\mathrm{8}}\:,\:{k}=\mathrm{2} \\ $$$$\Rightarrow\mathrm{cos}\:^{\mathrm{4}} \left(\frac{\mathrm{3}\pi}{\mathrm{8}}\right)=\mathrm{cos}\:^{\mathrm{4}} \left(\frac{\mathrm{5}\pi}{\mathrm{8}}\right) \\ $$$$\Rightarrow\mathrm{cos}\:^{\mathrm{4}} \left(\frac{\mathrm{3}\pi}{\mathrm{8}}\right)+\mathrm{cos}\:^{\mathrm{4}} \left(\frac{\mathrm{5}\pi}{\mathrm{8}}\right)=\mathrm{2cos}\:^{\mathrm{4}} \left(\frac{\mathrm{3}\pi}{\mathrm{8}}\right) \\ $$$$\mathrm{2cos}\:^{\mathrm{4}} \left(\frac{\pi}{\mathrm{8}}\right)+\mathrm{2cos}\:^{\mathrm{4}} \left(\frac{\mathrm{3}\pi}{\mathrm{8}}\right) \\ $$$$=\mathrm{2}\left[\mathrm{cos}\:^{\mathrm{4}} \left(\frac{\pi}{\mathrm{8}}\right)+\mathrm{cos}\:^{\mathrm{4}} \left(\frac{\mathrm{3}\pi}{\mathrm{8}}\right)\right] \\ $$$$=\mathrm{2}\left[\mathrm{cos}\:^{\mathrm{4}} \left(\frac{\pi}{\mathrm{8}}\right)+\mathrm{cos}\:^{\mathrm{4}} \left(\frac{\pi}{\mathrm{2}}−\frac{\pi}{\mathrm{8}}\right)\right] \\ $$$$=\mathrm{2}\left[\mathrm{cos}\:^{\mathrm{4}} \left(\frac{\pi}{\mathrm{8}}\right)+\mathrm{sin}\:^{\mathrm{4}} \left(\frac{\pi}{\mathrm{8}}\right)\right] \\ $$$$=\mathrm{2}\left[\left(\mathrm{cos}\:^{\mathrm{2}} \left(\frac{\pi}{\mathrm{8}}\right)+\mathrm{sin}\:^{\mathrm{2}} \left(\frac{\pi}{\mathrm{8}}\right)\right)^{\mathrm{2}} −\frac{\mathrm{4cos}\:^{\mathrm{2}} \left(\frac{\pi}{\mathrm{8}}\right)\mathrm{sin}\:^{\mathrm{2}} \left(\frac{\pi}{\mathrm{8}}\right)}{\mathrm{2}}\right] \\ $$$$=\mathrm{2}\left[\mathrm{1}^{\mathrm{2}} −\frac{\left(\mathrm{2cos}\:\left(\frac{\pi}{\mathrm{8}}\right)\mathrm{sin}\:\left(\frac{\pi}{\mathrm{8}}\right)\right)^{\mathrm{2}} }{\mathrm{2}}\right] \\ $$$$=\mathrm{2}\left[\mathrm{1}−\frac{\mathrm{sin}^{\mathrm{2}} \:\left(\frac{\pi}{\mathrm{4}}\right)}{\mathrm{2}}\right]=\mathrm{2}−\mathrm{sin}\:^{\mathrm{2}} \left(\frac{\pi}{\mathrm{4}}\right) \\ $$$$=\mathrm{2}−\left(\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\right)^{\mathrm{2}} =\mathrm{2}−\frac{\mathrm{1}}{\mathrm{2}}=\frac{\mathrm{3}}{\mathrm{2}} \\ $$
