Menu Close

calculate-cos-arctan-2x-1-x-2-2x-2-dx-

Tinku Tara 0 Comments
Pin




Question Number 101268 by mathmax by abdo last updated on 01/Jul/20
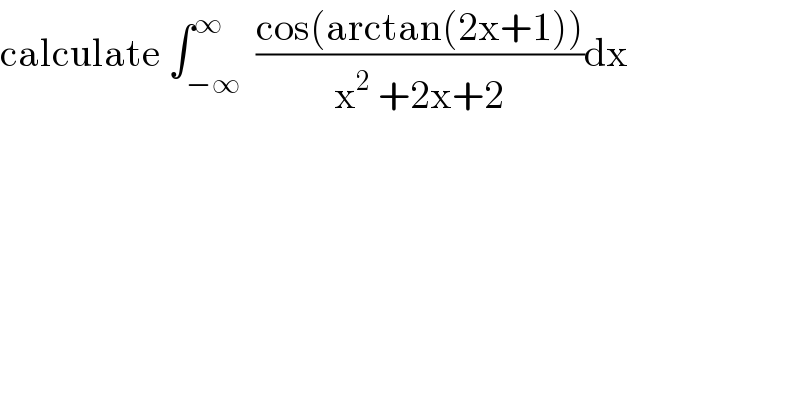
calculate ∫_(−∞) ^∞ ((cos(arctan(2x+1)))/(x^2 +2x+2))dx
$$\mathrm{calculate}\:\int_{−\infty} ^{\infty} \:\frac{\mathrm{cos}\left(\mathrm{arctan}\left(\mathrm{2x}+\mathrm{1}\right)\right)}{\mathrm{x}^{\mathrm{2}} \:+\mathrm{2x}+\mathrm{2}}\mathrm{dx} \\ $$
Answered by mathmax by abdo last updated on 02/Jul/20
I =∫_(−∞) ^(+∞) ((cos(arctan(2x+1)))/(x^2 +2x+2))dx changement 2x+1 =t give I =∫_(−∞) ^(+∞) ((cos(arctant))/((((t−1)/2))^2 +2(((t−1)/2))+2)) (dt/2) =(1/2) ∫_(−∞) ^(+∞) ((cos(arctant))/((((t−1)^2 )/4)+t+1)) dt =2 ∫_(−∞) ^(+∞) ((cos(arctant))/((t−1)^2 +4t+4))dt =2 ∫_(−∞) ^(+∞) ((cos(arctant))/(t^2 −2t+1 +4t +4))dt =2 ∫_(−∞) ^(+∞) ((cos(arctant))/(t^2 +2t+5))dt =2 Re(∫_(−∞) ^(+∞) (e^(iarctant) /(t^(2 ) +2t +5))dt) let ϕ(z) =(e^(iarctanz) /(z^2 +2z +5)) poles of ϕ? z^2 +2z +5 =0→Δ^′ =1−5 =−4 ⇒z_1 =−1+2i and z_2 =−1−2i residus theorem give ∫_(−∞) ^(+∞) ϕ(z)dz =2iπ Res(ϕ,z_1 ) ϕ(z) =(e^(iarctan(z)) /((z−z_1 )(z−z_2 ))) ⇒Res(ϕ,z_1 ) =(e^(iarctanz_1 ) /(z_1 −z_2 )) =(e^(iarctan(−1+2i)) /(4i)) ⇒ ∫_(−∞) ^(+∞) ϕ(z)dz =2iπ ×(e^(iarctan(−1+2i)) /(4i)) =(π/2) e^(iarctan(−1+2i)) we know arctanz =(1/(2i))ln(((1+iz)/(1−iz))) ⇒arctan(−1+2i) =(1/(2i))ln(((1+i(−1+2i))/(1−i(−1+2i)))) =(1/(2i))ln(((1−i−2)/(1+i+2))) =(1/(2i))ln(((−1−i)/(3+i))) also ((−1−i)/(3+i)) =(((√2)e^(i((5π)/4)) )/( (√(10))e^(iarctan((1/3))) )) =((√2)/( (√(10)))) e^(i(((5π)/4)−arctan((1/3)))) ⇒ arctan(−1+2i) =(1/(2i))ln(((√2)/( (√(10))))) +(1/(2i))×i(((5π)/4)−arctan((1/3))) =(1/(4i))ln((1/5))+(1/2)(((5π)/4) −arctan((1/3))) ⇒ ∫_(−∞) ^(+∞) ϕ(z)dz =(π/2)e^(i((1/(4i))ln((1/5))+((5π)/8)−(1/2)arctan((1/3)))) =(π/2)e^(−((ln5)/4)) { cos(((5π)/8)−(1/2)arctan((1/3))) +isin(....)} ⇒ I =π e^(−((ln5)/4)) cos(((5π)/8)−(1/2)arctan((1/3)))
$$\mathrm{I}\:=\int_{−\infty} ^{+\infty} \:\frac{\mathrm{cos}\left(\mathrm{arctan}\left(\mathrm{2x}+\mathrm{1}\right)\right)}{\mathrm{x}^{\mathrm{2}} \:+\mathrm{2x}+\mathrm{2}}\mathrm{dx}\:\mathrm{changement}\:\mathrm{2x}+\mathrm{1}\:=\mathrm{t}\:\mathrm{give} \\ $$$$\mathrm{I}\:=\int_{−\infty} ^{+\infty} \:\frac{\mathrm{cos}\left(\mathrm{arctant}\right)}{\left(\frac{\mathrm{t}−\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} \:+\mathrm{2}\left(\frac{\mathrm{t}−\mathrm{1}}{\mathrm{2}}\right)+\mathrm{2}}\:\frac{\mathrm{dt}}{\mathrm{2}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\:\int_{−\infty} ^{+\infty} \:\frac{\mathrm{cos}\left(\mathrm{arctant}\right)}{\frac{\left(\mathrm{t}−\mathrm{1}\right)^{\mathrm{2}} }{\mathrm{4}}+\mathrm{t}+\mathrm{1}}\:\mathrm{dt}\:=\mathrm{2}\:\int_{−\infty} ^{+\infty} \:\frac{\mathrm{cos}\left(\mathrm{arctant}\right)}{\left(\mathrm{t}−\mathrm{1}\right)^{\mathrm{2}} +\mathrm{4t}+\mathrm{4}}\mathrm{dt} \\ $$$$=\mathrm{2}\:\int_{−\infty} ^{+\infty} \:\frac{\mathrm{cos}\left(\mathrm{arctant}\right)}{\mathrm{t}^{\mathrm{2}} −\mathrm{2t}+\mathrm{1}\:+\mathrm{4t}\:+\mathrm{4}}\mathrm{dt}\:=\mathrm{2}\:\int_{−\infty} ^{+\infty} \:\frac{\mathrm{cos}\left(\mathrm{arctant}\right)}{\mathrm{t}^{\mathrm{2}} +\mathrm{2t}+\mathrm{5}}\mathrm{dt} \\ $$$$=\mathrm{2}\:\mathrm{Re}\left(\int_{−\infty} ^{+\infty} \:\frac{\mathrm{e}^{\mathrm{iarctant}} }{\mathrm{t}^{\mathrm{2}\:} \:+\mathrm{2t}\:+\mathrm{5}}\mathrm{dt}\right)\:\mathrm{let}\:\varphi\left(\mathrm{z}\right)\:=\frac{\mathrm{e}^{\mathrm{iarctanz}} }{\mathrm{z}^{\mathrm{2}} \:+\mathrm{2z}\:+\mathrm{5}}\:\:\mathrm{poles}\:\mathrm{of}\:\varphi? \\ $$$$\mathrm{z}^{\mathrm{2}} \:+\mathrm{2z}\:+\mathrm{5}\:=\mathrm{0}\rightarrow\Delta^{'} \:=\mathrm{1}−\mathrm{5}\:=−\mathrm{4}\:\Rightarrow\mathrm{z}_{\mathrm{1}} =−\mathrm{1}+\mathrm{2i}\:\mathrm{and}\:\mathrm{z}_{\mathrm{2}} =−\mathrm{1}−\mathrm{2i} \\ $$$$\mathrm{residus}\:\mathrm{theorem}\:\mathrm{give}\:\int_{−\infty} ^{+\infty} \:\varphi\left(\mathrm{z}\right)\mathrm{dz}\:=\mathrm{2i}\pi\:\mathrm{Res}\left(\varphi,\mathrm{z}_{\mathrm{1}} \right) \\ $$$$\varphi\left(\mathrm{z}\right)\:=\frac{\mathrm{e}^{\mathrm{iarctan}\left(\mathrm{z}\right)} }{\left(\mathrm{z}−\mathrm{z}_{\mathrm{1}} \right)\left(\mathrm{z}−\mathrm{z}_{\mathrm{2}} \right)}\:\Rightarrow\mathrm{Res}\left(\varphi,\mathrm{z}_{\mathrm{1}} \right)\:=\frac{\mathrm{e}^{\mathrm{iarctanz}_{\mathrm{1}} } }{\mathrm{z}_{\mathrm{1}} −\mathrm{z}_{\mathrm{2}} }\:=\frac{\mathrm{e}^{\mathrm{iarctan}\left(−\mathrm{1}+\mathrm{2i}\right)} }{\mathrm{4i}}\:\Rightarrow \\ $$$$\int_{−\infty} ^{+\infty} \:\varphi\left(\mathrm{z}\right)\mathrm{dz}\:=\mathrm{2i}\pi\:×\frac{\mathrm{e}^{\mathrm{iarctan}\left(−\mathrm{1}+\mathrm{2i}\right)} }{\mathrm{4i}}\:=\frac{\pi}{\mathrm{2}}\:\mathrm{e}^{\mathrm{iarctan}\left(−\mathrm{1}+\mathrm{2i}\right)} \\ $$$$\mathrm{we}\:\mathrm{know}\:\mathrm{arctanz}\:=\frac{\mathrm{1}}{\mathrm{2i}}\mathrm{ln}\left(\frac{\mathrm{1}+\mathrm{iz}}{\mathrm{1}−\mathrm{iz}}\right)\:\Rightarrow\mathrm{arctan}\left(−\mathrm{1}+\mathrm{2i}\right)\:=\frac{\mathrm{1}}{\mathrm{2i}}\mathrm{ln}\left(\frac{\mathrm{1}+\mathrm{i}\left(−\mathrm{1}+\mathrm{2i}\right)}{\mathrm{1}−\mathrm{i}\left(−\mathrm{1}+\mathrm{2i}\right)}\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{2i}}\mathrm{ln}\left(\frac{\mathrm{1}−\mathrm{i}−\mathrm{2}}{\mathrm{1}+\mathrm{i}+\mathrm{2}}\right)\:=\frac{\mathrm{1}}{\mathrm{2i}}\mathrm{ln}\left(\frac{−\mathrm{1}−\mathrm{i}}{\mathrm{3}+\mathrm{i}}\right)\:\mathrm{also} \\ $$$$\frac{−\mathrm{1}−\mathrm{i}}{\mathrm{3}+\mathrm{i}}\:=\frac{\sqrt{\mathrm{2}}\mathrm{e}^{\mathrm{i}\frac{\mathrm{5}\pi}{\mathrm{4}}} }{\:\sqrt{\mathrm{10}}\mathrm{e}^{\mathrm{iarctan}\left(\frac{\mathrm{1}}{\mathrm{3}}\right)} }\:=\frac{\sqrt{\mathrm{2}}}{\:\sqrt{\mathrm{10}}}\:\mathrm{e}^{\mathrm{i}\left(\frac{\mathrm{5}\pi}{\mathrm{4}}−\mathrm{arctan}\left(\frac{\mathrm{1}}{\mathrm{3}}\right)\right)} \:\Rightarrow \\ $$$$\mathrm{arctan}\left(−\mathrm{1}+\mathrm{2i}\right)\:=\frac{\mathrm{1}}{\mathrm{2i}}\mathrm{ln}\left(\frac{\sqrt{\mathrm{2}}}{\:\sqrt{\mathrm{10}}}\right)\:+\frac{\mathrm{1}}{\mathrm{2i}}×\mathrm{i}\left(\frac{\mathrm{5}\pi}{\mathrm{4}}−\mathrm{arctan}\left(\frac{\mathrm{1}}{\mathrm{3}}\right)\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{4i}}\mathrm{ln}\left(\frac{\mathrm{1}}{\mathrm{5}}\right)+\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{\mathrm{5}\pi}{\mathrm{4}}\:−\mathrm{arctan}\left(\frac{\mathrm{1}}{\mathrm{3}}\right)\right)\:\Rightarrow \\ $$$$\int_{−\infty} ^{+\infty} \:\varphi\left(\mathrm{z}\right)\mathrm{dz}\:=\frac{\pi}{\mathrm{2}}\mathrm{e}^{\mathrm{i}\left(\frac{\mathrm{1}}{\mathrm{4i}}\mathrm{ln}\left(\frac{\mathrm{1}}{\mathrm{5}}\right)+\frac{\mathrm{5}\pi}{\mathrm{8}}−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{arctan}\left(\frac{\mathrm{1}}{\mathrm{3}}\right)\right)} \\ $$$$=\frac{\pi}{\mathrm{2}}\mathrm{e}^{−\frac{\mathrm{ln5}}{\mathrm{4}}} \:\left\{\:\mathrm{cos}\left(\frac{\mathrm{5}\pi}{\mathrm{8}}−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{arctan}\left(\frac{\mathrm{1}}{\mathrm{3}}\right)\right)\:+\mathrm{isin}\left(….\right)\right\}\:\Rightarrow \\ $$$$\mathrm{I}\:=\pi\:\mathrm{e}^{−\frac{\mathrm{ln5}}{\mathrm{4}}} \:\mathrm{cos}\left(\frac{\mathrm{5}\pi}{\mathrm{8}}−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{arctan}\left(\frac{\mathrm{1}}{\mathrm{3}}\right)\right) \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *