Question Number 98587 by mathmax by abdo last updated on 14/Jun/20
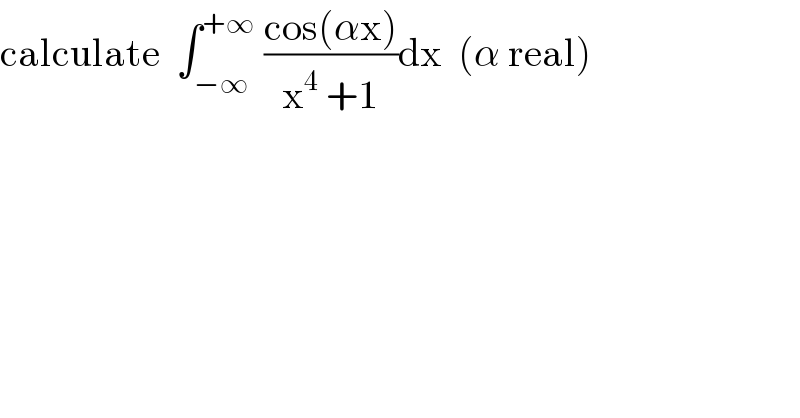
$$\mathrm{calculate}\:\:\int_{−\infty} ^{+\infty} \:\frac{\mathrm{cos}\left(\alpha\mathrm{x}\right)}{\mathrm{x}^{\mathrm{4}} \:+\mathrm{1}}\mathrm{dx}\:\:\left(\alpha\:\mathrm{real}\right) \\ $$
Answered by mathmax by abdo last updated on 15/Jun/20

$$\mathrm{A}\:=\int_{−\infty} ^{+\infty} \:\frac{\mathrm{cos}\left(\alpha\mathrm{x}\right)}{\mathrm{x}^{\mathrm{4}} \:+\mathrm{1}}\mathrm{dx}\:\Rightarrow\:\mathrm{A}\:=\mathrm{Re}\left(\int_{−\infty} ^{+\infty} \:\frac{\mathrm{e}^{\mathrm{i}\alpha\mathrm{x}} }{\mathrm{x}^{\mathrm{4}} \:+\mathrm{1}}\mathrm{dx}\right)\:\mathrm{let}\:\varphi\left(\mathrm{z}\right)\:=\frac{\mathrm{e}^{\mathrm{i}\alpha\mathrm{z}} }{\mathrm{z}^{\mathrm{4}} \:+\mathrm{1}} \\ $$$$\mathrm{we}\:\mathrm{hsve}\:\varphi\left(\mathrm{z}\right)\:=\frac{\mathrm{e}^{\mathrm{i}\alpha\mathrm{z}} }{\left(\mathrm{z}^{\mathrm{2}} −\mathrm{i}\right)\left(\mathrm{z}^{\mathrm{2}} \:+\mathrm{i}\right)}\:=\frac{\mathrm{e}^{\mathrm{i}\alpha\mathrm{z}} }{\left(\mathrm{z}^{\mathrm{2}} \:−\mathrm{e}^{\frac{\mathrm{i}\pi}{\mathrm{2}}} \right)\left(\mathrm{z}^{\mathrm{2}} \:−\mathrm{e}^{−\frac{\mathrm{i}\pi}{\mathrm{2}}} \right)} \\ $$$$=\frac{\mathrm{e}^{\mathrm{i}\alpha\mathrm{z}} }{\left(\mathrm{z}−\mathrm{e}^{\frac{\mathrm{i}\pi}{\mathrm{4}}} \right)\left(\mathrm{z}+\mathrm{e}^{\frac{\mathrm{i}\pi}{\mathrm{4}}} \right)\left(\mathrm{z}−\mathrm{e}^{−\frac{\mathrm{i}\pi}{\mathrm{4}}} \right)\left(\mathrm{z}+\mathrm{e}^{−\frac{\mathrm{i}\pi}{\mathrm{4}}} \right)}\:\:\mathrm{residus}\:\mathrm{theorem}\:\mathrm{give} \\ $$$$\int_{−\infty} ^{+\infty} \:\varphi\left(\mathrm{z}\right)\mathrm{dz}\:=\mathrm{2i}\pi\:\left\{\:\mathrm{Res}\left(\varphi,\mathrm{e}^{\frac{\mathrm{i}\pi}{\mathrm{4}}} \right)+\mathrm{Res}\left(\varphi,−\mathrm{e}^{−\frac{\mathrm{i}\pi}{\mathrm{4}}} \right)\right\}\:\:\mathrm{we}\:\mathrm{have} \\ $$$$\mathrm{Res}\left(\varphi,\mathrm{e}^{\mathrm{i}\frac{\pi}{\mathrm{4}}} \right)\:=\mathrm{lim}_{\mathrm{z}\rightarrow\mathrm{e}^{\frac{\mathrm{i}\pi}{\mathrm{4}}} } \:\:\left(\mathrm{z}−\mathrm{e}^{\frac{\mathrm{i}\pi}{\mathrm{4}}} \right)\varphi\left(\mathrm{z}\right)\:=\mathrm{lim}_{\mathrm{z}\rightarrow\mathrm{e}^{\frac{\mathrm{i}\pi}{\mathrm{4}}} } \:\:\:\:\frac{\mathrm{e}^{\mathrm{i}\alpha\mathrm{e}^{\frac{\mathrm{i}\pi}{\mathrm{4}}} } }{\mathrm{2e}^{\frac{\mathrm{i}\pi}{\mathrm{4}}} \left(\mathrm{2isin}\left(\frac{\pi}{\mathrm{2}}\right)\right)} \\ $$$$=\frac{\mathrm{e}^{−\frac{\mathrm{i}\pi}{\mathrm{4}}} \:×\mathrm{e}^{\mathrm{i}\alpha\left(\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}+\frac{\mathrm{i}}{\:\sqrt{\mathrm{2}}}\right)} }{\mathrm{4i}}\:=\frac{\mathrm{e}^{−\frac{\mathrm{i}\pi}{\mathrm{4}}} \:×\mathrm{e}^{−\frac{\alpha}{\:\sqrt{\mathrm{2}}}} \:\mathrm{e}^{\frac{\mathrm{i}\alpha}{\:\sqrt{\mathrm{2}}}} }{\mathrm{4i}}\:=\frac{\mathrm{e}^{−\frac{\alpha}{\:\sqrt{\mathrm{2}}}} }{\mathrm{4i}}\:\mathrm{e}^{\mathrm{i}\left(−\frac{\pi}{\mathrm{4}}+\frac{\alpha}{\:\sqrt{\mathrm{2}}}\right)} \\ $$$$\mathrm{Res}\left(\varphi,−\mathrm{e}^{−\frac{\mathrm{i}\pi}{\mathrm{4}}} \right)\:=\mathrm{lim}_{\mathrm{z}\rightarrow−\mathrm{e}^{−\frac{\mathrm{i}\pi}{\mathrm{4}}} } \:\:\left(\mathrm{z}+\mathrm{e}^{\frac{\mathrm{i}\pi}{\mathrm{4}}} \right)\varphi\left(\mathrm{z}\right) \\ $$$$=\mathrm{lim}_{\mathrm{z}\rightarrow−\mathrm{e}^{−\frac{\mathrm{i}\pi}{\mathrm{4}}} } \:\:\:\:\:\frac{\mathrm{e}^{\mathrm{i}\alpha\:\left(−\mathrm{e}^{−\frac{\mathrm{i}\pi}{\mathrm{4}}} \right)} }{−\mathrm{2}\:\mathrm{e}^{−\frac{\mathrm{i}\pi}{\mathrm{4}}} \left(−\mathrm{2i}\right)}\:=\frac{\mathrm{e}^{\frac{\mathrm{i}\pi}{\mathrm{4}}} }{\mathrm{4i}}\:\mathrm{e}^{\mathrm{i}\alpha\left(−\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}+\frac{\mathrm{i}}{\:\sqrt{\mathrm{2}}}\right)} \:=\frac{\mathrm{e}^{−\frac{\alpha}{\:\sqrt{\mathrm{2}}}} }{\mathrm{4i}}\:\mathrm{e}^{\mathrm{i}\left(\frac{\pi}{\mathrm{4}}−\frac{\alpha}{\:\sqrt{\mathrm{2}}}\right)} \:\Rightarrow \\ $$$$\int_{−\infty} ^{+\infty} \:\varphi\left(\mathrm{z}\right)\mathrm{dz}\:=\mathrm{2i}\pi\left\{\:\frac{\mathrm{e}^{−\frac{\alpha}{\:\sqrt{\mathrm{2}}}} }{\mathrm{4i}}\:\mathrm{e}^{\mathrm{i}\left(−\frac{\pi}{\mathrm{4}}\:+\frac{\alpha}{\:\sqrt{\mathrm{2}}}\right)} \:+\frac{\mathrm{e}^{−\frac{\alpha}{\:\sqrt{\mathrm{2}}}} }{\mathrm{4i}}\:\mathrm{e}^{\mathrm{i}\left(\frac{\pi}{\mathrm{4}}−\frac{\alpha}{\:\sqrt{\mathrm{2}}}\right)} \right\} \\ $$$$=\frac{\pi}{\mathrm{2}}\:\mathrm{e}^{−\frac{\alpha}{\:\sqrt{\mathrm{2}}}} \left\{\:\mathrm{e}^{\mathrm{i}\left(\frac{\pi}{\mathrm{4}}−\frac{\alpha}{\:\sqrt{\mathrm{2}}}\right)} \:+\mathrm{e}^{−\mathrm{i}\left(\frac{\pi}{\mathrm{4}}−\frac{\alpha}{\:\sqrt{\mathrm{2}}}\right)} \right\}\:\:=\frac{\pi}{\mathrm{2}}\:\mathrm{e}^{−\frac{\alpha}{\:\sqrt{\mathrm{2}}}} \:\:\:\:\left(\mathrm{2cos}\left(\frac{\pi}{\mathrm{4}}−\frac{\alpha}{\:\sqrt{\mathrm{2}}}\right)\right) \\ $$$$=\pi\:\mathrm{e}^{−\frac{\alpha}{\:\sqrt{\mathrm{2}}}} \:\mathrm{cos}\left(\frac{\pi}{\mathrm{4}}\:−\frac{\alpha}{\:\sqrt{\mathrm{2}}}\right)\:\Rightarrow\:\mathrm{A}\:=\pi\:\mathrm{e}^{−\frac{\alpha}{\:\sqrt{\mathrm{2}}}} \:\mathrm{cos}\left(\frac{\pi}{\mathrm{4}}−\frac{\alpha}{\:\sqrt{\mathrm{2}}}\right)\:. \\ $$$$ \\ $$
