calculate-D-x-2-x-y-dxdy-with-D-is-the-triangle-0-A-B-0-origin-A-1-0-B-0-1-

Question Number 89314 by abdomathmax last updated on 16/Apr/20

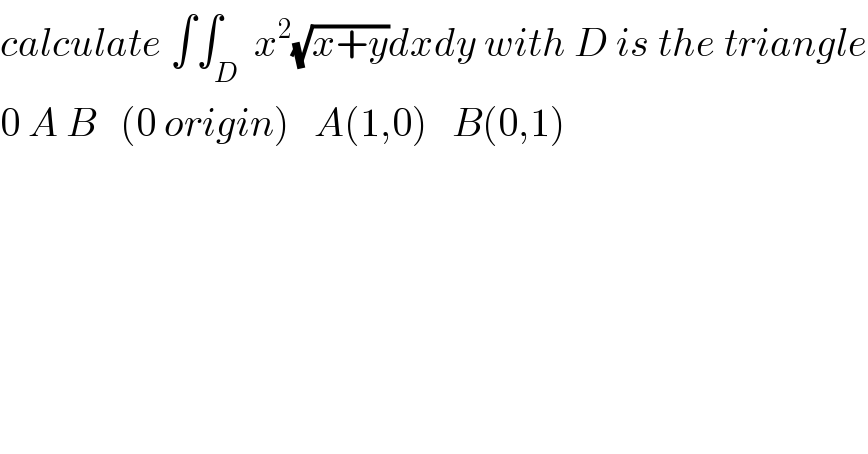
c a l c u l a t e \int \int_{D} x^{2} \sqrt{x + y} d x d y w i t h D i s t h e t r i a n g l e

0 A B (0 o r i g i n) A (1, 0) B (0, 1)

Commented by abdomathmax last updated on 18/Apr/20

t h e e q u a t i o n o f l i n e (A B) i s x + y = 1 \Rightarrow y = 1 - x \Rightarrow

\int \int_{D} x^{2} \sqrt{x + y} d x d y = \int_{0}^{1} (\int_{0}^{1 - x} \sqrt{x + y} d y) x^{2} d x w e h a v e

\int_{0}^{1 - x} \sqrt{x + y} d y =_{x + y = t^{2}} \int_{\sqrt{x}}^{1} t (2 t) d t

= 2 \int_{\sqrt{x}}^{1} t^{2} d t = \frac{2}{3} {[t^{3}]}_{\sqrt{x}}^{1} = \frac{2}{3} (1 - x \sqrt{x}) \Rightarrow

I = \frac{2}{3} \int_{0}^{1} (1 - x \sqrt{x}) x^{2} d x

= \frac{2}{3} \int_{0}^{1} x^{2} d x - \frac{2}{3} \int_{0}^{1} x^{3} \sqrt{x} d x

= \frac{2}{9} - \frac{2}{3} \int_{0}^{1} x^{3} \sqrt{x} d x w e h a v e

\int_{0}^{1} x^{3} \sqrt{x} d x =_{\sqrt{x} = u} \int_{0}^{1} u^{6} . u (2 u) d u

= 2 \int_{0}^{1} u^{8} d u = \frac{2}{9} \Rightarrow

I = \frac{2}{9} - \frac{2}{3} \times \frac{2}{9} = \frac{2}{9} (1 - \frac{2}{3}) = \frac{2}{9} \times \frac{1}{3} = \frac{2}{27}