calculate-D-x-2-y-2-z-2-dxdydz-with-D-x-y-z-0-x-1-1-y-2-2-z-3-

Question Number 61645 by maxmathsup by imad last updated on 05/Jun/19

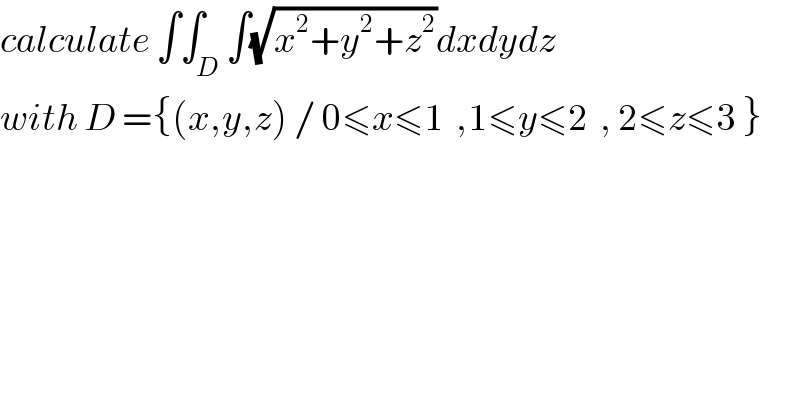
c a l c u l a t e \int \int_{D} \int \sqrt{x^{2} + y^{2} + z^{2}} d x d y d z

w i t h D = {(x, y, z) / 0 ⩽ x ⩽ 1, 1 ⩽ y ⩽ 2, 2 ⩽ z ⩽ 3}

Commented by maxmathsup by imad last updated on 06/Jun/19

l e t I = \int \int \int_{D} \sqrt{x^{2} + y^{2} + z^{2}} d x d y d z \Rightarrow I = \int_{2}^{3} A (z) d z w i t h

A (z) = \int \int_{w} \sqrt{x^{2} + y^{2} + z^{2}} d x d y l e t c o n s i d e r t h e d i f f e o m o r p h i s m

x = r c o s θ a n d y = r s i n θ w e h a v e 0 ⩽ x ⩽ 1 a n d 1 ⩽ y ⩽ 2 \Rightarrow

1 ⩽ x^{2} + y^{2} ⩽ 5 \Rightarrow 1 ⩽ r^{2} ⩽ 5 \Rightarrow 1 ⩽ r ⩽ \sqrt{5} \Rightarrow

A (z) = \int \int_{1 ⩽ r ⩽ \sqrt{5} a n d 0 ⩽ θ ⩽ \frac{π}{2}} \sqrt{r^{2} + z^{2}} r d r d θ

= \frac{π}{2} \int_{1}^{\sqrt{5}} r {(r^{2} + z^{2})}^{\frac{1}{2}} d r = \frac{π}{2} {[\frac{1}{3} {(r^{2} + z^{2})}^{\frac{3}{2}}]}_{1}^{\sqrt{5}} = \frac{π}{6} {{(z^{2} + 5)}^{\frac{3}{2}} - {(z^{2} + 1)}^{\frac{3}{2}}} \Rightarrow

I = \frac{π}{6} \int_{2}^{3} {(z^{2} + 5)}^{\frac{3}{2}} d z - \frac{π}{6} \int_{2}^{3} {(z^{2} + 1)}^{\frac{3}{2}} d z

\int_{2}^{3} {(1 + z^{2})}^{\frac{3}{2}} d z =_{z = s h (t)} \int_{a r g s h (2)}^{a r g s h (3)} {({c h}^{2} t)}^{\frac{3}{2}} c h (t) d t = \int_{l n (2 + \sqrt{5})}^{l n (3 + \sqrt{10})} {c h}^{4} t d t

= \int_{l n (2 + \sqrt{5})}^{l n (3 + 10)} {(\frac{1 + c h (2 t)}{2})}^{2} d t = \frac{1}{4} \int_{l n (2 + \sqrt{5})}^{l n (3 + \sqrt{10})} (1 + 2 c h (2 t) + {c h}^{2} (2 t)) d t

= \frac{1}{4} {l n (3 + \sqrt{10}) - l n (2 + \sqrt{5})) + \frac{1}{4} {[s h (2 t)]}_{l n (2 + \sqrt{5})}^{l n (3 + \sqrt{10})} + \frac{1}{8} \int_{l n (2 + \sqrt{5})}^{l n (3 + \sqrt{10})} (1 + c h (4 t)) d t

= \dots . . r e s t t o a c h e i v e t h e c a l c u l u s f o r t h e i n t e g r a l \int_{2}^{3} {(z^{2} + 5)}^{\frac{3}{2}} d z

w e d o t h e c h a n g . z = \sqrt{5} s h (t) \dots .