Question Number 57321 by turbo msup by abdo last updated on 02/Apr/19
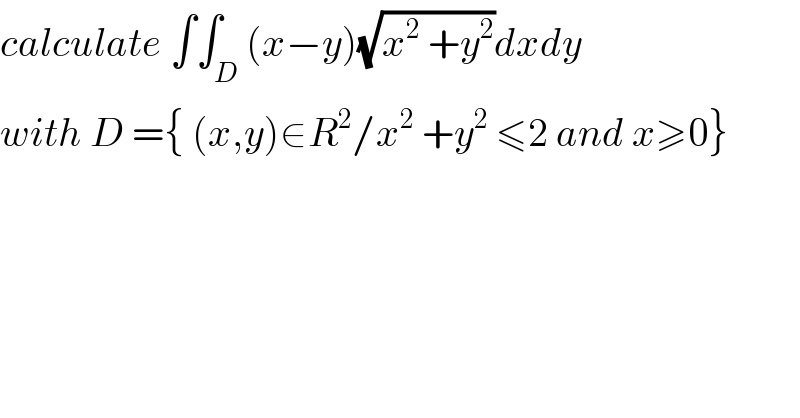
$${calculate}\:\int\int_{{D}} \left({x}−{y}\right)\sqrt{{x}^{\mathrm{2}} \:+{y}^{\mathrm{2}} }{dxdy} \\ $$$${with}\:{D}\:=\left\{\:\left({x},{y}\right)\in{R}^{\mathrm{2}} /{x}^{\mathrm{2}} \:+{y}^{\mathrm{2}} \:\leqslant\mathrm{2}\:{and}\:{x}\geqslant\mathrm{0}\right\} \\ $$
Commented by maxmathsup by imad last updated on 02/Apr/19
![let use the diffeomorphism x=rcosθ and y =rsinθ we have x^2 +y^2 ≤2 ⇒r^2 ≤2 ⇒ 0≤r≤(√2) and x≥0 ⇒−(π/2) ≤θ≤(π/2) ∫∫_D (x−y)(√(x^2 +y^2 ))dxdy = ∫∫_(0≤r≤(√2) and −(π/2)≤θ≤(π/2)) (rcosθ −rsinθ)r rdrdθ =∫_0 ^(√2) r^3 dr .∫_(−(π/2)) ^(π/2) (cosθ −sinθ)dθ but ∫_0 ^(√2) r^3 dr =[(r^4 /4)]_0 ^(√2) =1 ∫_(−(π/2)) ^(π/2) (cosθ −sinθ)dθ =[sinθ +cosθ]_(−(π/2)) ^(π/2) =1 −(−1) =2 ⇒ ∫∫_D (x−y)(√(x^2 +y^2 ))dxdy = 2 .](https://www.tinkutara.com/question/Q57340.png)
$${let}\:{use}\:{the}\:{diffeomorphism}\:\:\:{x}={rcos}\theta\:\:{and}\:{y}\:={rsin}\theta \\ $$$${we}\:{have}\:{x}^{\mathrm{2}} \:+{y}^{\mathrm{2}} \:\leqslant\mathrm{2}\:\Rightarrow{r}^{\mathrm{2}} \:\leqslant\mathrm{2}\:\Rightarrow\:\mathrm{0}\leqslant{r}\leqslant\sqrt{\mathrm{2}}\:\:\:\:{and}\:{x}\geqslant\mathrm{0}\:\Rightarrow−\frac{\pi}{\mathrm{2}}\:\leqslant\theta\leqslant\frac{\pi}{\mathrm{2}} \\ $$$$\int\int_{{D}} \left({x}−{y}\right)\sqrt{{x}^{\mathrm{2}} \:+{y}^{\mathrm{2}} }{dxdy}\:=\:\int\int_{\mathrm{0}\leqslant{r}\leqslant\sqrt{\mathrm{2}}\:\:{and}\:−\frac{\pi}{\mathrm{2}}\leqslant\theta\leqslant\frac{\pi}{\mathrm{2}}} \left({rcos}\theta\:−{rsin}\theta\right){r}\:{rdrd}\theta \\ $$$$=\int_{\mathrm{0}} ^{\sqrt{\mathrm{2}}} {r}^{\mathrm{3}} {dr}\:.\int_{−\frac{\pi}{\mathrm{2}}} ^{\frac{\pi}{\mathrm{2}}} \:\left({cos}\theta\:−{sin}\theta\right){d}\theta\:\:\:{but}\:\int_{\mathrm{0}} ^{\sqrt{\mathrm{2}}} \:{r}^{\mathrm{3}} {dr}\:=\left[\frac{{r}^{\mathrm{4}} }{\mathrm{4}}\right]_{\mathrm{0}} ^{\sqrt{\mathrm{2}}} =\mathrm{1} \\ $$$$\int_{−\frac{\pi}{\mathrm{2}}} ^{\frac{\pi}{\mathrm{2}}} \:\left({cos}\theta\:−{sin}\theta\right){d}\theta\:=\left[{sin}\theta\:+{cos}\theta\right]_{−\frac{\pi}{\mathrm{2}}} ^{\frac{\pi}{\mathrm{2}}} \:=\mathrm{1}\:−\left(−\mathrm{1}\right)\:=\mathrm{2}\:\Rightarrow \\ $$$$\int\int_{{D}} \left({x}−{y}\right)\sqrt{{x}^{\mathrm{2}} \:+{y}^{\mathrm{2}} }{dxdy}\:=\:\mathrm{2}\:. \\ $$
Answered by kaivan.ahmadi last updated on 03/Apr/19
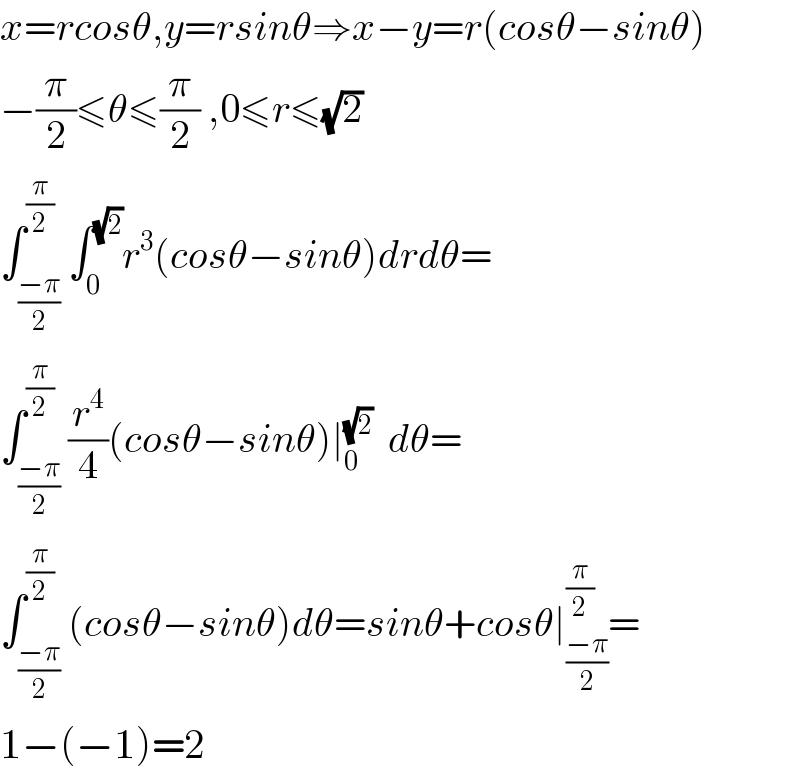
$${x}={rcos}\theta,{y}={rsin}\theta\Rightarrow{x}−{y}={r}\left({cos}\theta−{sin}\theta\right) \\ $$$$−\frac{\pi}{\mathrm{2}}\leqslant\theta\leqslant\frac{\pi}{\mathrm{2}}\:,\mathrm{0}\leqslant{r}\leqslant\sqrt{\mathrm{2}} \\ $$$$\int_{\frac{−\pi}{\mathrm{2}}} ^{\frac{\pi}{\mathrm{2}}} \int_{\mathrm{0}} ^{\sqrt{\mathrm{2}}} {r}^{\mathrm{3}} \left({cos}\theta−{sin}\theta\right){drd}\theta= \\ $$$$\int_{\frac{−\pi}{\mathrm{2}}} ^{\frac{\pi}{\mathrm{2}}} \frac{{r}^{\mathrm{4}} }{\mathrm{4}}\left({cos}\theta−{sin}\theta\right)\mid_{\mathrm{0}} ^{\sqrt{\mathrm{2}}} \:\:{d}\theta= \\ $$$$\int_{\frac{−\pi}{\mathrm{2}}} ^{\frac{\pi}{\mathrm{2}}} \left({cos}\theta−{sin}\theta\right){d}\theta={sin}\theta+{cos}\theta\mid_{\frac{−\pi}{\mathrm{2}}} ^{\frac{\pi}{\mathrm{2}}} = \\ $$$$\mathrm{1}−\left(−\mathrm{1}\right)=\mathrm{2} \\ $$
