Question Number 89312 by abdomathmax last updated on 16/Apr/20
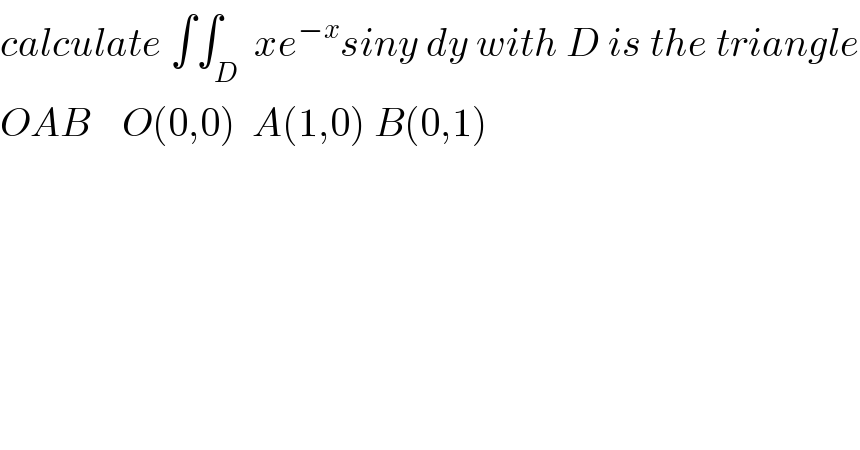
$${calculate}\:\int\int_{{D}} \:{xe}^{−{x}} {siny}\:{dy}\:{with}\:{D}\:{is}\:{the}\:{triangle} \\ $$$${OAB}\:\:\:\:{O}\left(\mathrm{0},\mathrm{0}\right)\:\:{A}\left(\mathrm{1},\mathrm{0}\right)\:{B}\left(\mathrm{0},\mathrm{1}\right) \\ $$
Commented by mathmax by abdo last updated on 17/Apr/20
![the equation of line (AB) is x+y =1 ⇒y =1−x ⇒ ∫∫_D xe^(−x) siny dxdy =∫_0 ^1 (∫_0 ^(1−x) sinydy)xe^(−x) dx we have ∫_0 ^(1−x) siny dy =[−cosy]_0 ^(1−x) =1−cos(1−x) ⇒ I =∫_0 ^1 (1−cos(1−x))xe^(−x) dx =∫_0 ^1 xe^(−x) dx−∫_0 ^1 xe^(−x) cos(1−x)dx but ∫_0 ^1 xe^(−x) dx =[−xe^(−x) ]_0 ^1 +∫_0 ^1 e^(−x) dx =−e^(−1) +[−e^(−x) ]_0 ^1 =−e^(−1) +1−e^(−1) =1−2e^(−1) ∫_0 ^1 xe^(−x) cos(1−x)dx =Re(∫_0 ^1 xe^(−x) e^(i(1−x)) dx) ∫_0 ^1 xe^(−x+i−ix) ex =e^i ∫_0 ^1 x e^(−(1+i)x) dx =e^i { [ (x/(−(1+i))) e^(−(1+i)x) ]_0 ^1 −∫_0 ^1 (1/(−(1+i)))e^(−(1+i)x) dx} =e^i {−(1/((1+i)))(e^(−(1+i)) −1)+(1/(1+i))[−(1/(1+i))e^(−(1+i)x) ]_0 ^1 } =−(e^i /(1+i))(e^(−(1+i)) −1)−(e^i /((1+i)^2 ))(e^(−(1+i)) −1) =−(((1−i))/2)(e^(−1) −e^i )−((e^(−1) −e^i )/(2i)) =((e^i −e^(−1) )/2)(1−i +(1/i)) =((e^i −e^(−1) )/2)(1−2i) =(1/2)(1−2i)(cos(1)+isin(1)−e^(−1) ) =(1/2){cos(1)+isin(1)−e^(−1) −2icos(1)+2sin(1)+2ie^(−1) } ⇒ ∫_0 ^1 x e^(−x) cos(1−x)dx =((cos(1)+2sin(1)−e^(−1) )/2) ⇒ I =1−2e^(−1) −(1/2){cos(1)+2sin(1)−e^(−1) }](https://www.tinkutara.com/question/Q89450.png)
$${the}\:{equation}\:{of}\:{line}\:\left({AB}\right)\:{is}\:{x}+{y}\:=\mathrm{1}\:\Rightarrow{y}\:=\mathrm{1}−{x}\:\Rightarrow \\ $$$$\int\int_{{D}} {xe}^{−{x}} \:{siny}\:{dxdy}\:=\int_{\mathrm{0}} ^{\mathrm{1}} \left(\int_{\mathrm{0}} ^{\mathrm{1}−{x}} {sinydy}\right){xe}^{−{x}} \:{dx} \\ $$$${we}\:{have}\:\int_{\mathrm{0}} ^{\mathrm{1}−{x}} \:{siny}\:{dy}\:=\left[−{cosy}\right]_{\mathrm{0}} ^{\mathrm{1}−{x}} =\mathrm{1}−{cos}\left(\mathrm{1}−{x}\right)\:\Rightarrow \\ $$$${I}\:=\int_{\mathrm{0}} ^{\mathrm{1}} \left(\mathrm{1}−{cos}\left(\mathrm{1}−{x}\right)\right){xe}^{−{x}} \:{dx} \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{1}} \:{xe}^{−{x}} \:{dx}−\int_{\mathrm{0}} ^{\mathrm{1}} \:{xe}^{−{x}} \:{cos}\left(\mathrm{1}−{x}\right){dx}\:\:{but} \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \:{xe}^{−{x}} \:{dx}\:=\left[−{xe}^{−{x}} \right]_{\mathrm{0}} ^{\mathrm{1}} \:+\int_{\mathrm{0}} ^{\mathrm{1}} \:{e}^{−{x}} \:{dx}\:=−{e}^{−\mathrm{1}} \:+\left[−{e}^{−{x}} \right]_{\mathrm{0}} ^{\mathrm{1}} \\ $$$$=−{e}^{−\mathrm{1}} +\mathrm{1}−{e}^{−\mathrm{1}} \:=\mathrm{1}−\mathrm{2}{e}^{−\mathrm{1}} \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \:{xe}^{−{x}} \:{cos}\left(\mathrm{1}−{x}\right){dx}\:={Re}\left(\int_{\mathrm{0}} ^{\mathrm{1}} \:{xe}^{−{x}} {e}^{{i}\left(\mathrm{1}−{x}\right)} \:{dx}\right) \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \:{xe}^{−{x}+{i}−{ix}} \:{ex}\:={e}^{{i}} \int_{\mathrm{0}} ^{\mathrm{1}} \:{x}\:{e}^{−\left(\mathrm{1}+{i}\right){x}} \:{dx} \\ $$$$={e}^{{i}} \left\{\:\:\left[\:\frac{{x}}{−\left(\mathrm{1}+{i}\right)}\:{e}^{−\left(\mathrm{1}+{i}\right){x}} \right]_{\mathrm{0}} ^{\mathrm{1}} \:−\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{1}}{−\left(\mathrm{1}+{i}\right)}{e}^{−\left(\mathrm{1}+{i}\right){x}} {dx}\right\} \\ $$$$={e}^{{i}} \left\{−\frac{\mathrm{1}}{\left(\mathrm{1}+{i}\right)}\left({e}^{−\left(\mathrm{1}+{i}\right)} −\mathrm{1}\right)+\frac{\mathrm{1}}{\mathrm{1}+{i}}\left[−\frac{\mathrm{1}}{\mathrm{1}+{i}}{e}^{−\left(\mathrm{1}+{i}\right){x}} \right]_{\mathrm{0}} ^{\mathrm{1}} \right\} \\ $$$$=−\frac{{e}^{{i}} }{\mathrm{1}+{i}}\left({e}^{−\left(\mathrm{1}+{i}\right)} −\mathrm{1}\right)−\frac{{e}^{{i}} }{\left(\mathrm{1}+{i}\right)^{\mathrm{2}} }\left({e}^{−\left(\mathrm{1}+{i}\right)} −\mathrm{1}\right) \\ $$$$=−\frac{\left(\mathrm{1}−{i}\right)}{\mathrm{2}}\left({e}^{−\mathrm{1}} −{e}^{{i}} \right)−\frac{{e}^{−\mathrm{1}} −{e}^{{i}} }{\mathrm{2}{i}} \\ $$$$=\frac{{e}^{{i}} −{e}^{−\mathrm{1}} }{\mathrm{2}}\left(\mathrm{1}−{i}\:+\frac{\mathrm{1}}{{i}}\right)\:=\frac{{e}^{{i}} −{e}^{−\mathrm{1}} }{\mathrm{2}}\left(\mathrm{1}−\mathrm{2}{i}\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{1}−\mathrm{2}{i}\right)\left({cos}\left(\mathrm{1}\right)+{isin}\left(\mathrm{1}\right)−{e}^{−\mathrm{1}} \right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\left\{{cos}\left(\mathrm{1}\right)+{isin}\left(\mathrm{1}\right)−{e}^{−\mathrm{1}} −\mathrm{2}{icos}\left(\mathrm{1}\right)+\mathrm{2}{sin}\left(\mathrm{1}\right)+\mathrm{2}{ie}^{−\mathrm{1}} \right\}\:\Rightarrow \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \:{x}\:{e}^{−{x}} \:{cos}\left(\mathrm{1}−{x}\right){dx}\:=\frac{{cos}\left(\mathrm{1}\right)+\mathrm{2}{sin}\left(\mathrm{1}\right)−{e}^{−\mathrm{1}} }{\mathrm{2}}\:\Rightarrow \\ $$$${I}\:=\mathrm{1}−\mathrm{2}{e}^{−\mathrm{1}} −\frac{\mathrm{1}}{\mathrm{2}}\left\{{cos}\left(\mathrm{1}\right)+\mathrm{2}{sin}\left(\mathrm{1}\right)−{e}^{−\mathrm{1}} \right\} \\ $$
