Question Number 42503 by maxmathsup by imad last updated on 26/Aug/18
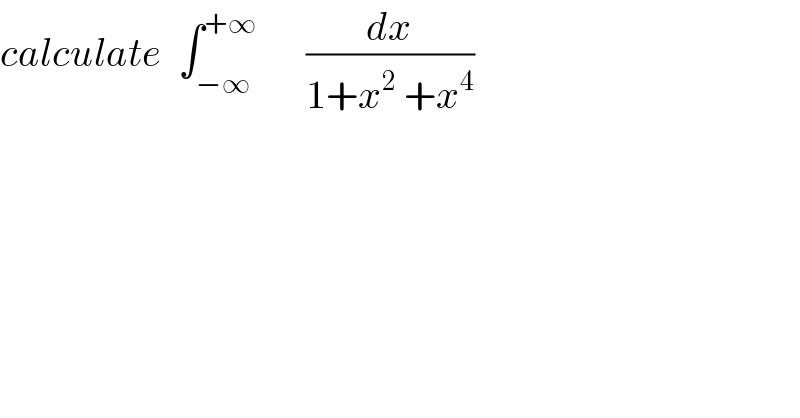
$${calculate}\:\:\int_{−\infty} ^{+\infty} \:\:\:\:\:\:\frac{{dx}}{\mathrm{1}+{x}^{\mathrm{2}} \:+{x}^{\mathrm{4}} } \\ $$
Commented by maxmathsup by imad last updated on 27/Aug/18

$${method}\:{of}\:{residus}\:{let}\:\varphi\left({z}\right)\:=\frac{\mathrm{1}}{{z}^{\mathrm{4}} \:+{z}^{\mathrm{2}} \:+\mathrm{1}}\:\:.{roots}\:{of}\:{z}^{\mathrm{4}} \:+{z}^{\mathrm{2}} \:+\mathrm{1}\:=\mathrm{0} \\ $$$${z}^{\mathrm{2}} ={t}\:\Rightarrow{t}^{\mathrm{2}} \:+{t}\:+\mathrm{1}\:=\mathrm{0}\:\Delta\:=\mathrm{1}−\mathrm{4}=−\mathrm{3}=\left({i}\sqrt{\mathrm{3}}\right)^{\mathrm{2}} \:\Rightarrow{t}_{\mathrm{1}} =\frac{−\mathrm{1}+{i}\sqrt{\mathrm{3}}}{\mathrm{2}}\:={e}^{{i}\frac{\mathrm{2}\pi}{\mathrm{3}}} \:\:\:\left(={j}\right) \\ $$$${t}_{\mathrm{2}} =\frac{−\mathrm{1}−{i}\sqrt{\mathrm{3}}}{\mathrm{2}}\:={e}^{−\frac{{i}\mathrm{2}\pi}{\mathrm{2}}} \:\:\Rightarrow\:{z}^{\mathrm{2}} \:={e}^{\frac{{i}\mathrm{2}\pi}{\mathrm{3}}} \:\Rightarrow\:{z}\:=\overset{−} {+}\:{e}^{\frac{{i}\pi}{\mathrm{3}}} \:\:{and}\:{z}_{\mathrm{2}} ={e}^{−\frac{{i}\mathrm{2}\pi}{\mathrm{3}}} \:\Rightarrow{z}\:=\overset{−} {+}{e}^{−\frac{{i}\pi}{\mathrm{3}}} \\ $$$$\Rightarrow\varphi\left({z}\right)\:=\:\frac{\mathrm{1}}{\left({z}−{e}^{\frac{{i}\pi}{\mathrm{3}}} \right)\left({z}+{e}^{\frac{{i}\pi}{\mathrm{3}}} \right)\left({z}−{e}^{−\frac{{i}\pi}{\mathrm{3}}} \right)\left({z}\:+{e}^{−\frac{{i}\pi}{\mathrm{3}}} \right)}\:\Rightarrow \\ $$$$\int_{−\infty} ^{+\infty} \:\:\varphi\left({z}\right){dz}\:=\mathrm{2}{i}\pi\:\left\{\:{Res}\left(\varphi,{e}^{\frac{{i}\pi}{\mathrm{3}}} \right)\:+{Res}\left(\varphi,−{e}^{−\frac{{i}\pi}{\mathrm{3}}} \right)\right\}\:\:{but}\:\: \\ $$$${Res}\left(\varphi,\:{e}^{\frac{{i}\pi}{\mathrm{3}}} \right)\:={lim}_{{z}\rightarrow{e}^{\frac{{i}\pi}{\mathrm{3}}} } \:\:\:\left({z}−{e}^{\frac{{i}\pi}{\mathrm{3}}} \right)\varphi\left({z}\right)\:=\:\frac{\mathrm{1}}{\mathrm{2}\:{e}^{\frac{{i}\pi}{\mathrm{3}}} \:\left(\mathrm{2}{i}\:{sin}\left(\frac{\pi}{\mathrm{3}}\right)\right)\left(\mathrm{2}{cos}\left(\frac{\pi}{\mathrm{3}}\right)\right)} \\ $$$$=\:\:\:\frac{{e}^{−\frac{{i}\pi}{\mathrm{3}}} }{\mathrm{8}{i}\:\frac{\sqrt{\mathrm{3}}}{\mathrm{2}\:}\:\frac{\mathrm{1}}{\mathrm{2}}}\:=\:\:\frac{{e}^{−\frac{{i}\pi}{\mathrm{3}}} }{\mathrm{4}{i}\sqrt{\mathrm{3}}} \\ $$$${Res}\left(\varphi,\:−{e}^{−\frac{{i}\pi}{\mathrm{3}}} \right)\:={lim}_{{z}\rightarrow−{e}^{−\frac{{i}\pi}{\mathrm{3}}} } \:\:\:\:\left({z}+{e}^{−\frac{{i}\pi}{\mathrm{3}}} \right)\varphi\left({z}\right)\:=\:\frac{\mathrm{1}}{\left(−\mathrm{2}{isin}\left(\frac{\pi}{\mathrm{3}}\right)\left(\mathrm{2}{cos}\left(\frac{\pi}{\mathrm{3}}\right)\right)\left(−\mathrm{2}{e}^{−\frac{{i}\pi}{\mathrm{3}}} \right)\right.} \\ $$$$=\:\:\frac{{e}^{\frac{{i}\pi}{\mathrm{3}}} }{\mathrm{4}{i}\sqrt{\mathrm{3}}}\:\Rightarrow\int_{−\infty} ^{+\infty} \:\varphi\left({z}\right){dz}\:=\mathrm{2}{i}\pi\frac{\mathrm{1}}{\mathrm{4}{i}\sqrt{\mathrm{3}}}\left\{\:{e}^{−\frac{{i}\pi}{\mathrm{3}}} \:+{e}^{\frac{{i}\pi}{\mathrm{3}}} \right\} \\ $$$$=\:\frac{\pi}{\mathrm{2}\sqrt{\mathrm{3}}}\:\mathrm{2}\:{cos}\left(\frac{\pi}{\mathrm{3}}\right)\:=\frac{\pi}{\mathrm{2}\sqrt{\mathrm{3}}}\left(\mathrm{1}\right)\:\Rightarrow\:\int_{−\infty} ^{+\infty} \:\:\:\frac{{dx}}{\mathrm{1}+{x}^{\mathrm{2}} \:+{x}^{\mathrm{4}} }\:=\:\frac{\pi}{\mathrm{2}\sqrt{\mathrm{3}}}\:. \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 27/Aug/18
![∫_(−∞) ^∞ ((1/x^2 )/(x^2 +(1/x^2 )+1))dx (1/2)∫_(−∞) ^∞ ((1+(1/x^2 )−(1−(1/x^2 )))/(x^2 +(1/x^2 )+1))dx (1/2)[∫_(−∞) ^∞ ((d(x−(1/x)))/((x−(1/x))^2 +3))−∫_(−∞) ^∞ ((d(x+(1/x)))/((x+(1/x))^2 −1))] (1/2)[∣(1/( (√3)))tan^(−1) (((x−(1/x))/( (√3))))∣_(−∞) ^∞ −(1/(2×1))∣ln(((x+(1/x)−1)/(x+(1/x)+1)))∣_(−∞) ^∞ ] =(1/2)[(1/( (√3)))((Π/2)+(Π/2))−(1/(2 )){ln(((∞−1)/(∞+1)))−ln∣(((−∞−1)/(−∞+2)))∣] (1/2)[(Π/( (√3)))−(1/2){ln(((1−0)/(1+0)))−ln∣(((∞+1)/(2−∞)))∣}] (1/2)[(Π/( (√3)))−(1/2){0−ln∣((1+(1/∞))/((2/∞)−1))∣}] (1/2)×(Π/( (√3)))−(1/2)(0−0) (Π/(2(√3)))](https://www.tinkutara.com/question/Q42572.png)
$$\int_{−\infty} ^{\infty} \frac{\frac{\mathrm{1}}{{x}^{\mathrm{2}} }}{{x}^{\mathrm{2}} +\frac{\mathrm{1}}{{x}^{\mathrm{2}} }+\mathrm{1}}{dx} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}\int_{−\infty} ^{\infty} \frac{\mathrm{1}+\frac{\mathrm{1}}{{x}^{\mathrm{2}} }−\left(\mathrm{1}−\frac{\mathrm{1}}{{x}^{\mathrm{2}} }\right)}{{x}^{\mathrm{2}} +\frac{\mathrm{1}}{{x}^{\mathrm{2}} }+\mathrm{1}}{dx} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}\left[\int_{−\infty} ^{\infty} \frac{{d}\left({x}−\frac{\mathrm{1}}{{x}}\right)}{\left({x}−\frac{\mathrm{1}}{{x}}\right)^{\mathrm{2}} +\mathrm{3}}−\int_{−\infty} ^{\infty} \frac{{d}\left({x}+\frac{\mathrm{1}}{{x}}\right)}{\left({x}+\frac{\mathrm{1}}{{x}}\right)^{\mathrm{2}} −\mathrm{1}}\right] \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}\left[\mid\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}{tan}^{−\mathrm{1}} \left(\frac{{x}−\frac{\mathrm{1}}{{x}}}{\:\sqrt{\mathrm{3}}}\right)\mid_{−\infty} ^{\infty} −\frac{\mathrm{1}}{\mathrm{2}×\mathrm{1}}\mid{ln}\left(\frac{{x}+\frac{\mathrm{1}}{{x}}−\mathrm{1}}{{x}+\frac{\mathrm{1}}{{x}}+\mathrm{1}}\right)\mid_{−\infty} ^{\infty} \right] \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\left[\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}\left(\frac{\Pi}{\mathrm{2}}+\frac{\Pi}{\mathrm{2}}\right)−\frac{\mathrm{1}}{\mathrm{2}\:}\left\{{ln}\left(\frac{\infty−\mathrm{1}}{\infty+\mathrm{1}}\right)−{ln}\mid\left(\frac{−\infty−\mathrm{1}}{−\infty+\mathrm{2}}\right)\mid\right]\right. \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}\left[\frac{\Pi}{\:\sqrt{\mathrm{3}}}−\frac{\mathrm{1}}{\mathrm{2}}\left\{{ln}\left(\frac{\mathrm{1}−\mathrm{0}}{\mathrm{1}+\mathrm{0}}\right)−{ln}\mid\left(\frac{\infty+\mathrm{1}}{\mathrm{2}−\infty}\right)\mid\right\}\right] \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}\left[\frac{\Pi}{\:\sqrt{\mathrm{3}}}−\frac{\mathrm{1}}{\mathrm{2}}\left\{\mathrm{0}−{ln}\mid\frac{\mathrm{1}+\frac{\mathrm{1}}{\infty}}{\frac{\mathrm{2}}{\infty}−\mathrm{1}}\mid\right\}\right] \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}×\frac{\Pi}{\:\sqrt{\mathrm{3}}}−\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{0}−\mathrm{0}\right) \\ $$$$\frac{\Pi}{\mathrm{2}\sqrt{\mathrm{3}}} \\ $$$$ \\ $$
