Menu Close

calculate-dx-1-x-x-2-3-

Tinku Tara 0 Comments
Pin




Question Number 35055 by math khazana by abdo last updated on 14/May/18
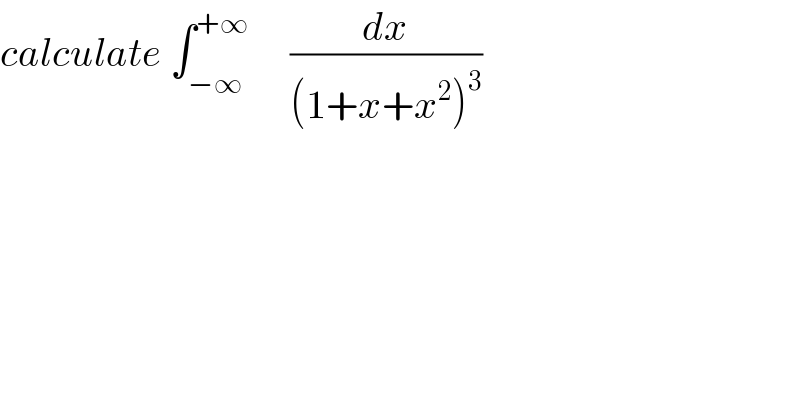
calculate ∫_(−∞) ^(+∞) (dx/((1+x+x^2 )^3 ))
$${calculate}\:\int_{−\infty} ^{+\infty} \:\:\:\:\:\frac{{dx}}{\left(\mathrm{1}+{x}+{x}^{\mathrm{2}} \right)^{\mathrm{3}} } \\ $$
Commented by math khazana by abdo last updated on 15/May/18
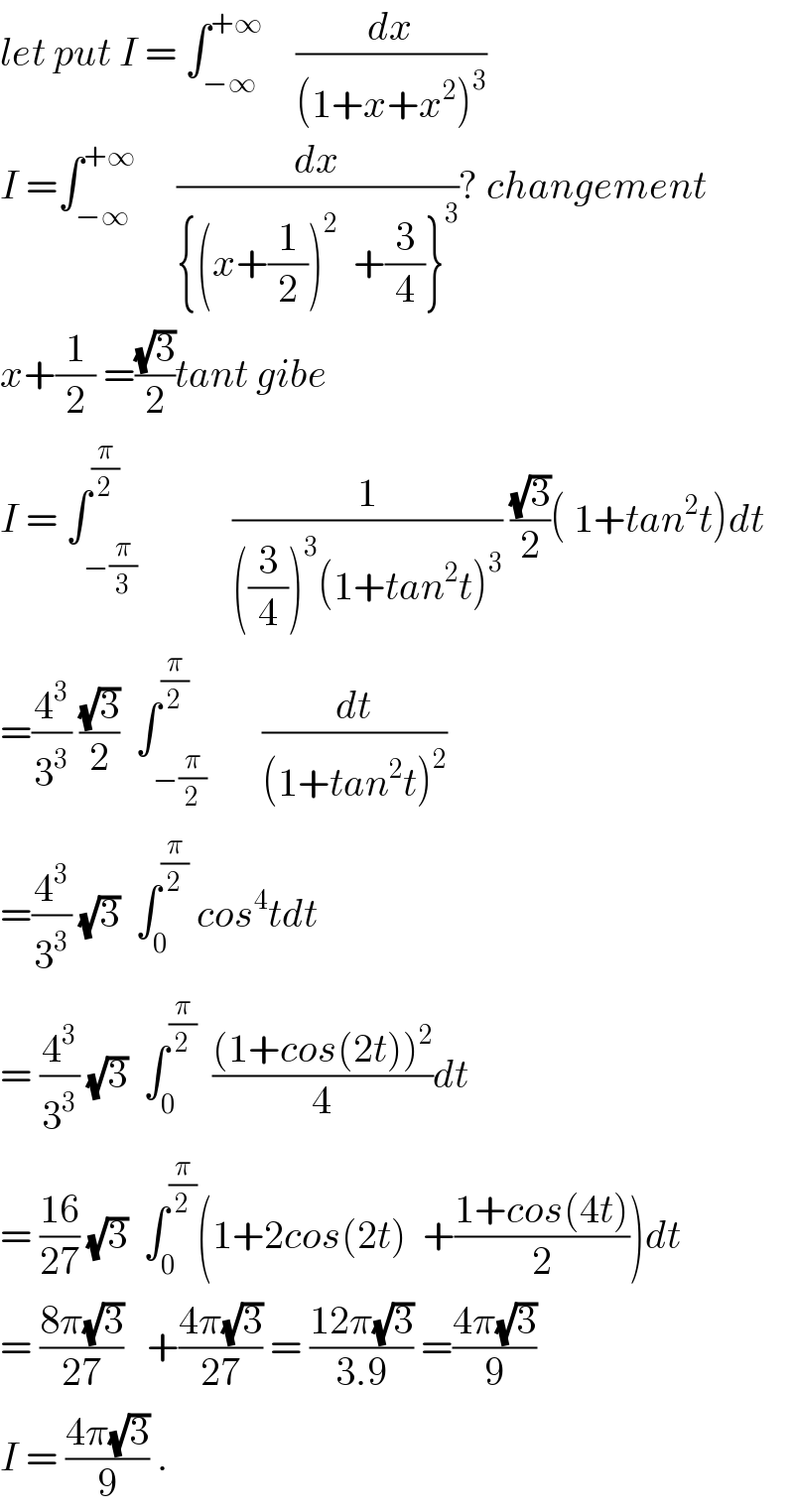
let put I = ∫_(−∞) ^(+∞) (dx/((1+x+x^2 )^3 )) I =∫_(−∞) ^(+∞) (dx/({(x+(1/2))^2 +(3/4)}^3 ))? changement x+(1/2) =((√3)/2)tant gibe I = ∫_(−(π/3)) ^(π/2) (1/(((3/4))^3 (1+tan^2 t)^3 )) ((√3)/2)( 1+tan^2 t)dt =(4^3 /3^3 ) ((√3)/2) ∫_(−(π/2)) ^(π/2) (dt/((1+tan^2 t)^2 )) =(4^3 /3^3 ) (√3) ∫_0 ^(π/2) cos^4 tdt = (4^3 /3^3 ) (√3) ∫_0 ^(π/2) (((1+cos(2t))^2 )/4)dt = ((16)/(27)) (√3) ∫_0 ^(π/2) (1+2cos(2t) +((1+cos(4t))/2))dt = ((8π(√3))/(27)) +((4π(√3))/(27)) = ((12π(√3))/(3.9)) =((4π(√3))/9) I = ((4π(√3))/9) .
$${let}\:{put}\:{I}\:=\:\int_{−\infty} ^{+\infty} \:\:\:\:\frac{{dx}}{\left(\mathrm{1}+{x}+{x}^{\mathrm{2}} \right)^{\mathrm{3}} } \\ $$$${I}\:=\int_{−\infty} ^{+\infty} \:\:\:\:\:\frac{{dx}}{\left\{\left({x}+\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} \:\:+\frac{\mathrm{3}}{\mathrm{4}}\right\}^{\mathrm{3}} }?\:{changement} \\ $$$${x}+\frac{\mathrm{1}}{\mathrm{2}}\:=\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}{tant}\:{gibe} \\ $$$${I}\:=\:\int_{−\frac{\pi}{\mathrm{3}}} ^{\frac{\pi}{\mathrm{2}}} \:\:\:\:\:\:\:\:\:\:\:\frac{\mathrm{1}}{\left(\frac{\mathrm{3}}{\mathrm{4}}\right)^{\mathrm{3}} \left(\mathrm{1}+{tan}^{\mathrm{2}} {t}\right)^{\mathrm{3}} }\:\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\left(\:\mathrm{1}+{tan}^{\mathrm{2}} {t}\right){dt} \\ $$$$=\frac{\mathrm{4}^{\mathrm{3}} }{\mathrm{3}^{\mathrm{3}} }\:\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\:\:\int_{−\frac{\pi}{\mathrm{2}}} ^{\frac{\pi}{\mathrm{2}}} \:\:\:\:\:\:\frac{{dt}}{\left(\mathrm{1}+{tan}^{\mathrm{2}} {t}\right)^{\mathrm{2}} } \\ $$$$=\frac{\mathrm{4}^{\mathrm{3}} }{\mathrm{3}^{\mathrm{3}} }\:\sqrt{\mathrm{3}}\:\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:{cos}^{\mathrm{4}} {tdt} \\ $$$$=\:\frac{\mathrm{4}^{\mathrm{3}} }{\mathrm{3}^{\mathrm{3}} }\:\sqrt{\mathrm{3}}\:\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\:\frac{\left(\mathrm{1}+{cos}\left(\mathrm{2}{t}\right)\right)^{\mathrm{2}} }{\mathrm{4}}{dt} \\ $$$$=\:\frac{\mathrm{16}}{\mathrm{27}}\:\sqrt{\mathrm{3}}\:\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \left(\mathrm{1}+\mathrm{2}{cos}\left(\mathrm{2}{t}\right)\:\:+\frac{\mathrm{1}+{cos}\left(\mathrm{4}{t}\right)}{\mathrm{2}}\right){dt} \\ $$$$=\:\frac{\mathrm{8}\pi\sqrt{\mathrm{3}}}{\mathrm{27}}\:\:\:+\frac{\mathrm{4}\pi\sqrt{\mathrm{3}}}{\mathrm{27}}\:=\:\frac{\mathrm{12}\pi\sqrt{\mathrm{3}}}{\mathrm{3}.\mathrm{9}}\:=\frac{\mathrm{4}\pi\sqrt{\mathrm{3}}}{\mathrm{9}} \\ $$$${I}\:=\:\frac{\mathrm{4}\pi\sqrt{\mathrm{3}}}{\mathrm{9}}\:. \\ $$
Commented by abdo imad last updated on 17/May/18
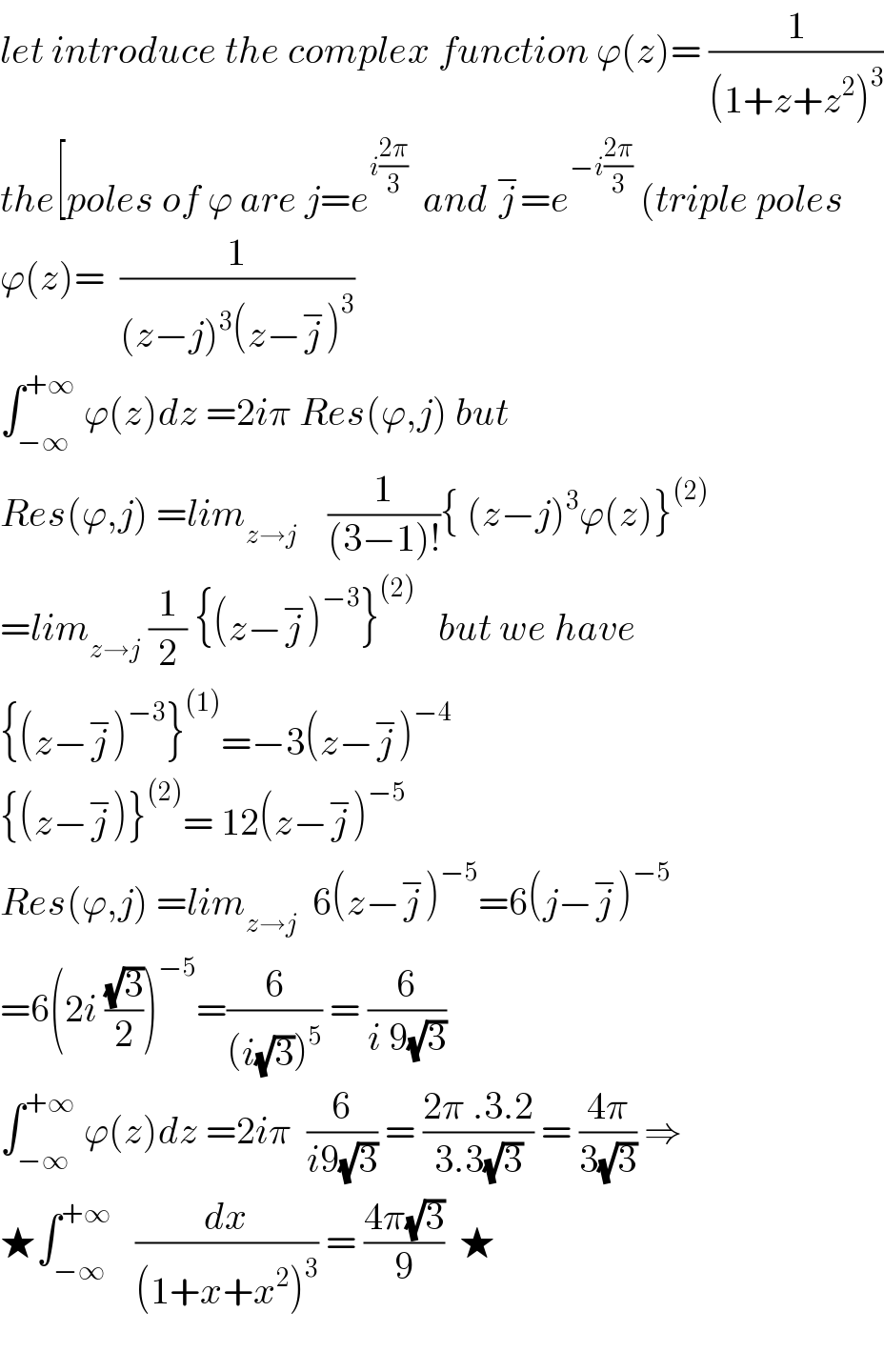
let introduce the complex function ϕ(z)= (1/((1+z+z^2 )^3 )) the[poles of ϕ are j=e^(i((2π)/3)) and j^− =e^(−i((2π)/3)) (triple poles ϕ(z)= (1/((z−j)^3 (z−j^− )^3 )) ∫_(−∞) ^(+∞) ϕ(z)dz =2iπ Res(ϕ,j) but Res(ϕ,j) =lim_(z→j) (1/((3−1)!)){ (z−j)^3 ϕ(z)}^((2)) =lim_(z→j) (1/2) {(z−j^− )^(−3) }^((2)) but we have {(z−j^− )^(−3) }^((1)) =−3(z−j^− )^(−4) {(z−j^− )}^((2)) = 12(z−j^− )^(−5) Res(ϕ,j) =lim_(z→j) 6(z−j^− )^(−5) =6(j−j^− )^(−5) =6(2i ((√3)/2))^(−5) =(6/((i(√3))^5 )) = (6/(i 9(√3))) ∫_(−∞) ^(+∞) ϕ(z)dz =2iπ (6/(i9(√3))) = ((2π .3.2)/(3.3(√3))) = ((4π)/(3(√3))) ⇒ ★∫_(−∞) ^(+∞) (dx/((1+x+x^2 )^3 )) = ((4π(√3))/9) ★
$${let}\:{introduce}\:{the}\:{complex}\:{function}\:\varphi\left({z}\right)=\:\frac{\mathrm{1}}{\left(\mathrm{1}+{z}+{z}^{\mathrm{2}} \right)^{\mathrm{3}} } \\ $$$${the}\left[{poles}\:{of}\:\varphi\:{are}\:{j}={e}^{{i}\frac{\mathrm{2}\pi}{\mathrm{3}}} \:\:{and}\:\overset{−} {{j}}={e}^{−{i}\frac{\mathrm{2}\pi}{\mathrm{3}}} \:\left({triple}\:{poles}\right.\right. \\ $$$$\varphi\left({z}\right)=\:\:\frac{\mathrm{1}}{\left({z}−{j}\right)^{\mathrm{3}} \left({z}−\overset{−} {{j}}\right)^{\mathrm{3}} } \\ $$$$\int_{−\infty} ^{+\infty} \:\varphi\left({z}\right){dz}\:=\mathrm{2}{i}\pi\:{Res}\left(\varphi,{j}\right)\:{but}\: \\ $$$${Res}\left(\varphi,{j}\right)\:={lim}_{{z}\rightarrow{j}} \:\:\:\:\frac{\mathrm{1}}{\left(\mathrm{3}−\mathrm{1}\right)!}\left\{\:\left({z}−{j}\right)^{\mathrm{3}} \varphi\left({z}\right)\right\}^{\left(\mathrm{2}\right)} \\ $$$$={lim}_{{z}\rightarrow{j}} \:\frac{\mathrm{1}}{\mathrm{2}}\:\left\{\left({z}−\overset{−} {{j}}\right)^{−\mathrm{3}} \right\}^{\left(\mathrm{2}\right)} \:\:\:{but}\:{we}\:{have} \\ $$$$\left\{\left({z}−\overset{−} {{j}}\right)^{−\mathrm{3}} \right\}^{\left(\mathrm{1}\right)} =−\mathrm{3}\left({z}−\overset{−} {{j}}\right)^{−\mathrm{4}} \\ $$$$\left\{\left({z}−\overset{−} {{j}}\right)\right\}^{\left(\mathrm{2}\right)} =\:\mathrm{12}\left({z}−\overset{−} {{j}}\right)^{−\mathrm{5}} \\ $$$${Res}\left(\varphi,{j}\right)\:={lim}_{{z}\rightarrow{j}} \:\:\mathrm{6}\left({z}−\overset{−} {{j}}\right)^{−\mathrm{5}} =\mathrm{6}\left({j}−\overset{−} {{j}}\right)^{−\mathrm{5}} \\ $$$$=\mathrm{6}\left(\mathrm{2}{i}\:\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\right)^{−\mathrm{5}} =\frac{\mathrm{6}}{\left({i}\sqrt{\mathrm{3}}\right)^{\mathrm{5}} }\:=\:\frac{\mathrm{6}}{{i}\:\mathrm{9}\sqrt{\mathrm{3}}} \\ $$$$\int_{−\infty} ^{+\infty} \:\varphi\left({z}\right){dz}\:=\mathrm{2}{i}\pi\:\:\frac{\mathrm{6}}{{i}\mathrm{9}\sqrt{\mathrm{3}}}\:=\:\frac{\mathrm{2}\pi\:.\mathrm{3}.\mathrm{2}}{\mathrm{3}.\mathrm{3}\sqrt{\mathrm{3}}}\:=\:\frac{\mathrm{4}\pi}{\mathrm{3}\sqrt{\mathrm{3}}}\:\Rightarrow \\ $$$$\bigstar\int_{−\infty} ^{+\infty} \:\:\:\frac{{dx}}{\left(\mathrm{1}+{x}+{x}^{\mathrm{2}} \right)^{\mathrm{3}} }\:=\:\frac{\mathrm{4}\pi\sqrt{\mathrm{3}}}{\mathrm{9}}\:\:\bigstar \\ $$$$ \\ $$
Answered by MJS last updated on 15/May/18
∫(dx/((x^2 +x+1)^3 ))=∫(dx/(((x+(1/2))^2 +(3/4))^3 ))= =64∫(dx/(((2x+1)^2 ++3)^3 ))= [u=2x+1 → dx=(du/2)] =32∫(du/((u^2 +3)^3 )) [∫(du/((au^2 +b)^n ))=(u/(2b(n−1)(au^2 +b)^(n−1) ))+((2n−3)/(2b(n−1)))∫(du/((au^2 +b)^(n−1) ))] a=1; b=3; n=3 =32((u/(12(u^2 +3)^2 ))+(1/4)∫(du/((u^2 +3)^2 )))= a=1; b=3; n=2 =32((u/(12(u^2 +3)^2 ))+(1/4)((u/(6(u^2 +3)))+(1/6)∫(du/(u^2 +3))))= [v=((u(√3))/3) → du=(√3)dv] =32((u/(12(u^2 +3)^2 ))+(1/4)((u/(6(u^2 +3)))+((√3)/(18))∫(dv/(v^2 +1))))= =32((u/(12(u^2 +3)^2 ))+(1/4)((u/(6(u^2 +3)))+((√3)/(18))arctan(v)))= =32((u/(12(u^2 +3)^2 ))+(1/4)((u/(6(u^2 +3)))+((√3)/(18))arctan(((u(√3))/3))))= =((8u)/(3(u^2 +3)^2 ))+((4u)/(3(u^2 +3)))+((4(√3))/9)arctan(((u(√3))/3))= =((4u(u^2 +5))/(3(u^2 +3)^2 ))+((4(√3))/9)arctan(((u(√3))/3))= =((4(2x+1)((2x+1)^2 +5))/(3((2x+1)^2 +3)^2 ))+((4(√3))/9)arctan(((√3)/3)(2x+1))= =(((2x+1)(2x^2 +2x+3))/(6(x^2 +x+1)^2 ))+((4(√3))/9)arctan(((√3)/3)(2x+1))+C ∫_(−∞) ^∞ (dx/((x^2 +x+1)^3 ))=((4(√3))/9)π
$$\int\frac{{dx}}{\left({x}^{\mathrm{2}} +{x}+\mathrm{1}\right)^{\mathrm{3}} }=\int\frac{{dx}}{\left(\left({x}+\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} +\frac{\mathrm{3}}{\mathrm{4}}\right)^{\mathrm{3}} }= \\ $$$$=\mathrm{64}\int\frac{{dx}}{\left(\left(\mathrm{2}{x}+\mathrm{1}\right)^{\mathrm{2}} ++\mathrm{3}\right)^{\mathrm{3}} }= \\ $$$$\:\:\:\:\:\:\:\:\:\:\left[{u}=\mathrm{2}{x}+\mathrm{1}\:\rightarrow\:{dx}=\frac{{du}}{\mathrm{2}}\right] \\ $$$$=\mathrm{32}\int\frac{{du}}{\left({u}^{\mathrm{2}} +\mathrm{3}\right)^{\mathrm{3}} } \\ $$$$\:\:\:\:\:\:\:\:\:\:\left[\int\frac{{du}}{\left({au}^{\mathrm{2}} +{b}\right)^{{n}} }=\frac{{u}}{\mathrm{2}{b}\left({n}−\mathrm{1}\right)\left({au}^{\mathrm{2}} +{b}\right)^{{n}−\mathrm{1}} }+\frac{\mathrm{2}{n}−\mathrm{3}}{\mathrm{2}{b}\left({n}−\mathrm{1}\right)}\int\frac{{du}}{\left({au}^{\mathrm{2}} +{b}\right)^{{n}−\mathrm{1}} }\right] \\ $$$$\:\:\:\:\:{a}=\mathrm{1};\:{b}=\mathrm{3};\:{n}=\mathrm{3} \\ $$$$=\mathrm{32}\left(\frac{{u}}{\mathrm{12}\left({u}^{\mathrm{2}} +\mathrm{3}\right)^{\mathrm{2}} }+\frac{\mathrm{1}}{\mathrm{4}}\int\frac{{du}}{\left({u}^{\mathrm{2}} +\mathrm{3}\right)^{\mathrm{2}} }\right)= \\ $$$$\:\:\:\:\:{a}=\mathrm{1};\:{b}=\mathrm{3};\:{n}=\mathrm{2} \\ $$$$=\mathrm{32}\left(\frac{{u}}{\mathrm{12}\left({u}^{\mathrm{2}} +\mathrm{3}\right)^{\mathrm{2}} }+\frac{\mathrm{1}}{\mathrm{4}}\left(\frac{{u}}{\mathrm{6}\left({u}^{\mathrm{2}} +\mathrm{3}\right)}+\frac{\mathrm{1}}{\mathrm{6}}\int\frac{{du}}{{u}^{\mathrm{2}} +\mathrm{3}}\right)\right)= \\ $$$$\:\:\:\:\:\:\:\:\:\:\left[{v}=\frac{{u}\sqrt{\mathrm{3}}}{\mathrm{3}}\:\rightarrow\:{du}=\sqrt{\mathrm{3}}{dv}\right] \\ $$$$=\mathrm{32}\left(\frac{{u}}{\mathrm{12}\left({u}^{\mathrm{2}} +\mathrm{3}\right)^{\mathrm{2}} }+\frac{\mathrm{1}}{\mathrm{4}}\left(\frac{{u}}{\mathrm{6}\left({u}^{\mathrm{2}} +\mathrm{3}\right)}+\frac{\sqrt{\mathrm{3}}}{\mathrm{18}}\int\frac{{dv}}{{v}^{\mathrm{2}} +\mathrm{1}}\right)\right)= \\ $$$$=\mathrm{32}\left(\frac{{u}}{\mathrm{12}\left({u}^{\mathrm{2}} +\mathrm{3}\right)^{\mathrm{2}} }+\frac{\mathrm{1}}{\mathrm{4}}\left(\frac{{u}}{\mathrm{6}\left({u}^{\mathrm{2}} +\mathrm{3}\right)}+\frac{\sqrt{\mathrm{3}}}{\mathrm{18}}\mathrm{arctan}\left({v}\right)\right)\right)= \\ $$$$=\mathrm{32}\left(\frac{{u}}{\mathrm{12}\left({u}^{\mathrm{2}} +\mathrm{3}\right)^{\mathrm{2}} }+\frac{\mathrm{1}}{\mathrm{4}}\left(\frac{{u}}{\mathrm{6}\left({u}^{\mathrm{2}} +\mathrm{3}\right)}+\frac{\sqrt{\mathrm{3}}}{\mathrm{18}}\mathrm{arctan}\left(\frac{{u}\sqrt{\mathrm{3}}}{\mathrm{3}}\right)\right)\right)= \\ $$$$=\frac{\mathrm{8}{u}}{\mathrm{3}\left({u}^{\mathrm{2}} +\mathrm{3}\right)^{\mathrm{2}} }+\frac{\mathrm{4}{u}}{\mathrm{3}\left({u}^{\mathrm{2}} +\mathrm{3}\right)}+\frac{\mathrm{4}\sqrt{\mathrm{3}}}{\mathrm{9}}\mathrm{arctan}\left(\frac{{u}\sqrt{\mathrm{3}}}{\mathrm{3}}\right)= \\ $$$$=\frac{\mathrm{4}{u}\left({u}^{\mathrm{2}} +\mathrm{5}\right)}{\mathrm{3}\left({u}^{\mathrm{2}} +\mathrm{3}\right)^{\mathrm{2}} }+\frac{\mathrm{4}\sqrt{\mathrm{3}}}{\mathrm{9}}\mathrm{arctan}\left(\frac{{u}\sqrt{\mathrm{3}}}{\mathrm{3}}\right)= \\ $$$$=\frac{\mathrm{4}\left(\mathrm{2}{x}+\mathrm{1}\right)\left(\left(\mathrm{2}{x}+\mathrm{1}\right)^{\mathrm{2}} +\mathrm{5}\right)}{\mathrm{3}\left(\left(\mathrm{2}{x}+\mathrm{1}\right)^{\mathrm{2}} +\mathrm{3}\right)^{\mathrm{2}} }+\frac{\mathrm{4}\sqrt{\mathrm{3}}}{\mathrm{9}}\mathrm{arctan}\left(\frac{\sqrt{\mathrm{3}}}{\mathrm{3}}\left(\mathrm{2}{x}+\mathrm{1}\right)\right)= \\ $$$$=\frac{\left(\mathrm{2}{x}+\mathrm{1}\right)\left(\mathrm{2}{x}^{\mathrm{2}} +\mathrm{2}{x}+\mathrm{3}\right)}{\mathrm{6}\left({x}^{\mathrm{2}} +{x}+\mathrm{1}\right)^{\mathrm{2}} }+\frac{\mathrm{4}\sqrt{\mathrm{3}}}{\mathrm{9}}\mathrm{arctan}\left(\frac{\sqrt{\mathrm{3}}}{\mathrm{3}}\left(\mathrm{2}{x}+\mathrm{1}\right)\right)+{C} \\ $$$$ \\ $$$$\underset{−\infty} {\overset{\infty} {\int}}\frac{{dx}}{\left({x}^{\mathrm{2}} +{x}+\mathrm{1}\right)^{\mathrm{3}} }=\frac{\mathrm{4}\sqrt{\mathrm{3}}}{\mathrm{9}}\pi \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *