Menu Close

calculate-dx-x-1-3-x-2-3x-2-2-find-the-value-of-2-dx-x-1-3-x-2-3x-2-

Tinku Tara 0 Comments
Pin




Question Number 56939 by maxmathsup by imad last updated on 26/Mar/19
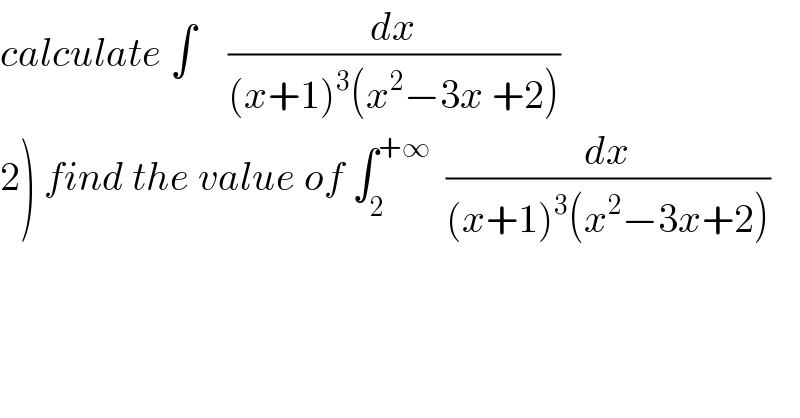
calculate ∫ (dx/((x+1)^3 (x^2 −3x +2))) 2) find the value of ∫_2 ^(+∞) (dx/((x+1)^3 (x^2 −3x+2)))
$${calculate}\:\int\:\:\:\:\frac{{dx}}{\left({x}+\mathrm{1}\right)^{\mathrm{3}} \left({x}^{\mathrm{2}} −\mathrm{3}{x}\:+\mathrm{2}\right)} \\ $$$$\left.\mathrm{2}\right)\:{find}\:{the}\:{value}\:{of}\:\int_{\mathrm{2}} ^{+\infty} \:\:\frac{{dx}}{\left({x}+\mathrm{1}\right)^{\mathrm{3}} \left({x}^{\mathrm{2}} −\mathrm{3}{x}+\mathrm{2}\right)} \\ $$
Commented by turbo msup by abdo last updated on 27/Mar/19
2)the question is find ∫_3 ^(+∞) (dx/((x+1)^2 (x^2 −3x +2)))
$$\left.\mathrm{2}\right){the}\:{question}\:{is}\:{find}\:\int_{\mathrm{3}} ^{+\infty} \:\frac{{dx}}{\left({x}+\mathrm{1}\right)^{\mathrm{2}} \left({x}^{\mathrm{2}} −\mathrm{3}{x}\:+\mathrm{2}\right)} \\ $$
Commented by maxmathsup by imad last updated on 27/Mar/19
changement x+1=t give I =∫ (dt/(t^3 ( (t−1)^2 −3(t−1) +2))) =∫ (dt/(t^3 (t^2 −2t +1−3t +3+2))) =∫ (dt/(t^3 ( t^2 −5t+6))) let decopose F(t)=(1/(t^3 (t^2 −5t +6))) roots of t^2 −5t +6 Δ=25−24=1 ⇒t_1 =((5+1)/2) =3 and t_2 =((5−1)/2) =2 ⇒ F(t)=(1/(t^3 (t−3)(t−2))) =(a/t) +(b/t^2 ) +(c/t^3 ) +(d/(t−3)) +(e/(t−2)) c=lim_(t→0) t^3 F(t)=(1/6) d =lim_(t→3) (t−3)F(t) =(1/(27)) e =lim_(t→2) (t−2)F(t)=−(1/8) ⇒F(t)=(a/t) +(b/t^2 ) +(1/(6t^3 )) +(1/(27(t−3))) −(1/(8(t−2))) lim_(t→+∞) tF(t)=0 =a +(1/(27)) −(1/8) =a+((8−27)/(27.8)) =a−((19)/(216)) ⇒a=((19)/(216)) ⇒ F(t)=((19)/(216t)) +(b/t^2 ) +(1/(6t^3 )) +(1/(27(t−3))) −(1/(8(t−2))) F(1)=(1/2) =((19)/(216)) +b +(1/6) −(1/(54)) +(1/8) ⇒1 =((19)/(108)) +2b +(1/3) −(1/(27)) +(1/4) =2b +((19)/(108)) +(7/(12)) −(1/(27)) ⇒2b =1−((19)/(108)) −(7/(12)) +(1/(27)) ⇒b=(1/2) −((19)/(216)) −(7/(24)) +(1/(54)) =b_0 ⇒ ∫F(t)dt =((19)/(216))ln∣t∣−(b_0 /t) +(1/6) (1/(−2)) t^(−2) +(1/(27))ln∣t−3∣−(1/8)ln∣t−2∣ +c =((19)/(216))ln∣t∣ −(b_0 /t) −(1/(12t^2 )) +(1/(27))ln∣t−3∣ −(1/8)ln∣t−2∣ +c =((19)/(216))ln∣x+1∣ −(b_0 /(x+1)) −(1/(12(x+1)^2 )) +(1/(27))ln∣x−2∣ −(1/8)ln∣x−1∣ +c =I .
$${changement}\:{x}+\mathrm{1}={t}\:{give}\:{I}\:=\int\:\:\frac{{dt}}{{t}^{\mathrm{3}} \left(\:\left({t}−\mathrm{1}\right)^{\mathrm{2}} −\mathrm{3}\left({t}−\mathrm{1}\right)\:+\mathrm{2}\right)} \\ $$$$=\int\:\:\:\:\frac{{dt}}{{t}^{\mathrm{3}} \left({t}^{\mathrm{2}} −\mathrm{2}{t}\:+\mathrm{1}−\mathrm{3}{t}\:+\mathrm{3}+\mathrm{2}\right)}\:=\int\:\:\:\:\frac{{dt}}{{t}^{\mathrm{3}} \left(\:{t}^{\mathrm{2}} \:−\mathrm{5}{t}+\mathrm{6}\right)}\:\:{let}\:{decopose} \\ $$$${F}\left({t}\right)=\frac{\mathrm{1}}{{t}^{\mathrm{3}} \left({t}^{\mathrm{2}} −\mathrm{5}{t}\:+\mathrm{6}\right)}\:\:\:\:\:{roots}\:{of}\:{t}^{\mathrm{2}} −\mathrm{5}{t}\:+\mathrm{6} \\ $$$$\Delta=\mathrm{25}−\mathrm{24}=\mathrm{1}\:\Rightarrow{t}_{\mathrm{1}} =\frac{\mathrm{5}+\mathrm{1}}{\mathrm{2}}\:=\mathrm{3}\:\:\:{and}\:\:{t}_{\mathrm{2}} =\frac{\mathrm{5}−\mathrm{1}}{\mathrm{2}}\:=\mathrm{2}\:\Rightarrow \\ $$$${F}\left({t}\right)=\frac{\mathrm{1}}{{t}^{\mathrm{3}} \left({t}−\mathrm{3}\right)\left({t}−\mathrm{2}\right)}\:=\frac{{a}}{{t}}\:+\frac{{b}}{{t}^{\mathrm{2}} }\:+\frac{{c}}{{t}^{\mathrm{3}} }\:+\frac{{d}}{{t}−\mathrm{3}}\:+\frac{{e}}{{t}−\mathrm{2}} \\ $$$${c}={lim}_{{t}\rightarrow\mathrm{0}} {t}^{\mathrm{3}} \:{F}\left({t}\right)=\frac{\mathrm{1}}{\mathrm{6}} \\ $$$${d}\:={lim}_{{t}\rightarrow\mathrm{3}} \left({t}−\mathrm{3}\right){F}\left({t}\right)\:=\frac{\mathrm{1}}{\mathrm{27}} \\ $$$${e}\:={lim}_{{t}\rightarrow\mathrm{2}} \left({t}−\mathrm{2}\right){F}\left({t}\right)=−\frac{\mathrm{1}}{\mathrm{8}}\:\Rightarrow{F}\left({t}\right)=\frac{{a}}{{t}}\:+\frac{{b}}{{t}^{\mathrm{2}} }\:+\frac{\mathrm{1}}{\mathrm{6}{t}^{\mathrm{3}} }\:+\frac{\mathrm{1}}{\mathrm{27}\left({t}−\mathrm{3}\right)}\:−\frac{\mathrm{1}}{\mathrm{8}\left({t}−\mathrm{2}\right)} \\ $$$${lim}_{{t}\rightarrow+\infty} {tF}\left({t}\right)=\mathrm{0}\:={a}\:+\frac{\mathrm{1}}{\mathrm{27}}\:−\frac{\mathrm{1}}{\mathrm{8}}\:={a}+\frac{\mathrm{8}−\mathrm{27}}{\mathrm{27}.\mathrm{8}}\:={a}−\frac{\mathrm{19}}{\mathrm{216}}\:\Rightarrow{a}=\frac{\mathrm{19}}{\mathrm{216}}\:\Rightarrow \\ $$$${F}\left({t}\right)=\frac{\mathrm{19}}{\mathrm{216}{t}}\:+\frac{{b}}{{t}^{\mathrm{2}} }\:+\frac{\mathrm{1}}{\mathrm{6}{t}^{\mathrm{3}} }\:+\frac{\mathrm{1}}{\mathrm{27}\left({t}−\mathrm{3}\right)}\:−\frac{\mathrm{1}}{\mathrm{8}\left({t}−\mathrm{2}\right)} \\ $$$${F}\left(\mathrm{1}\right)=\frac{\mathrm{1}}{\mathrm{2}}\:=\frac{\mathrm{19}}{\mathrm{216}}\:+{b}\:+\frac{\mathrm{1}}{\mathrm{6}}\:−\frac{\mathrm{1}}{\mathrm{54}}\:+\frac{\mathrm{1}}{\mathrm{8}}\:\Rightarrow\mathrm{1}\:=\frac{\mathrm{19}}{\mathrm{108}}\:+\mathrm{2}{b}\:+\frac{\mathrm{1}}{\mathrm{3}}\:−\frac{\mathrm{1}}{\mathrm{27}}\:+\frac{\mathrm{1}}{\mathrm{4}} \\ $$$$=\mathrm{2}{b}\:+\frac{\mathrm{19}}{\mathrm{108}}\:+\frac{\mathrm{7}}{\mathrm{12}}\:−\frac{\mathrm{1}}{\mathrm{27}}\:\Rightarrow\mathrm{2}{b}\:=\mathrm{1}−\frac{\mathrm{19}}{\mathrm{108}}\:−\frac{\mathrm{7}}{\mathrm{12}}\:+\frac{\mathrm{1}}{\mathrm{27}}\:\Rightarrow{b}=\frac{\mathrm{1}}{\mathrm{2}}\:−\frac{\mathrm{19}}{\mathrm{216}}\:−\frac{\mathrm{7}}{\mathrm{24}}\:+\frac{\mathrm{1}}{\mathrm{54}}\:={b}_{\mathrm{0}} \Rightarrow \\ $$$$\int{F}\left({t}\right){dt}\:=\frac{\mathrm{19}}{\mathrm{216}}{ln}\mid{t}\mid−\frac{{b}_{\mathrm{0}} }{{t}}\:\:+\frac{\mathrm{1}}{\mathrm{6}}\:\frac{\mathrm{1}}{−\mathrm{2}}\:{t}^{−\mathrm{2}} \:\:+\frac{\mathrm{1}}{\mathrm{27}}{ln}\mid{t}−\mathrm{3}\mid−\frac{\mathrm{1}}{\mathrm{8}}{ln}\mid{t}−\mathrm{2}\mid\:+{c} \\ $$$$=\frac{\mathrm{19}}{\mathrm{216}}{ln}\mid{t}\mid\:−\frac{{b}_{\mathrm{0}} }{{t}}\:−\frac{\mathrm{1}}{\mathrm{12}{t}^{\mathrm{2}} }\:+\frac{\mathrm{1}}{\mathrm{27}}{ln}\mid{t}−\mathrm{3}\mid\:−\frac{\mathrm{1}}{\mathrm{8}}{ln}\mid{t}−\mathrm{2}\mid\:+{c} \\ $$$$=\frac{\mathrm{19}}{\mathrm{216}}{ln}\mid{x}+\mathrm{1}\mid\:−\frac{{b}_{\mathrm{0}} }{{x}+\mathrm{1}}\:−\frac{\mathrm{1}}{\mathrm{12}\left({x}+\mathrm{1}\right)^{\mathrm{2}} }\:+\frac{\mathrm{1}}{\mathrm{27}}{ln}\mid{x}−\mathrm{2}\mid\:−\frac{\mathrm{1}}{\mathrm{8}}{ln}\mid{x}−\mathrm{1}\mid\:+{c}\:={I}\:. \\ $$$$ \\ $$
Answered by MJS last updated on 27/Mar/19
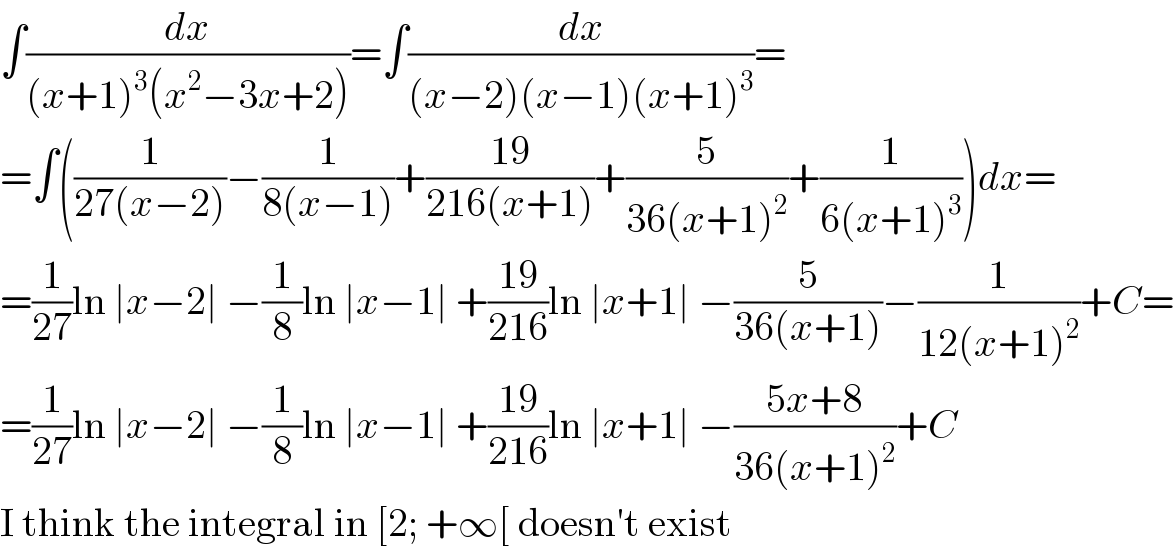
∫(dx/((x+1)^3 (x^2 −3x+2)))=∫(dx/((x−2)(x−1)(x+1)^3 ))= =∫((1/(27(x−2)))−(1/(8(x−1)))+((19)/(216(x+1)))+(5/(36(x+1)^2 ))+(1/(6(x+1)^3 )))dx= =(1/(27))ln ∣x−2∣ −(1/8)ln ∣x−1∣ +((19)/(216))ln ∣x+1∣ −(5/(36(x+1)))−(1/(12(x+1)^2 ))+C= =(1/(27))ln ∣x−2∣ −(1/8)ln ∣x−1∣ +((19)/(216))ln ∣x+1∣ −((5x+8)/(36(x+1)^2 ))+C I think the integral in [2; +∞[ doesn′t exist
$$\int\frac{{dx}}{\left({x}+\mathrm{1}\right)^{\mathrm{3}} \left({x}^{\mathrm{2}} −\mathrm{3}{x}+\mathrm{2}\right)}=\int\frac{{dx}}{\left({x}−\mathrm{2}\right)\left({x}−\mathrm{1}\right)\left({x}+\mathrm{1}\right)^{\mathrm{3}} }= \\ $$$$=\int\left(\frac{\mathrm{1}}{\mathrm{27}\left({x}−\mathrm{2}\right)}−\frac{\mathrm{1}}{\mathrm{8}\left({x}−\mathrm{1}\right)}+\frac{\mathrm{19}}{\mathrm{216}\left({x}+\mathrm{1}\right)}+\frac{\mathrm{5}}{\mathrm{36}\left({x}+\mathrm{1}\right)^{\mathrm{2}} }+\frac{\mathrm{1}}{\mathrm{6}\left({x}+\mathrm{1}\right)^{\mathrm{3}} }\right){dx}= \\ $$$$=\frac{\mathrm{1}}{\mathrm{27}}\mathrm{ln}\:\mid{x}−\mathrm{2}\mid\:−\frac{\mathrm{1}}{\mathrm{8}}\mathrm{ln}\:\mid{x}−\mathrm{1}\mid\:+\frac{\mathrm{19}}{\mathrm{216}}\mathrm{ln}\:\mid{x}+\mathrm{1}\mid\:−\frac{\mathrm{5}}{\mathrm{36}\left({x}+\mathrm{1}\right)}−\frac{\mathrm{1}}{\mathrm{12}\left({x}+\mathrm{1}\right)^{\mathrm{2}} }+{C}= \\ $$$$=\frac{\mathrm{1}}{\mathrm{27}}\mathrm{ln}\:\mid{x}−\mathrm{2}\mid\:−\frac{\mathrm{1}}{\mathrm{8}}\mathrm{ln}\:\mid{x}−\mathrm{1}\mid\:+\frac{\mathrm{19}}{\mathrm{216}}\mathrm{ln}\:\mid{x}+\mathrm{1}\mid\:−\frac{\mathrm{5}{x}+\mathrm{8}}{\mathrm{36}\left({x}+\mathrm{1}\right)^{\mathrm{2}} }+{C} \\ $$$$\mathrm{I}\:\mathrm{think}\:\mathrm{the}\:\mathrm{integral}\:\mathrm{in}\:\left[\mathrm{2};\:+\infty\left[\:\mathrm{doesn}'\mathrm{t}\:\mathrm{exist}\right.\right. \\ $$
Commented by turbo msup by abdo last updated on 27/Mar/19
thank you sir.
$${thank}\:{you}\:{sir}. \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *