Menu Close

calculate-dx-x-2-1-2-x-2-9-2-

Tinku Tara 0 Comments
Pin




Question Number 102158 by mathmax by abdo last updated on 07/Jul/20
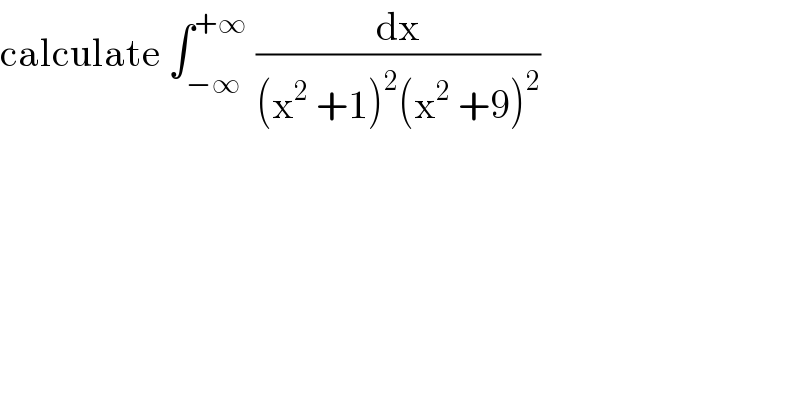
calculate ∫_(−∞) ^(+∞) (dx/((x^2 +1)^2 (x^2 +9)^2 ))
$$\mathrm{calculate}\:\int_{−\infty} ^{+\infty} \:\frac{\mathrm{dx}}{\left(\mathrm{x}^{\mathrm{2}} \:+\mathrm{1}\right)^{\mathrm{2}} \left(\mathrm{x}^{\mathrm{2}} \:+\mathrm{9}\right)^{\mathrm{2}} } \\ $$
Answered by mathmax by abdo last updated on 09/Jul/20
I =∫_(−∞) ^(+∞) (dx/((x^2 +1)^2 (x^2 +9)^2 )) let ϕ(z)=(1/((z^2 +1)^2 (z^2 +9)^2 )) we have ϕ(z) =(1/((z−i)^2 (z+i)^2 (z−3i)^2 (z+3i)^2 )) the poles of ϕ are +^− i and +^− 3i ∫_(−∞) ^(+∞) ϕ(z)dz =2iπ { Res(ϕ,i)+Res(ϕ,3i)} Res(ϕ,i) =lim_(z→i) (1/((2−1)!)){(z−i)^2 ϕ(z)}^((1)) lim_(z→i) {(1/((z+i)^2 (z^2 +9)^2 ))}^((1)) =lim_(z→i) −((2(z+i)(z^2 +9)^2 +2(2z)(z^2 +9)(z+i)^2 )/((z+i)^4 (z^2 +9)^4 )) =−lim_(z→i) ((2(z^2 +9)+4z(z+i))/((z+i)^3 (z^2 +9)^3 )) =−((2×8+4i(2i))/((2i)^3 ×8^3 )) =−(8/(−8i×8^3 )) =(1/(8^3 i)) Res(ϕ,3i) =lim_(z→3i) (1/((2−1)!)){(z−3i)^2 ϕ(z)}^((1)) =lim_(z→3i) {(1/((z^2 +1)^2 (z+3i)^2 ))}^((1)) =−lim_(z→3i) ((2(2z)(z^2 +1)(z+3i)^2 +2(z+3i)(z^2 +1)^2 )/((z^2 +1)^4 (z +3i)^4 )) =−lim_(z→3i) ((4z(z+3i) +2(z^2 +1))/((z^2 +1)^3 (z+3i)^3 )) =−((12i(6i)+2(−8))/((−8)^3 (6i)^3 )) =−((−12×6−16)/(−8^3 ×6^3 (−i))) =−((12×6 +16)/(8^3 ×6^3 i)) =−((72+16)/(48^3 i)) =−((88)/(48^3 i)) ⇒ ∫_(−∞) ^(+∞) ϕ(z)dz =2iπ{(1/(8^3 i))−((88)/(48^3 i))} =2π{ (1/8^3 ) −((88)/(48^3 ))} =I
$$\mathrm{I}\:=\int_{−\infty} ^{+\infty} \:\frac{\mathrm{dx}}{\left(\mathrm{x}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} \left(\mathrm{x}^{\mathrm{2}} \:+\mathrm{9}\right)^{\mathrm{2}} }\:\:\:\mathrm{let}\:\varphi\left(\mathrm{z}\right)=\frac{\mathrm{1}}{\left(\mathrm{z}^{\mathrm{2}} \:+\mathrm{1}\right)^{\mathrm{2}} \left(\mathrm{z}^{\mathrm{2}} \:+\mathrm{9}\right)^{\mathrm{2}} }\:\:\mathrm{we}\:\mathrm{have} \\ $$$$\varphi\left(\mathrm{z}\right)\:=\frac{\mathrm{1}}{\left(\mathrm{z}−\mathrm{i}\right)^{\mathrm{2}} \left(\mathrm{z}+\mathrm{i}\right)^{\mathrm{2}} \left(\mathrm{z}−\mathrm{3i}\right)^{\mathrm{2}} \left(\mathrm{z}+\mathrm{3i}\right)^{\mathrm{2}} }\:\mathrm{the}\:\mathrm{poles}\:\mathrm{of}\:\varphi\:\mathrm{are}\:\overset{−} {+}\mathrm{i}\:\mathrm{and}\:\overset{−} {+}\mathrm{3i} \\ $$$$\int_{−\infty} ^{+\infty} \varphi\left(\mathrm{z}\right)\mathrm{dz}\:=\mathrm{2i}\pi\:\left\{\:\mathrm{Res}\left(\varphi,\mathrm{i}\right)+\mathrm{Res}\left(\varphi,\mathrm{3i}\right)\right\} \\ $$$$\mathrm{Res}\left(\varphi,\mathrm{i}\right)\:=\mathrm{lim}_{\mathrm{z}\rightarrow\mathrm{i}} \:\:\:\frac{\mathrm{1}}{\left(\mathrm{2}−\mathrm{1}\right)!}\left\{\left(\mathrm{z}−\mathrm{i}\right)^{\mathrm{2}} \varphi\left(\mathrm{z}\right)\right\}^{\left(\mathrm{1}\right)} \\ $$$$\mathrm{lim}_{\mathrm{z}\rightarrow\mathrm{i}} \:\:\:\:\left\{\frac{\mathrm{1}}{\left(\mathrm{z}+\mathrm{i}\right)^{\mathrm{2}} \left(\mathrm{z}^{\mathrm{2}} \:+\mathrm{9}\right)^{\mathrm{2}} }\right\}^{\left(\mathrm{1}\right)} \\ $$$$=\mathrm{lim}_{\mathrm{z}\rightarrow\mathrm{i}} \:\:\:−\frac{\mathrm{2}\left(\mathrm{z}+\mathrm{i}\right)\left(\mathrm{z}^{\mathrm{2}} \:+\mathrm{9}\right)^{\mathrm{2}} \:+\mathrm{2}\left(\mathrm{2z}\right)\left(\mathrm{z}^{\mathrm{2}} \:+\mathrm{9}\right)\left(\mathrm{z}+\mathrm{i}\right)^{\mathrm{2}} }{\left(\mathrm{z}+\mathrm{i}\right)^{\mathrm{4}} \left(\mathrm{z}^{\mathrm{2}} +\mathrm{9}\right)^{\mathrm{4}} } \\ $$$$=−\mathrm{lim}_{\mathrm{z}\rightarrow\mathrm{i}} \:\:\frac{\mathrm{2}\left(\mathrm{z}^{\mathrm{2}} \:+\mathrm{9}\right)+\mathrm{4z}\left(\mathrm{z}+\mathrm{i}\right)}{\left(\mathrm{z}+\mathrm{i}\right)^{\mathrm{3}} \left(\mathrm{z}^{\mathrm{2}} \:+\mathrm{9}\right)^{\mathrm{3}} }\:=−\frac{\mathrm{2}×\mathrm{8}+\mathrm{4i}\left(\mathrm{2i}\right)}{\left(\mathrm{2i}\right)^{\mathrm{3}} ×\mathrm{8}^{\mathrm{3}} }\:=−\frac{\mathrm{8}}{−\mathrm{8i}×\mathrm{8}^{\mathrm{3}} }\:=\frac{\mathrm{1}}{\mathrm{8}^{\mathrm{3}} \mathrm{i}} \\ $$$$\mathrm{Res}\left(\varphi,\mathrm{3i}\right)\:=\mathrm{lim}_{\mathrm{z}\rightarrow\mathrm{3i}} \:\frac{\mathrm{1}}{\left(\mathrm{2}−\mathrm{1}\right)!}\left\{\left(\mathrm{z}−\mathrm{3i}\right)^{\mathrm{2}} \varphi\left(\mathrm{z}\right)\right\}^{\left(\mathrm{1}\right)} \\ $$$$=\mathrm{lim}_{\mathrm{z}\rightarrow\mathrm{3i}} \:\:\:\:\left\{\frac{\mathrm{1}}{\left(\mathrm{z}^{\mathrm{2}} \:+\mathrm{1}\right)^{\mathrm{2}} \left(\mathrm{z}+\mathrm{3i}\right)^{\mathrm{2}} }\right\}^{\left(\mathrm{1}\right)} \\ $$$$=−\mathrm{lim}_{\mathrm{z}\rightarrow\mathrm{3i}} \:\:\:\frac{\mathrm{2}\left(\mathrm{2z}\right)\left(\mathrm{z}^{\mathrm{2}} \:+\mathrm{1}\right)\left(\mathrm{z}+\mathrm{3i}\right)^{\mathrm{2}} \:+\mathrm{2}\left(\mathrm{z}+\mathrm{3i}\right)\left(\mathrm{z}^{\mathrm{2}} \:+\mathrm{1}\right)^{\mathrm{2}} }{\left(\mathrm{z}^{\mathrm{2}} \:+\mathrm{1}\right)^{\mathrm{4}} \left(\mathrm{z}\:+\mathrm{3i}\right)^{\mathrm{4}} } \\ $$$$=−\mathrm{lim}_{\mathrm{z}\rightarrow\mathrm{3i}} \:\:\:\frac{\mathrm{4z}\left(\mathrm{z}+\mathrm{3i}\right)\:+\mathrm{2}\left(\mathrm{z}^{\mathrm{2}} \:+\mathrm{1}\right)}{\left(\mathrm{z}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{3}} \left(\mathrm{z}+\mathrm{3i}\right)^{\mathrm{3}} }\:=−\frac{\mathrm{12i}\left(\mathrm{6i}\right)+\mathrm{2}\left(−\mathrm{8}\right)}{\left(−\mathrm{8}\right)^{\mathrm{3}} \left(\mathrm{6i}\right)^{\mathrm{3}} } \\ $$$$=−\frac{−\mathrm{12}×\mathrm{6}−\mathrm{16}}{−\mathrm{8}^{\mathrm{3}} \:×\mathrm{6}^{\mathrm{3}} \left(−\mathrm{i}\right)}\:=−\frac{\mathrm{12}×\mathrm{6}\:+\mathrm{16}}{\mathrm{8}^{\mathrm{3}} \:×\mathrm{6}^{\mathrm{3}} \mathrm{i}}\:=−\frac{\mathrm{72}+\mathrm{16}}{\mathrm{48}^{\mathrm{3}} \mathrm{i}}\:=−\frac{\mathrm{88}}{\mathrm{48}^{\mathrm{3}} \mathrm{i}}\:\Rightarrow \\ $$$$\int_{−\infty} ^{+\infty} \:\varphi\left(\mathrm{z}\right)\mathrm{dz}\:=\mathrm{2i}\pi\left\{\frac{\mathrm{1}}{\mathrm{8}^{\mathrm{3}} \mathrm{i}}−\frac{\mathrm{88}}{\mathrm{48}^{\mathrm{3}} \mathrm{i}}\right\}\:=\mathrm{2}\pi\left\{\:\frac{\mathrm{1}}{\mathrm{8}^{\mathrm{3}} }\:−\frac{\mathrm{88}}{\mathrm{48}^{\mathrm{3}} }\right\}\:=\mathrm{I} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *