Question Number 34320 by abdo mathsup 649 cc last updated on 04/May/18
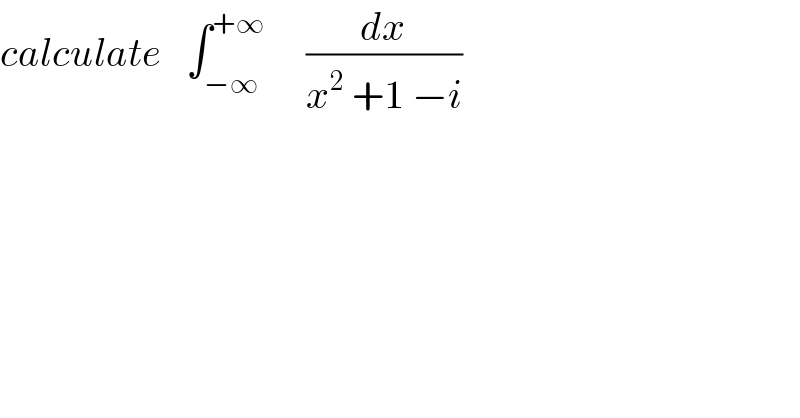
$${calculate}\:\:\:\int_{−\infty} ^{+\infty} \:\:\:\:\:\frac{{dx}}{{x}^{\mathrm{2}} \:+\mathrm{1}\:−{i}} \\ $$
Commented by math khazana by abdo last updated on 05/May/18
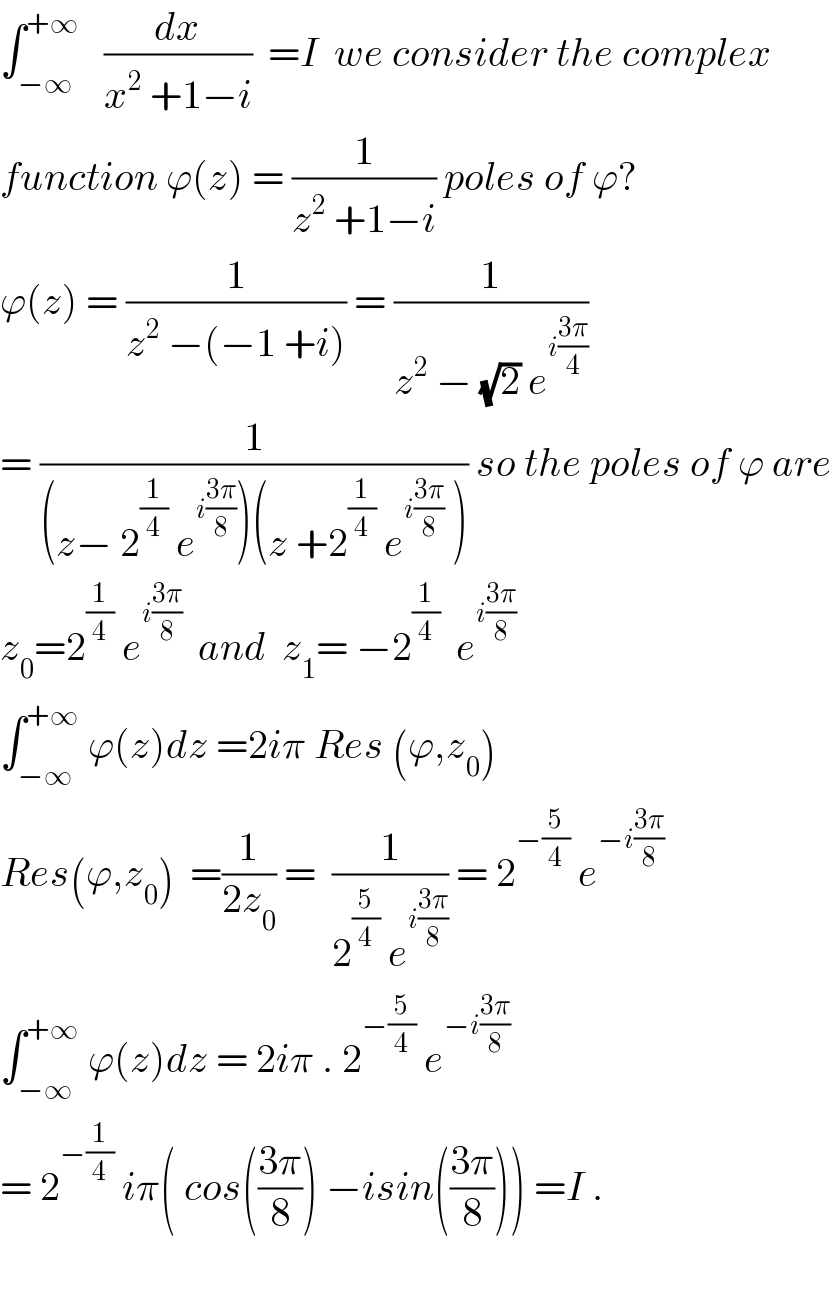
$$\int_{−\infty} ^{+\infty} \:\:\:\frac{{dx}}{{x}^{\mathrm{2}} \:+\mathrm{1}−{i}}\:\:={I}\:\:{we}\:{consider}\:{the}\:{complex} \\ $$$${function}\:\varphi\left({z}\right)\:=\:\frac{\mathrm{1}}{{z}^{\mathrm{2}} \:+\mathrm{1}−{i}}\:{poles}\:{of}\:\varphi? \\ $$$$\varphi\left({z}\right)\:=\:\frac{\mathrm{1}}{{z}^{\mathrm{2}} \:−\left(−\mathrm{1}\:+{i}\right)}\:=\:\frac{\mathrm{1}}{{z}^{\mathrm{2}} \:−\:\sqrt{\mathrm{2}}\:{e}^{{i}\frac{\mathrm{3}\pi}{\mathrm{4}}} } \\ $$$$=\:\frac{\mathrm{1}}{\left({z}−\:\mathrm{2}^{\frac{\mathrm{1}}{\mathrm{4}}} \:{e}^{{i}\frac{\mathrm{3}\pi}{\mathrm{8}}} \right)\left({z}\:+\mathrm{2}^{\frac{\mathrm{1}}{\mathrm{4}}} \:{e}^{{i}\frac{\mathrm{3}\pi}{\mathrm{8}}} \:\right)}\:{so}\:{the}\:{poles}\:{of}\:\varphi\:{are} \\ $$$${z}_{\mathrm{0}} =\mathrm{2}^{\frac{\mathrm{1}}{\mathrm{4}}} \:{e}^{{i}\frac{\mathrm{3}\pi}{\mathrm{8}}} \:\:{and}\:\:{z}_{\mathrm{1}} =\:−\mathrm{2}^{\frac{\mathrm{1}}{\mathrm{4}}} \:\:{e}^{{i}\frac{\mathrm{3}\pi}{\mathrm{8}}} \\ $$$$\int_{−\infty} ^{+\infty} \:\varphi\left({z}\right){dz}\:=\mathrm{2}{i}\pi\:{Res}\:\left(\varphi,{z}_{\mathrm{0}} \right) \\ $$$${Res}\left(\varphi,{z}_{\mathrm{0}} \right)\:\:=\frac{\mathrm{1}}{\mathrm{2}{z}_{\mathrm{0}} }\:=\:\:\frac{\mathrm{1}}{\mathrm{2}^{\frac{\mathrm{5}}{\mathrm{4}}} \:{e}^{{i}\frac{\mathrm{3}\pi}{\mathrm{8}}} }\:=\:\mathrm{2}^{−\frac{\mathrm{5}}{\mathrm{4}}} \:{e}^{−{i}\frac{\mathrm{3}\pi}{\mathrm{8}}} \\ $$$$\int_{−\infty} ^{+\infty} \:\varphi\left({z}\right){dz}\:=\:\mathrm{2}{i}\pi\:.\:\mathrm{2}^{−\frac{\mathrm{5}}{\mathrm{4}}} \:{e}^{−{i}\frac{\mathrm{3}\pi}{\mathrm{8}}} \\ $$$$=\:\mathrm{2}^{−\frac{\mathrm{1}}{\mathrm{4}}} \:{i}\pi\left(\:{cos}\left(\frac{\mathrm{3}\pi}{\mathrm{8}}\right)\:−{isin}\left(\frac{\mathrm{3}\pi}{\mathrm{8}}\right)\right)\:={I}\:. \\ $$$$ \\ $$
Commented by math khazana by abdo last updated on 05/May/18
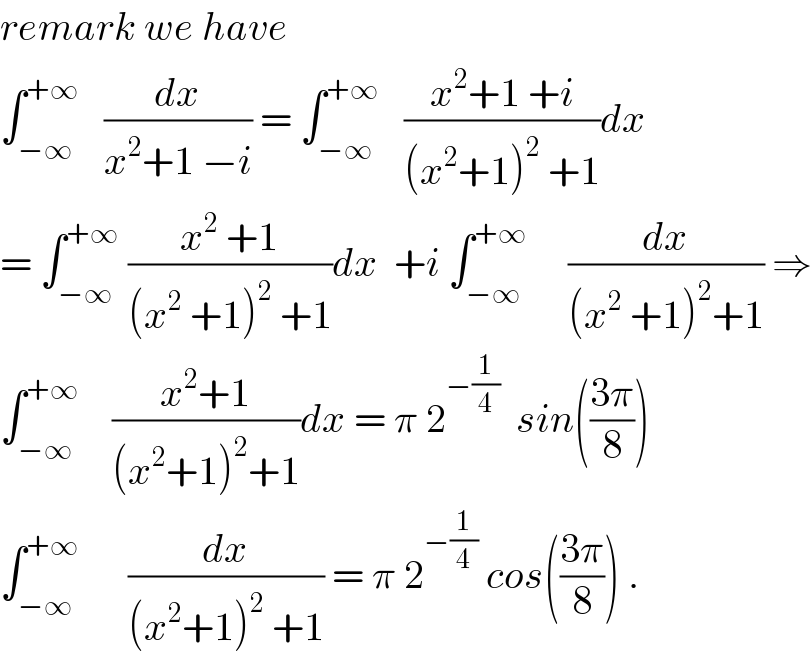
$${remark}\:{we}\:{have} \\ $$$$\int_{−\infty} ^{+\infty} \:\:\:\frac{{dx}}{{x}^{\mathrm{2}} +\mathrm{1}\:−{i}}\:=\:\int_{−\infty} ^{+\infty} \:\:\:\frac{{x}^{\mathrm{2}} +\mathrm{1}\:+{i}}{\left({x}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} \:+\mathrm{1}}{dx} \\ $$$$=\:\int_{−\infty} ^{+\infty} \:\frac{{x}^{\mathrm{2}} \:+\mathrm{1}}{\left({x}^{\mathrm{2}} \:+\mathrm{1}\right)^{\mathrm{2}} \:+\mathrm{1}}{dx}\:\:+{i}\:\int_{−\infty} ^{+\infty} \:\:\:\:\:\frac{{dx}}{\left({x}^{\mathrm{2}} \:+\mathrm{1}\right)^{\mathrm{2}} +\mathrm{1}}\:\Rightarrow \\ $$$$\int_{−\infty} ^{+\infty} \:\:\:\:\frac{{x}^{\mathrm{2}} +\mathrm{1}}{\left({x}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} +\mathrm{1}}{dx}\:=\:\pi\:\mathrm{2}^{−\frac{\mathrm{1}}{\mathrm{4}}} \:\:{sin}\left(\frac{\mathrm{3}\pi}{\mathrm{8}}\right) \\ $$$$\int_{−\infty} ^{+\infty} \:\:\:\:\:\:\frac{{dx}}{\left({x}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} \:+\mathrm{1}}\:=\:\pi\:\mathrm{2}^{−\frac{\mathrm{1}}{\mathrm{4}}} \:{cos}\left(\frac{\mathrm{3}\pi}{\mathrm{8}}\right)\:. \\ $$
