Question Number 42708 by prof Abdo imad last updated on 01/Sep/18
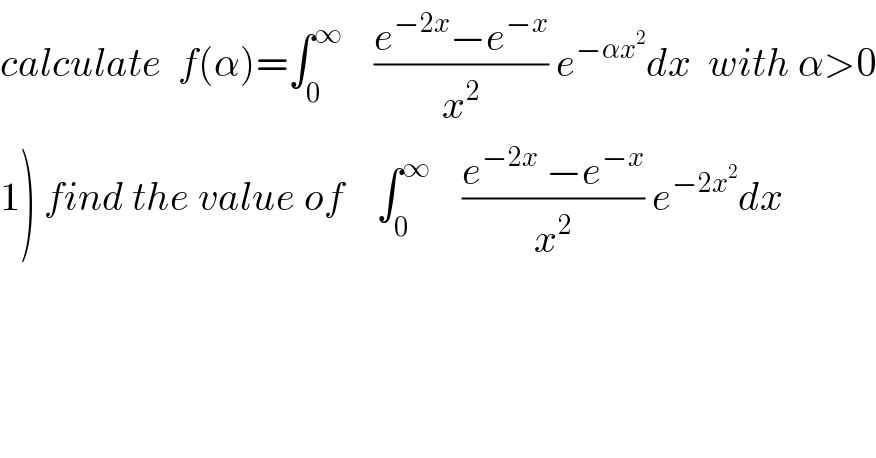
$${calculate}\:\:{f}\left(\alpha\right)=\int_{\mathrm{0}} ^{\infty} \:\:\:\:\frac{{e}^{−\mathrm{2}{x}} −{e}^{−{x}} }{{x}^{\mathrm{2}} }\:{e}^{−\alpha{x}^{\mathrm{2}} } {dx}\:\:{with}\:\alpha>\mathrm{0} \\ $$$$\left.\mathrm{1}\right)\:{find}\:{the}\:{value}\:{of}\:\:\:\:\int_{\mathrm{0}} ^{\infty} \:\:\:\:\frac{{e}^{−\mathrm{2}{x}} \:−{e}^{−{x}} }{{x}^{\mathrm{2}} }\:{e}^{−\mathrm{2}{x}^{\mathrm{2}} } {dx} \\ $$
Commented by maxmathsup by imad last updated on 02/Sep/18

$$\left.\mathrm{1}\right)\:{f}^{'} \left(\alpha\right)\:=\:−\int_{\mathrm{0}} ^{+\infty} \:\:\left({e}^{−\mathrm{2}{x}} −{e}^{−{x}} \right){e}^{−\alpha{x}^{\mathrm{2}} } {dx}\:=\int_{\mathrm{0}} ^{\infty} \:\:{e}^{−\alpha{x}^{\mathrm{2}} −{x}} {dx}\:−\int_{\mathrm{0}} ^{\infty} \:{e}^{−\alpha{x}^{\mathrm{2}} −\mathrm{2}{x}} {dx} \\ $$$${but}\:\int_{\mathrm{0}} ^{\infty} \:\:\:{e}^{−\alpha{x}^{\mathrm{2}} −{x}} {dx}\:=\int_{\mathrm{0}} ^{\infty} \:\:\:\:{e}^{−\left\{\left(\sqrt{\alpha}{x}\right)^{\mathrm{2}} \:\:+\mathrm{2}\:\frac{\sqrt{\alpha}{x}}{\mathrm{2}\sqrt{\alpha}}\:\:\:+\:\frac{\mathrm{1}}{\mathrm{4}\alpha}−\frac{\mathrm{1}}{\mathrm{4}\alpha}\right)} {dx}\:=\int_{\mathrm{0}} ^{\infty} \:\:{e}^{−\left\{\left(\sqrt{\alpha}{x}\:+\frac{\mathrm{1}}{\mathrm{2}\sqrt{\alpha}}\right)^{\mathrm{2}} \right\}\:+\frac{\mathrm{1}}{\mathrm{4}\alpha}} \:{dx} \\ $$$$\:=_{\sqrt{\alpha}{x}\:\:+\frac{\mathrm{1}}{\mathrm{2}\sqrt{\alpha}}\:={t}} \:\:\:\:\:{e}^{\frac{\mathrm{1}}{\mathrm{4}\alpha}} \:\int_{\mathrm{0}} ^{\infty} \:\:\:\:{e}^{−{t}^{\mathrm{2}} \:\:\:} \:\frac{{dt}}{\:\sqrt{\alpha}}\:=\frac{\sqrt{\pi}}{\mathrm{2}}\:\:\:\frac{{e}^{\frac{\mathrm{1}}{\mathrm{4}\alpha}} }{\:\sqrt{\alpha}}\:\Rightarrow\:{f}\left(\alpha\right)\:=\:\int_{.} ^{\alpha} \:\frac{\sqrt{\pi}}{\mathrm{2}}\:\frac{{e}^{\frac{\mathrm{1}}{\mathrm{4}{x}}} }{\:\sqrt{{x}}}{dx}\:+{c} \\ $$$$=_{\sqrt{{x}}={u}} \:\:\:\frac{\sqrt{\pi}}{\mathrm{2}}\:\:\int_{.} ^{\sqrt{\alpha}} \:\frac{{e}^{\frac{\mathrm{1}}{\mathrm{4}{u}^{\mathrm{2}} }} }{{u}}\left(\mathrm{2}{u}\right){du}\:+{c}\:=\:\sqrt{\pi}\:\int_{.} ^{\sqrt{\alpha}} \:{e}^{\frac{\mathrm{1}}{\mathrm{4}{u}^{\mathrm{2}} }} \:{du}\:+{c}\:\Rightarrow{f}\left(\alpha\right)\:=\sqrt{\pi}\:\int_{\mathrm{1}} ^{\sqrt{\alpha}} \:{e}^{\frac{\mathrm{1}}{\mathrm{4}{u}^{\mathrm{2}} }} \:\:+{c} \\ $$$${c}\:={f}\left(\mathrm{1}\right)\:=\:\int_{\mathrm{0}} ^{\infty} \:\:\frac{{e}^{−{x}^{\mathrm{2}} −\mathrm{2}{x}} −{e}^{−{x}^{\mathrm{2}} −{x}} }{{x}^{\mathrm{2}} }{dx} \\ $$$$\left.\mathrm{2}\right)\:\int_{\mathrm{0}} ^{\infty} \:\:\:\frac{{e}^{−\mathrm{2}{x}} \:−{e}^{−{x}} }{{x}^{\mathrm{2}} }\:{e}^{−\mathrm{2}{x}^{\mathrm{2}} } {dx}\:={f}\left(\mathrm{2}\right)\:=\:\sqrt{\pi}\:\int_{\mathrm{1}} ^{\sqrt{\mathrm{2}}} \:{e}^{\frac{\mathrm{1}}{\mathrm{4}{u}^{\mathrm{2}} }} \:{du}\:\:+{f}\left(\mathrm{1}\right)\:…. \\ $$
